初中数学北师大版（2024）九年级上册第四章 图形的相似8 图形的位似综合训练题

这是一份初中数学北师大版（2024）九年级上册第四章 图形的相似8 图形的位似综合训练题，共23页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．（2024·山西大同·一模）下列选项中的两个相似图形，不是位似图形的是（ ）
A． B． C． D．
2．（23-24九年级下·河北沧州·期中）如图，在正方形网格图中，与是位似图形，则位似中心是（ ）
A．点RB．点PC．点QD．点O
3．（23-24九年级上·重庆·开学考试）如图，与是位似图形，相似比为，已知，则的长为（ ）
A．6B．8C．18D．20
4．（23-24八年级下·重庆江北·期末）如图，是以点为位似中心经过位似变换得到的，若，则的周长与的周长比是（ ）
A．B．C．D．
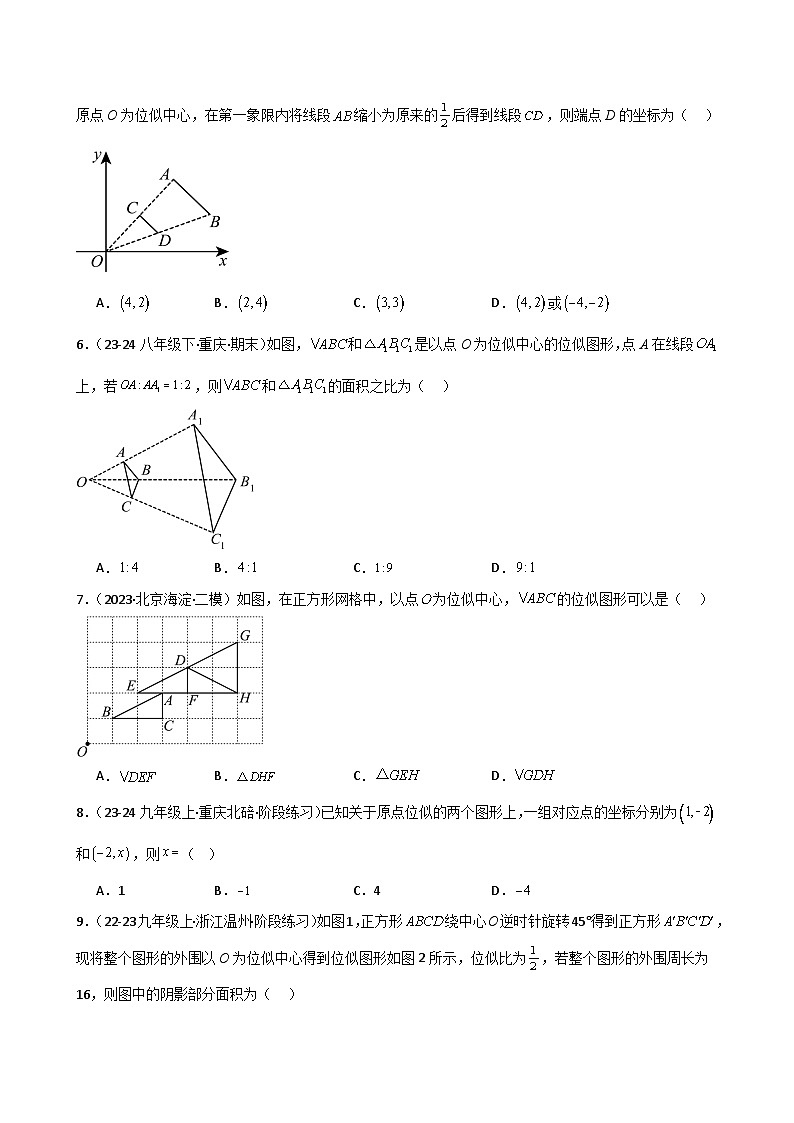
5．（23-24九年级上·山东青岛·阶段练习）如图，已知线段两个端点的坐标分别为，以原点O为位似中心，在第一象限内将线段缩小为原来的后得到线段，则端点D的坐标为（ ）
A．B．C．D．或
6．（23-24八年级下·重庆·期末）如图，和是以点O为位似中心的位似图形，点A在线段上，若，则和的面积之比为（ ）
A．B．C．D．
7．（2023·北京海淀·二模）如图，在正方形网格中，以点为位似中心，的位似图形可以是（ ）

A．B．C．D．
8．（23-24九年级上·重庆北碚·阶段练习）已知关于原点位似的两个图形上，一组对应点的坐标分别为和，则（ ）
A．1B．C．4D．
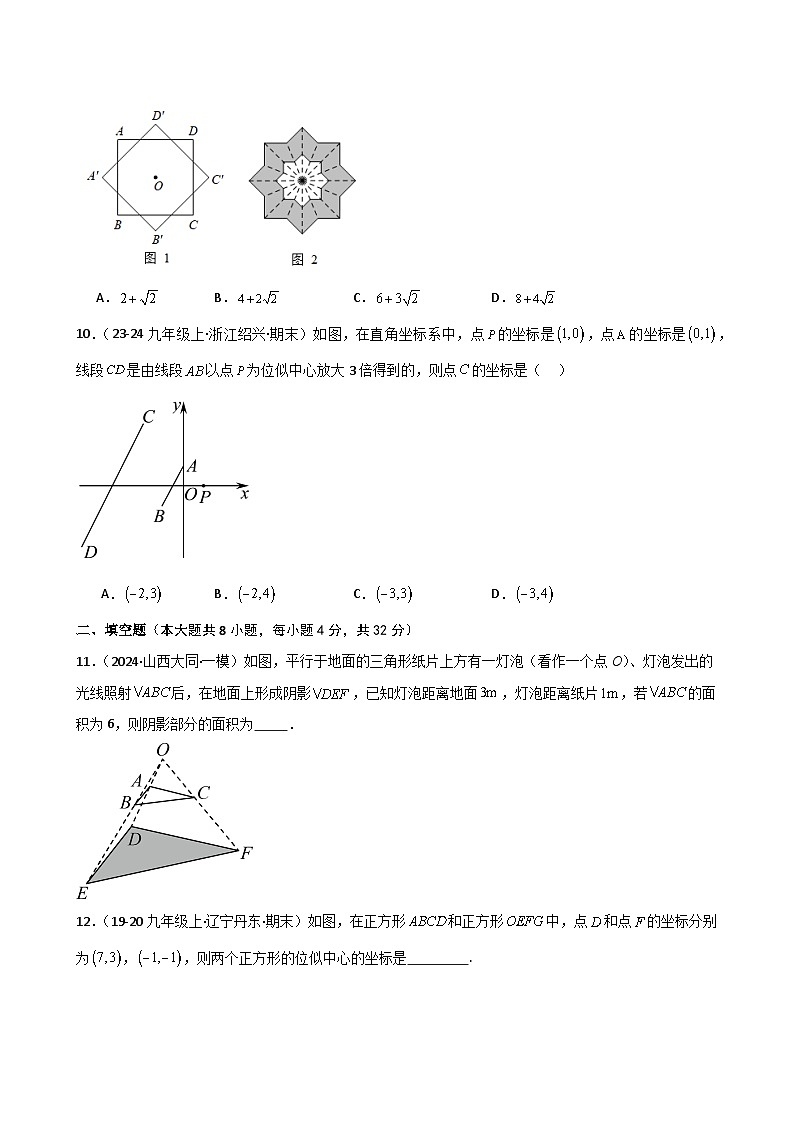
9．（22-23九年级上·浙江温州·阶段练习）如图1，正方形绕中心O逆时针旋转45°得到正方形，现将整个图形的外围以O为位似中心得到位似图形如图2所示，位似比为，若整个图形的外围周长为16，则图中的阴影部分面积为（ ）
A．B．C．D．
10．（23-24九年级上·浙江绍兴·期末）如图，在直角坐标系中，点的坐标是，点的坐标是，线段是由线段以点为位似中心放大3倍得到的，则点的坐标是（ ）
A．B．C．D．
二、填空题（本大题共8小题，每小题4分，共32分）
11．（2024·山西大同·一模）如图，平行于地面的三角形纸片上方有一灯泡（看作一个点O）、灯泡发出的光线照射后，在地面上形成阴影，已知灯泡距离地面，灯泡距离纸片，若的面积为6，则阴影部分的面积为 ．
12．（19-20九年级上·辽宁丹东·期末）如图，在正方形和正方形中，点和点的坐标分别为，，则两个正方形的位似中心的坐标是 .
13．（2024·广东广州·二模）如图，与是位似图形，点O为位似中心，．若的周长为4，则的周长为 ．
14．（2024·四川成都·二模）如图，和是以点O为位似中心的位似图形．若和的周长之比为，则 ．
15．（2020·湖南郴州·中考真题）在平面直角坐标系中，将以点为位似中心，为位似比作位似变换，得到．已知，则点的坐标是 ．

16．（23-24八年级下·江苏淮安·阶段练习）如图，在平面直角坐标系中，和是以原点O为位似中心的位似图形．若，的周长为3，则的周长为 ．

17．（2024·江苏盐城·三模）如图，以点为位似中心，将按相似比放大，得到，则点的对应点的坐标为 ．
18．（2023·陕西西安·模拟预测）如图，在平面直角坐标系中，正方形，，关于原点O位似，其中点B，，，都在x轴上，点在上，在上．依此方式，继续作正方形，若点坐标为，则点的坐标为 ．

三、解答题（本大题共6小题，共58分）
19．（8分）19．（23-24八年级下·山东济宁·期末）如图所示的平面直角坐标系中，的三个顶点坐标分别为，，，与关于坐标原点位似，且相似比为．
(1)在轴下方，画出：
(2)直接写出________．
(3)直接写出的面积________．
20．（8分）（23-24八年级下·山东威海·期末）已知， 在平面直角坐标系的位置如图所示，点A，B，C的坐标分别为， ，． 与 是以点 P 为位似中心的位似图形．
(1)请写出点P的坐标是 ．
(2)以点O为位似中心，在y轴左侧画出 的位似图形，使相似比为；
(3)若点为 内一点，则点M在内的对应点的坐标为 ．
21．（10分）（23-24八年级下·山东青岛·期末）已知，在平面直角坐标系的位置如图所示，点，，的坐标分别为，，．与是以点为位似中心的位似图形．
(1)写出点的坐标__________；
(2)以点为位似中心，在轴左侧画出的位似图形，使相似比为2∶1．
22．（10分）（23-24九年级上·河南新乡·期末）如图，在平面直角坐标系中，每个小正方形的边长均为1个单位长度，的顶点均在小正方形的格点上，请完成下列问题：
(1)画出关于轴对称的图形，并写出点的坐标；
(2)以点为位似中心，为位似比，在网格中画出放大后的对应图形，；
(3)求（2）中的面积．
23．（10分）（19-20九年级上·河北唐山·期末）如图，BD，AC相交于点P，连接AB，BC，CD，DA，∠DAP＝∠CBP．
(1)求证：△ADP∽△BCP；
(2)直接回答△ADP与△BCP是不是位似图形；
(3)若AB＝8，CD＝4，DP＝3，求AP的长．
24．（12分）（2023·湖北武汉·模拟预测）如图在的正方形网格中，每个小正方形的顶点叫做格点，已知A，B，C都是格点．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．

(1)如图1，将以点C为位似中心缩小，使缩小前、后对应边长的比为，得到，画出；
(2)如图2，点D也是格点，连接，在上画出点E，使；
(3)如图3，在边上分别画出点F，G，H，使的周长最小．
参考答案：
1．C
【分析】本题考查的是位似变换，掌握两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形是解题的关键．根据位似图形的定义解答即可．
【详解】解：根据位似图图形的定义可知选项A、B、D中的两个图形都是位似图形，C中的两个图形不是位似图形，
故选：C．
2．D
【分析】本题考查确定位似中心，理解位似图形的概念是解题的关键．
根据位似图形的概念，连接对应点，交点即是位似中心．
【详解】连接，，交于点，
∴点是位似中心，
故答案为：D．
3．A
【分析】本题主要考查位似变换．解题的关键是掌握位似图形是相似图形的特殊形式，位似比等于相似比的特点．
位似图形就是特殊的相似图形，位似比等于相似比，利用相似三角形的性质即可求解．
【详解】解：与是位似图形，位似比为，
，
即，
．
故选：A
4．A
【分析】本题考查了位似变换的概念和性质、相似三角形的性质，掌握位似的两个图形必须是相似形、对应边平行是解题的关键．根据位似变换的概念得到，根据相似三角形的性质解答即可．
【详解】解：∵，
∴，
∵是以点为位似中心经过位似变换得到的，
∴，，
∴，
∴，
∴的周长与的周长比是为，
故选：．
5．A
【分析】本题主要考查了位似变换的概念和性质，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或．
根据在平面直角坐标系中位似变换的性质解答即可．
【详解】解：线段两个端点的坐标分别为，以原点O为位似中心，在第一象限内将线段缩小为原来的后得到线段，
则点B与点D是对应点，
则点D的坐标为，即．
故选：A．
6．C
【分析】本题考查位似图形的性质，位似图形肯定是相似图形，位似比等于相似比，相似图形的面积比等于相似比的平方，由此可解．
【详解】解：，
，
和的相似比为，
和的面积之比为，
故选C．
7．C
【分析】根据位似的性质，连接并延长，观察交点即可求解．
【详解】解：如图所示，连接并延长，

∴的位似图形是．
故选：C．
【点睛】本题考查了位似图形的性质，熟练掌握位似图形的性质是解题的关键．
8．C
【分析】根据位似图形的性质和位似中心为原点得出比例式，即可求解
【详解】关于原点位似的两个图形上，一组对应点的坐标分别为和，
故，
解得：；
故选：C
【点睛】本题考查了位似图形，掌握位似图形的性质是解答该题的关键
9．C
【分析】由正方形的性质及旋转性质可得，且为等腰直角三角形，可以推出，可以计算出图2中整个图形面积为，通过位似图形的性质可得图2中间空白部分面积为：，最后求出阴影部分的面积即可．
【详解】如图，
∵正方形绕中心O逆时针旋转45°得到正方形，整个图形的外围周长为16，
∴，且为等腰直角三角形，
∴，
∴图2中整个图形面积：
∵将整个图形的外围以O为位似中心得到位似图形如图2所示，位似比为，
∴图2中间空白部分面积为：
图2中阴影部分面积为：
故选：C
【点睛】该题主要考查了旋转变换的性质、正方形的性质、位似图形等几何知识点及其应用；应牢固掌握旋转变换的性质、正方形的性质等几何知识点，这是灵活运用、解题的基础和关键．
10．A
【分析】本题主要考查了求位似图形对应点坐标，根据位似图形的性质可得，据此可得，即点的坐标是．
【详解】解：∵线段是由线段以点为位似中心放大3倍得到的，
∴，
∴，
∴，
∴点的坐标是，
故选A．
11．
【分析】本题考查的是位似的定义、相似三角形的应用，掌握相似三角形的性质是解题的关键．由题意可得，根据相似三角形的性质即可得到答案．
【详解】解：如图，
由题意可知，和是以点O为位似中心的位似图形，
∴，
∵已知灯泡距离地面，灯泡距离纸片，
∴，
∵的面积为6，
∴，
即阴影部分的面积为，
故答案为：．
12．或
【分析】根据位似变换中对应点的坐标的变化规律，分两种情况：一种是当点E和C是对应顶点，G和A是对应顶点；另一种是A和E是对应顶点，C和G是对应顶点.
【详解】∵正方形和正方形中，点和点的坐标分别为，
∴
（1）当点E和C是对应顶点，G和A是对应顶点，位似中心就是EC与AG的交点.
设AG所在的直线的解析式为
解得
∴AG所在的直线的解析式为
当时，，所以EC与AG的交点为
（2）A和E是对应顶点，C和G是对应顶点.，则位似中心就是AE与CG的交点
设AE所在的直线的解析式为
解得
∴AE所在的直线的解析式为
设CG所在的直线的解析式为
解得
∴AG所在的直线的解析式为
联立解得
∴AE与CG的交点为
综上所述，两个正方形的位似中心的坐标是或
故答案为或
【点睛】本题主要考查位似图形，涉及了待定系数法求函数解析，求位似中心，正确分情况讨论是解题的关键.
13．8
【分析】本题考查的是位似图形的概念、相似三角形的性质，熟记相似三角形的周长比等于相似比是解题的关键．
根据位似图形的概念得到，，进而得到，则，根据相似三角形的性质即可解答．
【详解】解：∵与是位似图形，
∴，，
∴，
∵，
∴的周长：的周长，
∵的周长为4，
∴的周长为8，
故答案为：8．
14．
【分析】本题考查的是位似变换、相似三角形的性质．根据位似图形的概念得到，，得到，根据相似三角形的性质得到，根据相似三角形的周长比等于相似比求出，即可求解．
【详解】解：∵和是以点O为位似中心的位似图形，
∴，，
∴，
∴，
∵和的周长之比为，
∴，
∴，
故答案为：．
15．．
【分析】直接利用位似图形的性质进而得出对应点坐标即可．
【详解】解：∵将△AOB以点O为位似中心，为位似比作位似变换，得到△A1OB1，A（2，3），
∴点A1的坐标是：，
即A1．
故答案为：．
【点睛】此题主要考查了位似变换，正确掌握位似图形的性质是解题关键．
16．6
【分析】本题考查坐标与位似．根据位似比等于相似比，周长比等于相似比，即可得出结果．
【详解】解：∵和是以原点O为位似中心的位似图形，，
∴和的相似比为：，
∴和的周长比为：，
∵的周长为3，
∴的周长为6；
故答案为：6．
17．或/或
【分析】本题主要考查了位似变换、相似三角形的判定与性质等知识，理解位似图形的定义和性质是解题关键．分与在轴同侧和与在轴异侧两种情况讨论，分别求解即可．
【详解】解：分两种情况讨论，
①如下图，当与在轴同侧时，过点作轴于点，过点作轴于点，
∵，，
∴，，，
∵将按相似比放大，得到，
∴，
∵，，
∴，
∴，即，
解得，，
∴，
∴；
②如下图，当与在轴异侧时，过点作轴于点，过点作轴于点，
由①可知，，，，
∵，，
∴，
∴，即，
解得，，
∴
∴．
故答案为：或．
18．
【分析】根据题意求出直线的解析式为，点均在直线上，再根据正方形的性质求出点，，，，的坐标即可．
【详解】解：∵点坐标为，四边形是正方形，
，
∵正方形，，关于原点O位似，
直线的解析式为，点均在直线上，
时，则，正方形的边长为2，
，
同理可得：，，
,故答案为：．
【点睛】本题考查的是位似变换、正方形的性质、图形的变化规律，掌握位似变换的概念和性质是解题的关键．
19．(1)画图见解析
(2)2
(3)
【分析】本题考查的是画位似图形，位似图形的性质，确定关键点的位似对应点是解题的关键．
（1）分别确定关于的位似对应点，再顺次连接即可；
（2）由位似图形的性质可得答案．
（3）利用割补法求解三角形的面积即可；
【详解】（1）解：如图，即为所求；
．
（2）解：由位似图形的性质可得：；
（3）解：．
20．(1)
(2)见解析
(3)
【分析】本题考查位似变换，（1）利用位似图形的性质得到位似中心的位置即可求解；
（2）根据点O为位似中心，相似比为作图即可；
（3）利用位似图形的性质求解即可．
【详解】（1）解：如图，连接、、，并延长相交于点P，
∴，
故答案为：；
（2）解：如图，即为所求；
（3）解：由题意得，点M在内的对应点的坐标为，
故答案为：．
21．(1)
(2)作图见解析
【分析】本题考查位似作图，涉及图形与坐标、找位似中心、作位似图形等知识，熟记位似性质是解决问题的关键．
（1）连接对应点并延长，交点就是，在平面直角坐标系中直接写出坐标即可得到答案；
（2）连接点与的三个顶点并延长，使，连接三个顶点即可得到．
【详解】（1）解：如图所示：
点的坐标；
（2）解：如图所示：
即为所求．
22．(1)，图见解析；
(2)图见解析；
(3)30.
【分析】本题考查的是作简单平面图形轴对称后的图形及作位似图形．掌握轴对称和位似图形的性质，是解题的关键
（1）根据轴对称的性质，画出即可；
（2）根据位似图形的性质，画出即可；
（3）用割补法求出面积即可．
【详解】（1）解：如图所示，即为所求作三角形，
点的坐标为；
（2）如图所示，即为所求作三角形，
（3）由题图，知，
与的位似比为，
面积比为．
．
23．(1)见解析；
(2)不是位似图形；
(3)6
【分析】（1）根据两角对应相等的两个三角形相似证明；
（2）根据位似图形的定义判断，即可；
（3）根据△ADP∽△BCP，得到，再证明△APB∽△DPC，根据相似三角形的性质列出比例式，代入计算得到答案．
【详解】（1）证明：∵∠DAP＝∠CBP，∠DPA＝∠CPB，
∴ △ADP∽△BCP．
（2）解：△ADP与△BCP不是位似图形．
理由是：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，那么这样的两个图形叫做位似图形，这个点叫做位似中心．△ADP与△BCP的对应点的连线交于一个点，
∴ △ADP与△BCP不是位似图形．
（3）解：∵△ADP∽△BCP，
∴，
∵∠APB＝∠DPC，
∴△APB∽△DPC，
∴，
∴，
解得AP＝6．
【点睛】本题考查的是位似变换的概念、相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．
24．(1)见解析
(2)见解析
(3)见解析
【分析】（1）延长分别交格点、格线于点，再连接，则即为所作；
（2）如图2，取格点M，连接交于E，根据边边边可证，可得，根据等腰三角形的性质和三角形的内角和定理可得，则点E即为所求；
（3）平移线段到，在上取格点F，取格点L，连接，交于点R，则是的垂直平分线，平移线段到，取格点，连接并延长交于点N，则是的垂直平分线，连接，分别交于点G，H，连接，则此时的周长最小．
【详解】（1）如图1， 即为所作；

（2）如图2，取格点M，连接交于E，则点E即为所求；

（3）如图3，平移线段到，在上取格点F，取格点L，连接，交于点R，则是的垂直平分线，平移线段到，取格点，连接并延长交于点N，则是的垂直平分线，连接，分别交于点G，H，连接，则此时的周长最小．点F，G，H即为所求．

【点睛】本题是网格作图题，主要考查了作位似图形、全等三角形的判定和性质、等腰三角形的判定和性质、平移的性质、线段垂直平分线的性质、轴对称的性质等知识，综合性较强，正确理解题意、熟练掌握相关图形的性质是解题的关键．