人教版（2024）九年级上册22.1.1 二次函数综合训练题

这是一份人教版（2024）九年级上册22.1.1 二次函数综合训练题，共39页。试卷主要包含了88，03，01等内容，欢迎下载使用。
本试卷满分120分，考试时间120分钟，试题共26题。答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置
选择题（10小题，每小题3分，共30分）
1．（2023春·湖南长沙·八年级校考期末）下列函数中，是二次函数的是（ ）
A．B．C．D．
2．（2023·黑龙江哈尔滨·哈尔滨市第六十九中学校校考模拟预测）将抛物线向左平移3个单位，再向下平移2个单位，得到的抛物线为（ ）
A．B．
C．D．
3．（2023·江苏淮安·统考三模）在某次试验中，测得两个变量x和y之间的4组对应数据如下表：
则x和y之间的关系最接近于下列各关系式中的（ ）
A．B．C．D．
4．（2023春·福建福州·八年级福建省福州延安中学校考期末）函数与在同一直角坐标系中的大致图象可能是（ ）
A． B． C． D．
5．（2023·山西大同·大同一中校考模拟预测）如图，有一个截面边缘为抛物线型的水泥门洞．门洞内的地面宽度为，两侧距地面高处各有一盏灯，两灯间的水平距离为，则这个门洞内部顶端离地面的距离为（ ）

A．B．8C．D．
6．（2023·统考三模）已知二次函数，当时，随的增大而增大，则（ ）
A．当时，的最大值为B．当时，的最大值为
C．当时，的最大值为D．当时，的最大值为
7．（2023·湖南怀化·统考三模）函数（，）的图象是由函数（，）的图象轴上方部分不变，下方部分沿轴向上翻折而成，如图所示，则下列结论正确的是（ ）
①；②；③；④将图象向上平移1个单位后与直线有3个交点．

A．①②B．①③④C．①②④D．①②③④
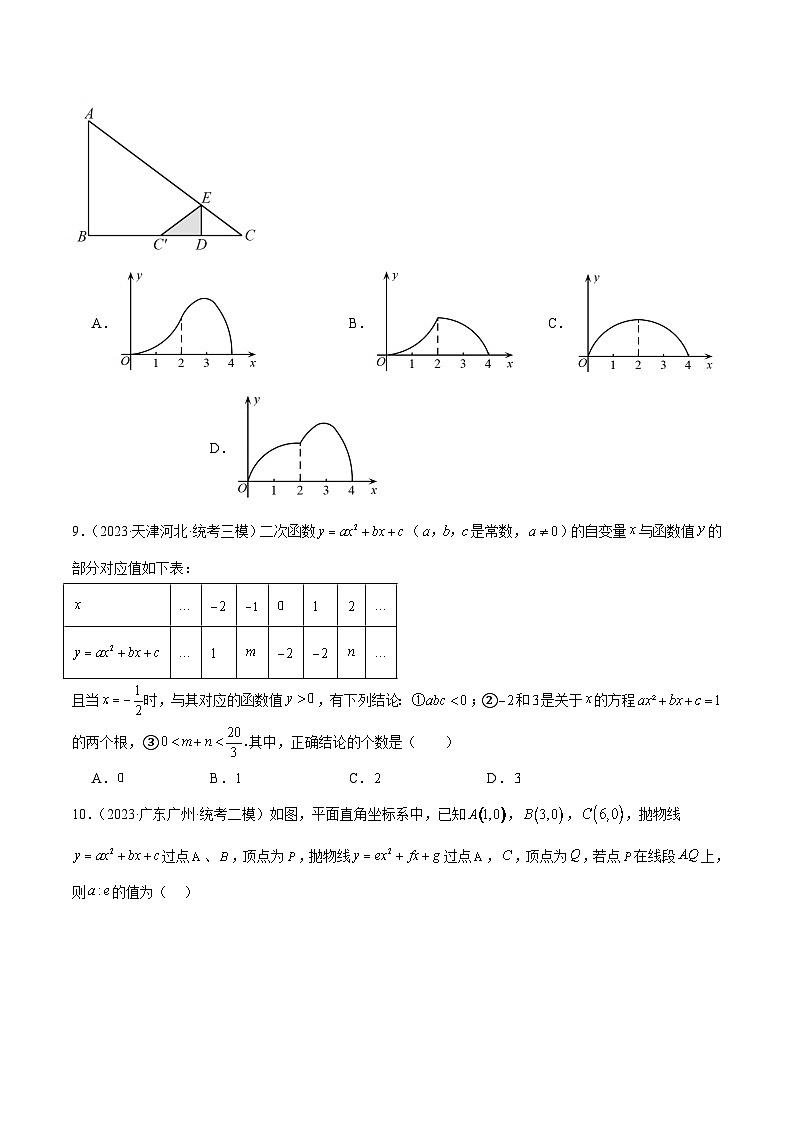
8．（2023·辽宁葫芦岛·统考二模）如图，在中，，，点从点出发沿方问以向点匀速运动，过点作于点．以所在直线为对称轴，将折叠，点的对应点为，移动过程中与重叠部分的面积为，运动时间为，则与之间函数关系的图象大致是（ ）

A． B． C． D．
9．（2023·天津河北·统考三模）二次函数（是常数，）的自变量与函数值的部分对应值如下表：
且当时，与其对应的函数值，有下列结论：；②和是关于的方程的两个根，③其中，正确结论的个数是（ ）
A．B．C．D．
10．（2023·广东广州·统考二模）如图，平面直角坐标系中，已知，，，抛物线过点、，顶点为，抛物线过点，，顶点为，若点在线段上，则的值为（ ）

A．B．C．D．
二、填空题（8小题，每小题3分，共24分）
11．（2023·浙江·九年级假期作业）请写出一个图像关于对称的二次函数的表达式 ．
12．（2023·福建福州·福建省福州第十九中学校考模拟预测）二次函数 的对称轴是直线 ．
13．（2023·全国·九年级假期作业）已知如图，平面直角坐标系中，一条直线与抛物线相交于、两点，求当时的x的取值范围是 ．

14．（2023春·浙江宁波·八年级校联考期中）对于竖直向上抛出的物体，在不考虑空气阻力的情况下，有如下的关系式：，其中h是物体上升的高度，v是抛出时的速度，g是重力加速度（），t是抛出后的时间．如果一物体以的初速度从地面竖直向上抛出，经过 秒钟后它在离地面高的地方．
15．（2023·浙江杭州·杭州市十三中教育集团（总校）校考三模）定义新运算：对于任意实数a，b，都有，例如1．若y关于x的函数的图象与x轴仅有一个公共点，则实数k的值为 ．
16．（2023·福建福州·福建省福州延安中学校考三模）如图，在正方形中，点，点，则二次函数与正方形有交点时，的最大值是 ．

17．（2023·吉林长春·统考二模）如图，抛物线与轴交于两点（点在的左边），与轴交于点，点为此抛物线上的一动点（点在第一象限），连接，则四边形面积的最大值为 ．

18．（2023·湖北武汉·统考模拟预测）函数（m为常数且）有下列结论：
①该函数图象与y轴交于点；
②若，当时，y随着x的增大而增大；
③该函数图象关于直线轴对称；
④若方程有三个实数根，则．
其中正确的结论是 ．（填写序号）
三、解答题（8小题，共66分）
19．（2023秋·山东济南·九年级统考期末）已知二次函数．
(1)将二次函数的解析式化为的形式．
(2)二次函数图像的对称轴是直线______、顶点坐标是______．
20．（2023·浙江·九年级假期作业）已知二次函数部分自变量与函数值的对应值如下表所示：
(1)求二次函数解析式；
(2)在平面直角坐标系中画出二次函数的图象；
(3)当时，的取值范围是____________．
21．（2023春·江苏盐城·八年级校考期中）已知抛物线（为常数），求证：无论为何值，抛物线与轴总有两个公共点．
22．（2023·河南周口·统考三模）科技进步促进了运动水平的提高．某运动员练习定点站立投篮，他利用激光跟踪测高仪测量篮球运动中的高度．图1所示抛物线的一部分是某次投篮训练中篮球飞行的部分轨迹，建立如图2所示的平面直角坐标系．已知篮球每一次投出时的出手点到地面的距离都为．当球运行至点处时，与出手点的水平距离为，达到最大高度为．

(1)求该抛物线的表达式．
(2)在球出手后，未达到最高点时，被防守队员拦截下来称为盖帽，但球到达最高点后，处于下落过程时，防守队员再出手拦截，属于犯规．在（1）的条件下，防守队员前来盖帽，已知防守队员的最大摸球高度为3.05m，则他应在运动员前面什么范围内跳起拦截才能盖帽成功？
23．（2023·全国·九年级假期作业）如图，已知抛物线的对称轴为直线，且与y轴的交点坐标为，直线l与x轴相交于点C．

(1)求该抛物线的表达式；
(2)如图，点P是该抛物线对称轴右侧图象上一动点，过点P作轴，，垂足分别为A，B．设点P的横坐标为m．当四边形为正方形时，求m的值．
24．（2023·湖北宜昌·统考二模）迅达水果合作社，为了提高樱桃和枇杷两种水果的销售量，决定将两种水果组合成礼盒销售．樱桃的收购单价是枇杷收购单价的倍，每个礼盒装有樱桃和枇杷，每盒还需其他成本元．
迅达水果合作社推出这礼盒后，经市场调查发现，该礼盒的日销售量（个）与礼盒的销售单价（元）之间满足一次函数．关于销售单价、日销售量、日销售利润的几组对应值如下表：
【提示：成本＝水果收购价＋其他成本；日销售利润＝（销售单价－成本）×日销售量】
(1)求与之间的函数关系式（不要求写的取值范围）；
(2)求樱桃的收购单价；
(3)进入月份，樱桃的收购单价上涨百分数为，枇杷的收购单价下降百分数也为，在销售过程中，日销售量与销售单价仍存在（1）中的关系，统计发现，当销售单价定为元时，日销售利润最大，求日销售最大利润．
25．（2023秋·广东惠州·九年级校考阶段练习）如图，抛物线 ，经过点 ，， 三点．

(1)求抛物线的解析式及顶点M的坐标；
(2)连接，，N为抛物线上的点且在第一象限，当时，求N点的坐标；
(3)在（2）问的条件下，过点C作直线轴，动点在直线l上，动点 在x轴上，连接 ，，，当m为何值时，的和最小，并求出 和的最小值．
26．（2023春·广东梅州·九年级统考期中）如图，抛物线与轴分别相交于，两点（点在点的左侧），是的中点，平行四边形的顶点，均在抛物线上．

(1)直接写出点的坐标；
(2)如图（1），若点的横坐标是，点在第二象限，平行四边形的面积是13，
①求直线的解析式；
②求点的坐标；
(3)如图（2），若点在抛物线上，连接，求证：直线过一定点．
第二十二章 二次函数 重难点检测卷
注意事项：
本试卷满分120分，考试时间120分钟，试题共26题。答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置
选择题（10小题，每小题3分，共30分）
1．（2023春·湖南长沙·八年级校考期末）下列函数中，是二次函数的是（ ）
A．B．C．D．
【答案】B
【分析】根据二次函数的概念逐项判断即可．
【详解】A．是一次函数，故此选项不符合题意；
B．是二次函数，故此选项符合题意；
C．不是二次函数，故此选项不符合题意；
D．是反比例函数，故此选项不符合题意，
故选：B．
【点睛】本题考查二次函数的概念，根据二次函数的定义“一般地，形如（a、b、c是常数，）的函数，叫做二次函数．其中x、y是变量，a、b、c是常量，a是二次项系数，b是一次项系数，c是常数项”．熟练掌握函数的概念及其表达式是解答的关键．
2．（2023·黑龙江哈尔滨·哈尔滨市第六十九中学校校考模拟预测）将抛物线向左平移3个单位，再向下平移2个单位，得到的抛物线为（ ）
A．B．
C．D．
【答案】B
【分析】根据函数图像的平移法则“左加右减、上加下减”直接求解即可得到答案．
【详解】解：将抛物线向左平移3个单位，再向下平移2个单位，得到的抛物线为，
故选：B．
【点睛】本题考查函数图像平移，熟记函数图像的平移法则“左加右减、上加下减”是解决问题的关键．
3．（2023·江苏淮安·统考三模）在某次试验中，测得两个变量x和y之间的4组对应数据如下表：
则x和y之间的关系最接近于下列各关系式中的（ ）
A．B．C．D．
【答案】B
【分析】当时，依次代入各个选项中，通过计算，比较即可得．
【详解】解：A、当时，；
B、当时，，接近；
C、当时，，
D、当时，；
综上可得，符合题意，
故选：B．
【点睛】本题考查了求函数值，解题的关键是掌握函数解析式的定义．
4．（2023春·福建福州·八年级福建省福州延安中学校考期末）函数与在同一直角坐标系中的大致图象可能是（ ）
A． B． C． D．
【答案】C
【分析】根据一次函数与二次函数的性质判断即可．
【详解】解：∵，
∴经过一、三象限；
当时，二次函数开口向上，与y轴的交点在负半轴上，
当时，二次函数开口向下，与y轴的交点在正半轴上，
∴只有选项C符合题意；
故选：C．
【点睛】题目主要考查一次函数与二次函数图象的判断，熟练掌握一次函数与二次函数的性质是解题关键．
5．（2023·山西大同·大同一中校考模拟预测）如图，有一个截面边缘为抛物线型的水泥门洞．门洞内的地面宽度为，两侧距地面高处各有一盏灯，两灯间的水平距离为，则这个门洞内部顶端离地面的距离为（ ）

A．B．8C．D．
【答案】D
【分析】建立直角坐标系，得到二次函数，门洞高度即为二次函数的顶点的纵坐标.
【详解】解：如图，以地面为x轴，门洞中点为O点，画出y轴，建立直角坐标系，

由题意可知各点坐标为，，，
设抛物线解析式为把B、D两点带入解析式，
∴，解得：，
∴解析式为，则，
所以这个门洞内部顶端离地面的距离为，
故选D.
【点睛】本题考查二次函数的简单应用，能够建立直角坐标系解出二次函数解析式是本题关键.
6．（2023·统考三模）已知二次函数，当时，随的增大而增大，则（ ）
A．当时，的最大值为B．当时，的最大值为
C．当时，的最大值为D．当时，的最大值为
【答案】B
【分析】根据题意，分当时，当时，根据二次函数的性质，得出的最值，进而即可求解．
【详解】解：当时，抛物线开口向上，对称轴为直线
∵当时，随的增大而增大，
∴
∴，
∴
∴，即的最大值为，故B选项正确，A选项错误；
当时，抛物线开口向下，对称轴为直线
∵当时，随的增大而增大，
∴，
∴
∴，
∴，即的最小值为，故C，D选项错误
故选：B．
【点睛】本题考查了二次函数的性质，分类讨论，熟练掌握二次函数的性质是解题的关键．
7．（2023·湖南怀化·统考三模）函数（，）的图象是由函数（，）的图象轴上方部分不变，下方部分沿轴向上翻折而成，如图所示，则下列结论正确的是（ ）
①；②；③；④将图象向上平移1个单位后与直线有3个交点．

A．①②B．①③④C．①②④D．①②③④
【答案】C
【分析】根据函数图象与x轴交点的横坐标求出对称轴为，进而可得，故①正确；由图象可得，当时，，可判段②；由函数图象与y轴的交点坐标为，的图象轴上方部分不变，下方部分沿轴向上翻折而成可知，故③错误；求出翻折前的二次函数解析式，然后根据平移的性质可得④正确．
【详解】解：由函数图象可得：与x轴交点的横坐标为－1和3，
∴对称轴为，即，
∴整理得：，故①正确；
由图象可得，当时，，故②正确；
∵与y轴的交点坐标为，
可知，开口向上，图中函数图象是由原函数下方部分沿轴向上翻折而成，
∴，故③错误；
设抛物线的解析式为，
代入得：，
解得：，
∴，
∴，
∴顶点坐标为，
∵点向上平移1个单位后的坐标为，
∴将图象向上平移1个单位后与直线有3个交点，故④正确；
故选：C．
【点睛】本题考查了二次函数的图象和性质，掌握二次函数的对称轴公式，顶点坐标的求法是解题的关键．
8．（2023·辽宁葫芦岛·统考二模）如图，在中，，，点从点出发沿方问以向点匀速运动，过点作于点．以所在直线为对称轴，将折叠，点的对应点为，移动过程中与重叠部分的面积为，运动时间为，则与之间函数关系的图象大致是（ ）

A． B． C． D．
【答案】A
【分析】分两种情况讨论：①当时，，可以求出抛物线解析式，从而得到函数图像；②当时，，可以求出抛物线解析式，从而得到函数图像．
【详解】解：∵，，
∴当点D在中点时，和B重合，
∵，，
∴，
∴，
∴，
∵点速度是，运动时间为，
∴，
∴，
①当时，
由题意可得：，
此时，S与之间函数关系的图像是顶点在原点，开口向上的抛物线；
②当时，如图所示，

此时，
∵，，
∴，，
∵，
同理可得：，
∴，
∴当时，S有最大值，最大值为2，
此时，S与之间函数关系的图象是开口向下的抛物线，且当时，S有最大值，
故选：A．
【点睛】本题考查动点问题的函数图像，关键是分段求出S与之间函数解析式．
9．（2023·天津河北·统考三模）二次函数（是常数，）的自变量与函数值的部分对应值如下表：
且当时，与其对应的函数值，有下列结论：；②和是关于的方程的两个根，③其中，正确结论的个数是（ ）
A．B．C．D．
【答案】B
【分析】①用待定系数法求出函数解析式，得出a、b、c的值，即可判定①；
②把，代入，看左右两边是否相等，可判定②；
③把，，，，代入，求出m、n值，可计算的值，即可判定③．
【详解】解：由表格可知：，，，，，，
分别代入，得
，解得：，
∴，
，
故错误；
把代入方程，
左边，右边，
∴左边=右边
把代入方程，
左边，右边，
∴左边=右边
和是关于的方程的两个根；
故正确；
把，，代入，得
，
把，，代入，得
，
故错误；
故选：B．
【点睛】本题考查二次函数的图象及性质；熟练掌握二次函数图象上点的特征，能够从表格中获取信息确定出对称轴是解题的关键．
10．（2023·广东广州·统考二模）如图，平面直角坐标系中，已知，，，抛物线过点、，顶点为，抛物线过点，，顶点为，若点在线段上，则的值为（ ）

A．B．C．D．
【答案】B
【分析】先分别求出抛物线的对称轴为直线，抛物线的对称轴为直线；然后把把抛物线的解析式设为交点式，从而求出点的坐标为，求出直线的解析式为，在求出在直线上，得到，即可求解得到答案
【详解】解：∵抛物线过点，
∴抛物线的对称轴为直线
∵抛物线过点，，
∴抛物线的对称轴为直线，
设抛物线的解析式为，
抛物线的解析式为，
当时，，
∴点的坐标为，
同理点的坐标为，
设直线的解析式为，
∴，
解得，
∴直线的解析式为，
∵点在线段上，
故，
即，
∴．
故选：B．
【点睛】本题考查了二次函数与一次函数综合，正确求出，的坐标是解题的关键．
二、填空题（8小题，每小题3分，共24分）
11．（2023·浙江·九年级假期作业）请写出一个图像关于对称的二次函数的表达式 ．
【答案】，答案不唯一
【分析】当只告诉一个对称轴时，可设二次项系数为简单数如1，得出表达式，然后把点的坐标代入即可．
【详解】∵图像是关于直线对称的二次函数，
∴可设这个二次函数解析式为：，
∴可取合适的点代入得，
∴这个二次函数解析式为：（答案不唯一．
故答案为：（答案不唯一．
【点睛】本题考查了待定系数法求二次函数的解析式，熟练掌握确定待定系数的方法是解决此题的关键．
12．（2023·福建福州·福建省福州第十九中学校考模拟预测）二次函数 的对称轴是直线 ．
【答案】
【分析】根据抛物线的解析式即可得到对称轴．
【详解】解：根据题意可得：
二次函数 的对称轴是直线：，
故答案为：．
【点睛】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在中，对称轴为，顶点坐标为．
13．（2023·全国·九年级假期作业）已知如图，平面直角坐标系中，一条直线与抛物线相交于、两点，求当时的x的取值范围是 ．

【答案】或
【分析】根据图象结合A，B两点的坐标求解即可．
【详解】解：由图象可得，
∵、
∴当或时，．
故答案为：或．
【点睛】本题考查了二次函数与一次函数的交点问题，利用数形结合的思想，熟练掌握数形结合思想是解本题的关键．
14．（2023春·浙江宁波·八年级校联考期中）对于竖直向上抛出的物体，在不考虑空气阻力的情况下，有如下的关系式：，其中h是物体上升的高度，v是抛出时的速度，g是重力加速度（），t是抛出后的时间．如果一物体以的初速度从地面竖直向上抛出，经过 秒钟后它在离地面高的地方．
【答案】1或4
【分析】把代入所给关系式求t的值即可．
【详解】解：由题意得：．
整理得，
解得．
∴1秒或4秒后，物体处在离抛出点高的地方．
故答案为：1或4．
【点睛】本题考查二次函数的应用；只需把相关数值代入所给关系式即可．
15．（2023·浙江杭州·杭州市十三中教育集团（总校）校考三模）定义新运算：对于任意实数a，b，都有，例如1．若y关于x的函数的图象与x轴仅有一个公共点，则实数k的值为 ．
【答案】或/0或
【分析】由定义的新运算求得y关于x的函数为：，再由y关于x函数的图象与x轴仅有一个公共点得到，求解即可．
【详解】解：∵，
∴
即，
∵的图象与x轴仅有一个公共点，令，得，
∴，
∴，
解得：或．
故答案为：或．
【点睛】本题主要考查了一元二次方程的根与二次函数图像和x轴交点坐标的关系，解题关键是熟记：一元二次方程有两个根，说明二次函数图像和x轴的横坐标有两个交点；一元二次方程有一个根，说明二次函数图像和x轴的横坐标有一个交点；一元二次方程（在实数范围）无解，说明二次函数图像和x轴的横坐标没有交点．
16．（2023·福建福州·福建省福州延安中学校考三模）如图，在正方形中，点，点，则二次函数与正方形有交点时，的最大值是 ．

【答案】
【分析】根据抛物线顶点坐标可确定其顶点在直线上移动，然后再确定当抛物线左侧经过点时，取得最大值，以此代入坐标求解即可．
【详解】解：由题意，该抛物线的顶点坐标为，
∴抛物线的顶点在直线上移动，
∵四边形为正方形，点，点，
∴点的坐标为，
如图所示，当抛物线左侧经过点时，取得最大值，

将代入得：，
解得：或（不合题意，舍去），
故答案为：．
【点睛】本题考查二次函数图象与性质，掌握抛物线顶点特征及运动轨迹，确定取得最值时的特殊位置是解题关键．
17．（2023·吉林长春·统考二模）如图，抛物线与轴交于两点（点在的左边），与轴交于点，点为此抛物线上的一动点（点在第一象限），连接，则四边形面积的最大值为 ．

【答案】
【分析】过作于，如图所示，根据抛物线图像与性质求出的坐标，再由，利用二次函数最值性质求出四边形面积最大值即可得到答案．
【详解】解：过作于，如图所示：

设，则，
抛物线与轴交于两点（点在的左边），与轴交于点，
当时，，即；当时，，解得或，即、，
，
，
抛物线开口向下，有最大值，即当时，四边形面积有最大值为，
故答案为：．
【点睛】本题考查二次函数综合的面积最值问题，熟练掌握二次函数综合面积问题解法，灵活运用二次函数图像与性质是解决问题的关键．
18．（2023·湖北武汉·统考模拟预测）函数（m为常数且）有下列结论：
①该函数图象与y轴交于点；
②若，当时，y随着x的增大而增大；
③该函数图象关于直线轴对称；
④若方程有三个实数根，则．
其中正确的结论是 ．（填写序号）
【答案】①③④
【分析】①将代入函数再化简绝对值即可判断；②求得时函数与轴的交点，再将代入函数验证即可；③将函数化为，根据对称轴的特征，设，求得和的函数值验证即可；④利用一元二次方程根的判别式分别讨论和时方程解的个数，再根据有三个实数根计算求值即可；
【详解】解：令代入函数可得，
∵，
∴，
∴该函数图象与y轴交于点，
故①正确；
若，则函数为，
可知当或时函数值为0，
当时，函数值为，此时的函数值大于的函数值，
∴当时，y不随x的增大而增大，
故②错误；
∵函数，
设，当时函数值为，
当时函数值为，
∴到直线的距离相等的两点的函数值相等，
∴该函数图象关于直线轴对称，
故③正确；
方程中，
当时可化为，
此时，
∵，
∴，即，方程有两个不等的实数根；
当时可化为，
此时，方程可以有两个不等根、两个相等根、无根；
若方程有三个实数根，则时方程有两个相等的根，
即，可得，
故④正确；
故答案为：①③④；
【点睛】本题考查了绝对值的化简，二次函数与坐标轴的交点，二次函数的图象性质，一元二次方程根的判别式等知识；掌握分类讨论的思想是解题关键．
三、解答题（8小题，共66分）
19．（2023秋·山东济南·九年级统考期末）已知二次函数．
(1)将二次函数的解析式化为的形式．
(2)二次函数图像的对称轴是直线______、顶点坐标是______．
【答案】(1)
(2)、
【分析】(1)根据配方法的基本步骤进行配方化简即可．
(2)根据抛物线顶点式的解析式特点计算即可．
【详解】（1）．
（2）∵，
∴对称轴为直线，顶点坐标为，
故答案为：、．
【点睛】本题考查了化抛物线的一般式为顶点式，确定对称轴，顶点坐标，熟练掌握配方法是解题的关键．
20．（2023·浙江·九年级假期作业）已知二次函数部分自变量与函数值的对应值如下表所示：
(1)求二次函数解析式；
(2)在平面直角坐标系中画出二次函数的图象；
(3)当时，的取值范围是____________．
【答案】(1)
(2)画图见详解
(3)
【分析】（1）用待定系数法即可求解；
（2）根据函数解析式，用描点法即可求解；
（3）根据自变量的取值范围，结合图示，即可确定函数值的取值范围．
【详解】（1）解：当时，；当时，；当时，，
∴，解方程得，
∴二次函数解析式为．
（2）解：二次函数解析式为，图像如图所示，
函数与轴的交点是，，与轴的交点是，对称轴为，符合题意．
（3）解：当时，根据（2）中图示可知，
当时，；当当时，；当时，．
∴当时，．
【点睛】本题主要考查待定系数法求二次函数解析式，根据函数解析式画函数图形，根据函数自变量求函数取值范围，掌握待定系数法解二次函数解析式，函数图像的性质是解题的关键．
21．（2023春·江苏盐城·八年级校考期中）已知抛物线（为常数），求证：无论为何值，抛物线与轴总有两个公共点．
【答案】见解析
【分析】求得判别式并分解得到平方与正数的和，得到判别式大于0即可证明．
【详解】证明：∵，
∴无论为何值，抛物线与轴总有两个公共点．
【点睛】本题主要考查了抛物线与x轴的交点问题，把抛物线与x轴的交点问题转化为一元二次方程的问题是解题的关键．
22．（2023·河南周口·统考三模）科技进步促进了运动水平的提高．某运动员练习定点站立投篮，他利用激光跟踪测高仪测量篮球运动中的高度．图1所示抛物线的一部分是某次投篮训练中篮球飞行的部分轨迹，建立如图2所示的平面直角坐标系．已知篮球每一次投出时的出手点到地面的距离都为．当球运行至点处时，与出手点的水平距离为，达到最大高度为．

(1)求该抛物线的表达式．
(2)在球出手后，未达到最高点时，被防守队员拦截下来称为盖帽，但球到达最高点后，处于下落过程时，防守队员再出手拦截，属于犯规．在（1）的条件下，防守队员前来盖帽，已知防守队员的最大摸球高度为3.05m，则他应在运动员前面什么范围内跳起拦截才能盖帽成功？
【答案】(1)
(2)应在运动员前面范围内跳起拦截才能盖帽
【分析】（1）根据题意得出，，设，待定系数法求解析式即可求解．
（2）根据题意，令，解方程即可求解．
【详解】（1）解：∵到地面的距离都为．当球运行至点处时，与出手点的水平距离为，达到最大高度为
∴，，
设抛物线解析式为，
将点代入得，，
解得：，
∴抛物线解析式为，
（2）将代入解析式，，
解得：或（舍去），
答：应在运动员前面范围内跳起拦截才能盖帽．
【点睛】本题考查了二次函数的应用，熟练掌握二次函数的性质是解题的关键．
23．（2023·全国·九年级假期作业）如图，已知抛物线的对称轴为直线，且与y轴的交点坐标为，直线l与x轴相交于点C．

(1)求该抛物线的表达式；
(2)如图，点P是该抛物线对称轴右侧图象上一动点，过点P作轴，，垂足分别为A，B．设点P的横坐标为m．当四边形为正方形时，求m的值．
【答案】(1)
(2)0或1
【分析】（1）利用待定系数法解答，即可；
（2）根据题意可得，再由正方形的性质可得，从而得到关于m的方程，即可求解．
【详解】（1）解：根据题意得：
，解得：，
∴抛物线的解析式为；
（2）解：∵直线与x轴相交于点C．
∴点，
∵轴，，垂足分别为A，B．点P的横坐标为m．
∴，
∴，，
∵四边形为正方形，
∴，
∴，
解得：（舍去）或或（舍去）或，
综上所述，m的值为0或1．
【点睛】本题主要考查了二次函数的的综合题，涉及了求二次函数的解析式，正方形的性质，利用数形结合思想解答是解题的关键．
24．（2023·湖北宜昌·统考二模）迅达水果合作社，为了提高樱桃和枇杷两种水果的销售量，决定将两种水果组合成礼盒销售．樱桃的收购单价是枇杷收购单价的倍，每个礼盒装有樱桃和枇杷，每盒还需其他成本元．
迅达水果合作社推出这礼盒后，经市场调查发现，该礼盒的日销售量（个）与礼盒的销售单价（元）之间满足一次函数．关于销售单价、日销售量、日销售利润的几组对应值如下表：
【提示：成本＝水果收购价＋其他成本；日销售利润＝（销售单价－成本）×日销售量】
(1)求与之间的函数关系式（不要求写的取值范围）；
(2)求樱桃的收购单价；
(3)进入月份，樱桃的收购单价上涨百分数为，枇杷的收购单价下降百分数也为，在销售过程中，日销售量与销售单价仍存在（1）中的关系，统计发现，当销售单价定为元时，日销售利润最大，求日销售最大利润．
【答案】(1)
(2)元/千克
(3)元
【分析】（1）根据题意和表格中的数据可以求得与之的函数解析式；
（2）根据题意可以列出方程，从而可以求得樱桃的收购单价；
（3）根据题意列出相应的关系式，利用二次函数的性质即可得出答案．
【详解】（1）解：设与之间的函数关系式为，过点和点，
∴，
解得：，
∴与之间的函数关系式为；
（2）设枇杷收购单价为元/千克，櫻桃的收购单价为元/千克，
依题意得：，
解得：，
∴（元/千克），
∴櫻桃的收购单价是元/千克；
（3）设销售单价定为元时，日销售利润最大，日销售利润为元，
此时日销售量，
∴
，
∵，
∴当时，可取得最大值，
解得：，
∴当，时，
（元），
∴日销售最大利润为元．
【点睛】本题考查待定系数法确定函数关系式，二次函数的应用、一元一次方程的应用．解题的关键是明确题意，找出所求问题需要的条件，利用函数和数形结合的思想解答．
25．（2023秋·广东惠州·九年级校考阶段练习）如图，抛物线 ，经过点 ，， 三点．

(1)求抛物线的解析式及顶点M的坐标；
(2)连接，，N为抛物线上的点且在第一象限，当时，求N点的坐标；
(3)在（2）问的条件下，过点C作直线轴，动点在直线l上，动点 在x轴上，连接 ，，，当m为何值时，的和最小，并求出 和的最小值．
【答案】(1)，抛物线的顶点M坐标为
(2)点N坐标为
(3)当时，的最小值为
【分析】（1）利用待定系数法求二次函数解析式即可；
（2）过点A作交抛物线于点N，则有，利用待定系数法分别求直线、的解析式，再联立方程组即可求解；
（3）将顶点向上平移3个单位得到点，连接交x轴于点，连接，则，证明四边形是平行四边形，可得，由图可知，当，，三点共线时，取最小值，利用待定系数法求直线的解析式，可得当 时，，从而求得，即，过点N作轴交延长线于点E，在中，利用勾股定理求得，，即可求解．
【详解】（1）解：∵抛物线 经过点 ，，，
∴，
解得：，
∴，
则抛物线的顶点M坐标为 ．
（2）解：设直线解析式，
将点， 代入，得：，
解得：，
则直线解析式为 ，
过点A作交抛物线于点N，则有，
则直线的解析式为，
将点 代入，得：，解得：，
∴直线解析式为，
由，解得：或 ，
∴点N坐标为．

（3）解：将顶点向上平移3个单位得到点，连接交x轴于点，连接、，则，
∵，，
∴轴，且，
∴，且，
∴四边形是平行四边形，
∴，
由作图知当，，三点共线时，取最小值，
设直线的解析式为，
将点，代入，得：，
解得：，
∴直线的解析式为，
当 时，，
∴，即，
此时过点N作轴交延长线于点E，
在中，
∵，，
∴，
∴，
∴当 时，的最小值为．

【点睛】本题考查用待定系数法求函数解析式、勾股定理、平行四边形的判定与性质、线段和最值、一次函数与二元一次方程组、一次函数与x轴的交点问题，熟练掌握相关知识，利用待定系数法求二次函数解析式是解题的关键．
26．（2023春·广东梅州·九年级统考期中）如图，抛物线与轴分别相交于，两点（点在点的左侧），是的中点，平行四边形的顶点，均在抛物线上．

(1)直接写出点的坐标；
(2)如图（1），若点的横坐标是，点在第二象限，平行四边形的面积是13，
①求直线的解析式；
②求点的坐标；
(3)如图（2），若点在抛物线上，连接，求证：直线过一定点．
【答案】(1)
(2)①；②
(3)见解析
【分析】（1）令，求出点，两点坐标，根据是的中点，即可求解；
（2）①先求出点，即可求得直线的解析式，
②过点作轴交直线于点，连接，设点，则点，可得，再由平行四边形的面积是13，可得，再根据，列出关于的方程，求出点的坐标，即可求解；
（3）设直线的解析式为，联立，可得，从而得到，再由平行四边形的性质，可得，，再由点在抛物线上，可得，从而得到直线的解析式为，即可求解．
【详解】（1）解：当时，则，
解得：，，
，，
是的中点，
；
（2）解：①点在抛物线上，
，
点，
设直线的解析式为，
把，代入得：，
解得，
直线的解析式为，
②如图（1），过点作轴交直线于点，连接，

设点，则点，
，
平行四边形的面积是13，
，
，
，
解得：或（舍去），
点，
点先向右平移3个单位，再向上平移2个单位到达点，
点先向右平移3个单位，再向上平移2个单位到达点；
（3）解：设直线的解析式为，
联立得：，
整理得：，
，
四边形为平行四边形，
，，
，
，
点在抛物线上，
，
解得：，
直线的解析式为，
直线过定点．

【点睛】本题主要考查了二次函数的综合题，平行四边形的性质，熟练掌握二次函数的图象和性质，利用数形结合思想解答是解题的关键．
x
1
2
3
4
y
0.01
2.88
8.03
15.01
…
…
…
…
销售单价（元/个）
日销售量有（个）
日销售利润（元）
x
1
2
3
4
y
0.01
2.88
8.03
15.01
…
…
…
…
销售单价（元/个）
日销售量有（个）
日销售利润（元）