第一次月考卷（南京专用）-2024-2025学年九年级数学上学期第一次月考模拟卷（江苏专用）

这是一份第一次月考卷（南京专用）-2024-2025学年九年级数学上学期第一次月考模拟卷（江苏专用），共26页。试卷主要包含了考试范围，方程的根为等内容，欢迎下载使用。
注意事项：
1．本试卷满分120分，考试时间120分钟，试题共27题。答题前，填写好自己的姓名、班级、考号等信息，请写在答题卡规定的位置上。
2．选择题必须使用2B铅笔填涂答案，非选择、判断题必须使用黑色墨迹签字笔或钢笔答题，请将答案填写在答题卡规定的位置上。
3．考试范围：九年级数学上册第1-2章（苏科版）
4．所有题目必须在答题卡上作答，在试卷上作答无效。考试结束后将试卷和答题卡一并交回。
一、选择题（6小题，每小题2分，共12分）
1．用配方法解方程x2-2x=0时，配方后所得的方程是（ ）
A．（x +1）2=1 B．（x -1）2=1 C．（x -1）2=-1 D．（x +1）2=-1
2．由著名导演张艺谋执导的电影《第二十条》因深刻体现了普法的根本是人们对公平正义的勇敢追求，创下良好口碑，自上映以来票房连创佳绩．据不完全统计，第一周票房约5亿元，以后两周以相同的增长率增长，三周后票房收入累计达约20亿元，设增长率为x，则方程可以列为（ ）
A．5+5x +5x2 =20 B．5（1+ x）2=20 C．5（1+ x）3=20 D．5+5（1+ x）+5（1+ x）2=20
3．圆的一条弦把圆分成度数的比为1:3的两条弧，则弦所对的圆周角等于（ ）
A．45°B．60°或120°C．135°D．45°或135°
4．如图，在中，，，，点在边上，，的半径长为，与相交，且点在外，那么的半径长可能是（ ）
A．B．C．D．
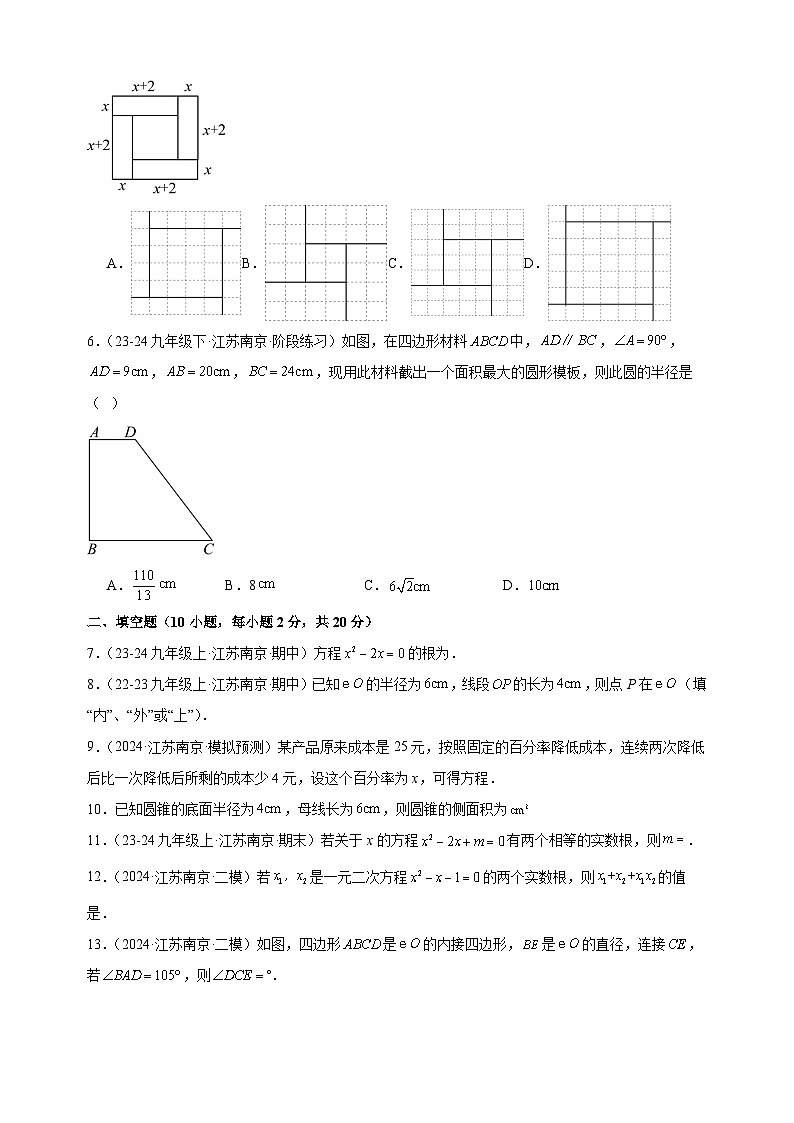
5．（22-23九年级上·江苏南京·阶段练习）我国古代数学家赵爽（公元世纪）在其所著的《勾股圆方图注》中记载过一元二次方程（正根）的几何解法，以方程即为例说明，记载的方法是：构造如图，大正方形的面积是．同时它又等于四个矩形的面积加上中间小正方形的面积，即，因此．则在下面四个构图中，能正确说明方程解法的构图是（ ）
A．B．C．D．
6．（23-24九年级下·江苏南京·阶段练习）如图，在四边形材料中，，，，，，现用此材料截出一个面积最大的圆形模板，则此圆的半径是（ ）
A．B．8C．D．
二、填空题（10小题，每小题2分，共20分）
7．（23-24九年级上·江苏南京·期中）方程的根为．
8．（22-23九年级上·江苏南京·期中）已知的半径为，线段的长为，则点P在（填“内”、“外”或“上”）．
9．（2024·江苏南京·模拟预测）某产品原来成本是25元，按照固定的百分率降低成本，连续两次降低后比一次降低后所剩的成本少4元，设这个百分率为x，可得方程．
10．已知圆锥的底面半径为，母线长为，则圆锥的侧面积为
11．（23-24九年级上·江苏南京·期末）若关于x的方程有两个相等的实数根，则．
12．（2024·江苏南京·二模）若是一元二次方程的两个实数根，则的值是．
13．（2024·江苏南京·二模）如图，四边形是的内接四边形，是的直径，连接，若，则°．

14．若，是一元二次方程的两个实数根，则的值为．
15．（2024·江苏南京·三模）如图，的直径是、是它的两条切线，与相切于点，并与、分别相交于、两点，设，则与的函数解析式为．
16．（2024·江苏南京·模拟预测）如图，点C是上一动点，B为一定点，D随着C点移动而移动，为的垂直平分线，，若半径为2，点B到点A的距离为4，则在C点运动过程中，的最大值为．
三、解答题（11小题，共88分）
17．（23-24九年级上·江苏南京·期末）解下列一元二次方程：
（1）；（2）．
18．（2024·江苏南京·模拟预测）南京有着“天下文枢”、“江南第一州”等美誉．美丽环境来之不易，为了美化环境，我市加大了对绿化的投资，年用于绿化投资万元，截止到年，这三年的绿化总投资为万元，求我市、这两年绿化投资的年平均增长率．
19．（23-24九年级上·江苏南京·期末）已知P是上一点，在上作两点，使得分别满足以下条件：
（1）在图①中，；
（2）在图②中，．
（说明：第（1）题只用无刻度的直尺作图，第（2）题只用圆规作图；保留作图痕迹，不写作法．）
20．（23-24九年级上·江苏南京·期中）如图，在中，，过点A，C的与，分别交于点D，E，连接．
（1）求证；
（2）延长，相交于点P，若，则的度数为°．
21．（23-24九年级上·江苏南京·阶段练习）如图，是的外接圆，E是的中点，AD是的高，连接

（1）求证：；
（2）若，，则______°．
22．（23-24九年级上·江苏南京·期中）已知关于x的一元二次方程（k为常数）．
（1）求证：无论k取何值，方程总有两个不相等的实数根；
（2）若该方程有两个实数根，，且，求k的值．
23．（23-24九年级上·江苏南京·期中）如图，菱形的对角线，BD交于点O，动点M从点A出发沿方向以的速度运动到点C，动点N从点B出发沿BD方向以的速度运动到点D．若点M，N同时出发，其中一个点停止运动时，另一个点也停止运动．

（1）出发1秒钟时，的面积=；
（2）出发几秒钟时，的面积为
24．（23-24九年级上·吉林四平·阶段练习）如图，为的直径，点是上方上异于的点，点是的中点，过点作交的延长线于点，连接，．
（1）求证：是的切线；
（2）若，，求图中阴影部分的面积．
25．（23-24九年级上·江苏南京·开学考试）如果关于的一元二次方程有两个实数根，且其中一个根是另一个根的3倍，那么称这样的方程为“三倍根方程”．例如，方程的两个根是1和3，则这个方程就是“三倍根方程”．
（1）下列方程是三倍根方程的是_______；
① ② ③
（2）若是关于的“三倍根方程”，求代数式的值．
26．（2024·江苏南京·二模）如图，铁匠师傅要在等边三角形铁皮（）上切一块最大的且无破损的圆形铁皮（）．
（1）如图①，三角形铁皮无破损，用直尺和圆规作出．（保留作图痕迹，不写作法）
（2）三角形铁皮上有一破损小洞（点P）．
①如图②，点P在的中心，用直尺和圆规作出．（保留作图痕迹，写出必要的文字说明）
②点P不在的中心．
i）点P的位置如图③所示，画出的示意图，并写出用直尺和圆规作的思路；
ii）随着点P位置的改变，的大小和位置都有可能发生变化．要使与i）中所画的圆的大小和位置都完全相同，那么点P可以在哪些位置？请描述出这些位置．
27．（23-24九年级上·江苏南京·阶段练习）【问题提出】
我们知道：同弧或等弧所对的圆周角都相等，且等于这条弧所对的圆心角的一半，那么，在一个圆内同一条弦所对的圆周角与圆心角之间又有什么关系呢？
【初步思考
（1）如图1，是的弦，，点、分别是优弧和劣弧上的点，则______， ；
（2）如图2，是的弦，圆心角，点是上不与、重合的一点，求弦所对的圆周角的度数为 ______；（用的代数式表示）
【问题解决】
（3）如图3，已知线段，点在所在直线的上方，且，用尺规作图的方法作出满足条件的点所组成的图形①直尺为无刻度直尺；②不写作法，保留作图痕迹）；
【实际应用】
（4）如图4，在边长为12的等边三角形中，点、D分别是边、上的动点，连接、，交于点，若始终保持，当点从点运动到点时，的最小值是______．
参考答案
一、选择题（6小题，每小题2分，共12分）
1．B
【分析】此题考查了配方法解一元二次方程，解答此题最重要的一步是在等式两边同时加上一次项系数一半的平方．把方程左边化为完全平方式即可．
【详解】解：x2-2x=0
两边加1得，x2-2x+1=0+1，即：（x -1）2=1．故选：B
2．D
【分析】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．根据第一周的票房及增长率，即可得出第二周票房约5（1+ x）亿元、第三周票房约5（1+ x）2亿元，根据三周后票房收入累计达约20亿元，即可得出关于x的一元二次方程，此题得解．
【详解】解：∵第一周票房约5亿元，且以后每周票房的增长率为x，
∴第二周票房约5（1+ x）亿元，第三周票房约5（1+ x）2亿元．
依题意得：5+5（1+ x）+5（1+ x）2=20．
故选：D
3．D
【分析】此题考查了圆周角定理，圆内接四边形的性质，
根据题意画出图形，然后利用圆周角定理，圆内接四边形的性质求解即可．
【详解】如图弦AB把圆分成度数的比为1:3的两条弧，
∴，，
∴，
故选：D．
4．B
【分析】本题考查了相交两圆的性质，点与圆的位置关系，勾股定理等知识点，能熟记相交两圆的性质和点与圆的位置关系的内容是解题的关键
连接交于，根据勾股定理求出的长，从而求出的长，再根据相交两圆的位置关系得出的范围即可．
【详解】解：连接交于，如图，

在中，由勾股定理得：，
则，
，
，
与相交，且点在外，必须，
即只有选项B符合题意，
故选：B．
5．D
【分析】本题主要考查一元二次方程的应用、完全平方公式的几何背景等知识点，通过图形直观得到面积之间的关系并用代数式表示出来是解答本题的关键．
根据题意，画出方程，即的拼图过程，由面积之间的关系即可解答．
【详解】解：方程，即的拼图如图所示：
中间小正方形的边长，其面积为25，
大正方形的面积：，其边长为7，
因此，D选项所表示的图形符合题意．
故选：D．
6．B
【分析】如图，由题意知，当与相切时，的面积最大，记切点分别为，连接，作于，证明四边形是矩形，则，，由勾股定理得，，由切线的性质，可得，四边形是正方形，设半径为，则，，由，即，计算求解，然后作答即可．
【详解】解：如图，由题意知，当与相切时，的面积最大，记切点分别为，连接，作于，
∵，，
∴，
又∵，
∴四边形是矩形，
∴，
∴，
由勾股定理得，，
由切线的性质，可得，四边形是正方形，
设半径为，则，，
∴，即，
解得，，
故选：B．
【点睛】本题考查了切线的性质，勾股定理，矩形的判定与性质，正方形的判定与性质等知识．熟练掌握切线的性质，勾股定理，矩形的判定与性质，正方形的判定与性质是解题的关键．
二、填空题（10小题，每小题2分，共20分）
7．，
【分析】本题主要考查了解一元二次方程，利用因式分解法解方程即可得到答案．
【详解】解：
或，
解得，．
故答案为：，．
8．内
【分析】题考查了点与圆的位置关系：设圆的半径为r，点到圆心的距离d，则有点P在圆外；点P在圆上；点P在圆内．
【详解】解：∵的半径为，线段的长为，
即点到圆心的距离小于圆的半径，
∴点P在内．
故答案为：内．
9．
【分析】本题主要考查了一元二次方程的应用，解题的关键是设降低的百分率为x，再表示出连续两次降低后的成本，一次降低后的成本，根据连续两次降低后比一次降低后所剩的成本少4元，列出方程即可．
【详解】解：设降低的百分率为x，根据题意得：
．
故答案为：．
10．
【分析】圆锥的侧面积（底面半径，母线长），把相应数值代入即可求解．
【详解】解：∵圆锥的底面半径为，母线长为，
∴圆锥的侧面积，
故答案为：．
【点睛】本题考查圆锥侧面积的求法，掌握相应公式是解题的关键．
11．1
【分析】根据判别式与根的关系得到，然后解关于m的方程即可．
【详解】解：根据题意得，，
解得．
故答案为1．
12．0
【分析】本题主要考查根与系数的关系，由根与系数的关系可得：，再把所求的式子进行整理，代入相应的值运算即可．
【详解】解：∵是一元二次方程的两个实数根，
∴，
∴．
故答案为：0．
13．15
【分析】本题主要考查了圆内接四边形的性质以及直径所对的圆周角等于，根据圆内接四边形的性质可得出，再根据直径所对的圆周角等于可得出，再利用角的和差关系可得出答案．
【详解】解：∵四边形是的内接四边形，且，
∴，
∵是的直径，
∴，
∴，
故答案为：15．
14．-2
【分析】利用根与系数的关系可得出x1+x2=-1、x1•x2=-3，将代数式x23-4x12+17进行转化后得出=-7-4（x12+x1）+17，再代入数据即可得出结论．
【详解】解：∵x1，x2是一元二次方程x2+x-3=0的两个实数根，
∴x1+x2=-1，x1•x2=-3，x22+x2=3，x12+x1=3，
∴x23-4x12+17=（3-x2）x2-4x12+17
=3x2-x22-4x12+17
=3x2-（3-x2）-4x12+17
=4x2-3-4x12+17
=4（-1-x1）-3-4x12+17
=-7-4（x12+x1）+17
=10-4×3
=-2
故答案为-2．
【点睛】本题考查了方程的解、根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，则x1+x2=-，x1x2=．
15．
【分析】根据切线长定理得到，，则，在中，根据勾股定理，就可以求出y与x的关系．
【详解】解：作交于F，
∵、与切于点定A、B，
∴，，
又∵，
∴，
∴四边形是矩形，
∴，，
∵，
∴，
∵切于E，
∴，，
则，
在中，
由勾股定理得：，
整理得：，
∴y与x的函数关系式是．
故答案为：．
【点睛】此题考查了切线的性质、切线长定理、矩形的判定与性质以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用．
16．
【分析】该题主要考查了勾股定理，正方形的性质和判定，垂直平分线的定义，圆中相关知识点，解题的关键是找到取得最大值时点C的位置．
过点作交所在直线于点，证明四边形是正方形，设，则，勾股定理得出，确定出时最大，求解即可；
【详解】解：过点作交所在直线于点，
∵为的垂直平分线，，
∴，
∵，
∴四边形是正方形，
设，则，
在中，，
故当最大时，最大，
∵，
∴时最大，即最大，
此时，
故答案为：．
三、解答题（11小题，共88分）
17．（1），；（2），．
【分析】本题考查了解一元二次方程因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
（1）利用因式分解法解方程即可；
（2）移项得到，然后利用因式分解法解方程．
【详解】（1）解：，
∴，
∴或，
∴，；
（2）解：，
∴，
∴，
∴，
∴或，
∴，．
18．
【分析】
本题考查一元二次方程的应用，理解题意，正确列出方程是解答的关键．
设这两年绿化投资的年平均增长率为，根据三年的绿化总投资钱数列方程求解即可．
【详解】解：设我市、这两年绿化投资的年平均增长率为，则年用于绿化投资万元，年用于绿化投资万元，
依题意得：，
整理得：，
解得：，（不合题意，舍去）．
答：我市、这两年绿化投资的年平均增长率为．
19．（1）见解析；（2）见解析
【分析】本题考查圆周角定理．掌握直径所对的圆周角是直角，同弧所对的圆周角是圆心角的一半，是解题的关键．
（1）过圆心，作一条直线，交圆上于，两点就是所求；
（2）在圆上选一点，以为圆心，的长为半径画弧，交于点，就是所求．
【详解】（1）解：如图，即为所求；
∵是直径，
∴；
（2）解：如图，即为所求．

证明：连接，如图所示：

以 A 为圆心， 的长为半径画弧，交 于点 B ，
连接 ，
则，
∴，
∴
20．（1）见解析；（2）38
【分析】此题考查了圆内接四边形的性质、等腰三角形的性质，熟记圆内接四边形的性质、等腰三角形的性质是解题的关键．
（1）根据圆内接四边形的性质得出，根据等腰三角形的性质得出，求出即可；
（2）根据对顶角相等及三角形内角和定理得出，结合等腰三角形性质及邻补角定义得出，则，根据三角形内角和定理求解即可．
【详解】（1），
，
又四边形为的内接四边形，
，
，
,
,
．
（2）如图，
，
，
，
，，，
，
，
，
故答案为：38．
21．（1）见解析；（2）
【分析】（1）连接，由垂径定理可知，结合AD是的高，可推出；再由即可求证；
（2）连接，利用求出即可进一步求出，再由可求，结合（1）中结论即可求解．
【详解】（1）证明：连接

∵E是的中点
∴
（2）解：连接，如图所示：

∵，
∵
∴
故答案为：
【点睛】本题考查了垂径定理、圆周角定理等相关知识点．熟记相关结论，作出正确的辅助线是解题关键．
22．（1）见解析；（2），
【分析】本题考查了一元二次方程根的判别式的意义，根与系数的关系，解一元二次方程；
（1）求出即可证明；
（2）根据根与系数的关系得出，，结合已知等式得出关于k的一元二次方程，解方程可得答案．
【详解】（1）证明：∵，
∴无论k取何值，方程总有两个不相等的实数根；
（2）解：∵方程有两个实数根，，
∴，，
又∵，
∴，
∴，
解得：，．
23．（1）15；（2）或或
【分析】本题考查了菱形的性质，一元二次方程与几何问题，掌握菱形的对角线互相垂直平分，根据题意进行分类讨论是解题的关键．
（1）根据菱形的性质得出，，再得出，最后根据三角形的面积公式求解即可；
（2）根据题意进行分类讨论即可①当时，点M在线段上，点N在线段上，②当时，点M在线段上，点N在线段上，③当时，点M在线段上，点N在线段上．
【详解】（1）解：∵四边形是菱形，
∴，，
当出发1秒钟时，，
∴，
∴的面积，
故答案为：15．
（2）解：∵
∴，
解得：，
当点M在线段上时，，即，
当点N在线段上时，，
设出发时间为t，则，
①当时，点M在线段上，点N在线段上，
，
∵的面积为
∴，
解得：（舍去），，
②当时，点M在线段上，点N在线段上，
，
∵的面积为
∴，
解得：，
③当时，点M在线段上，点N在线段上，
，
∵的面积为
∴，
解得：，（舍去），
综上：或或．
24．（1）见解析；（2）
【分析】本题主要考查了切线的判定、圆周角定理、勾股定理、三角形的面积公式、扇形的面积公式等．
（1）连接，由，得，而得到，由平行线的性质可得，从而即可得证；
（2）由圆周角定理可得，由勾股定理可得，从而得到，再由进行计算即可．
【详解】（1）证明：连接，
，点是的中点，
∴，
，
，
，
，
，
，
是的半径，且，
是的切线；
（2）解：为的直径，
，
，，
，
，
由（1）得，
，
图中阴影部分的面积是．
25．（1）③；（2）
【分析】本题主要考查解一元二次方程，“三倍根方程”，熟练掌握解一元二次方程是解题的关键．
（1）解一元二次方程然后根据“三倍根方程”的定义进行判定即可；
（2）设方程两个根为，，利用根与系数关系得：，，计算即可得到答案．
【详解】（1）解：对于①，解得，，不是“三倍根方程”；
对于②，解得，，不是“三倍根方程”；
对于③，解得，，是“三倍根方程”；
故答案为③
（2）解：设方程两个根为，，
利用根与系数关系得：，，
所以．
26．（1）见解析
（2）①见解析；②i）见解析；ii）见解析
【分析】本题考查了作三角形的内切圆，等边三角形，角平分线；
（1）作角平分线的交点，作三角形的内切圆；
（2）①方法一：使得为的三等分点；方法二：使得为的中心；方法三：作，的垂直平分线与的交点；
②i）如图⑤或图⑥，即为所求．思路1：作的角平分线，作分别与，相切，连接，交于点，过点P作，交于点O，思路2：作的角平分线，作点P关于的对称点，的延长线交于点M；作，在上截取，以为直径作，过点H作，交于点E；ii），分别是的角平分线，，分别交于点H，G，点P在上．
【详解】（1）解：如图①，⊙O即为所求，

（2）解：①方法一：使得为的三等分点；方法二：使得为的中心；方法三：作，的垂直平分线与的交点，作图如下：
②i）如图⑤或图⑥，即为所求．
思路1：作的角平分线，作分别与，相切，连接，交于点，过点P作，交于点O，以O为圆心，为半径作．
思路2：作的角平分线，作点P关于的对称点，的延长线交于点M；作，在上截取，以为直径作，过点H作，交于点E，可得；在上截取，可知；过点N作，交于点O，以O为圆心，为半径作．
ii）如图⑦，，分别是的角平分线，，分别交于点H，G，点P在上（点P不与G，H重合）．

27．（1）50，130；（2）；（3）见解析；（4）
【分析】（1）根据圆周角定理即可求出，根据圆内接四边形即可求出；
（2）分在优弧上和在劣弧上两种情况分类讨论即可求解；
（3）作线段的垂直平分线，以为直径作圆，交垂直平分线于点，以点为圆心，以为半径作圆，则（实线部分且不包含、两个端点）就是所满足条件的点所组成的图形；
（4）先证明，得到，，根据（3）问点P的运动轨迹是，，连接CO，证明，进而得到，，根据勾股定理求出，根据，可得，即可求出的最小值为．
【详解】解：（1），
．
故答案为：50，130；
（2）当在优弧上时，；
当在劣弧上时，；
故答案为：或
（3）如图（实线部分且不包含、两个端点）就是所满足条件的点所组成的图形．
证明：∵为的直径，
∴，
在中，∵点C在上，
由（2）得，
∴（实线部分且不包含、两个端点）就是所满足条件的点所组成的图形；
（4）解：如图，
∵为等边三角形，
∴，，
∵，
∴，
∴，
∵，
∴，
∴点P的运动轨迹是，
∴．
连接CO，
∵，
∴，
∴，，
∴，
在中，设，则，
根据勾股定理得，
解得，
∴，，
∵，
∴，
∴的最小值为．
故答案为：．
【点睛】本题考查了圆周角定理及其推论，圆内接四边形的性质，全等三角形的判定与性质，勾股定理，三角形三边关系等知识，综合性强，难度较大，解题时要熟知相关知识，注意在解决每一步时都要应用上一步结论进行解题．