初中数学北师大版（2024）八年级上册3 勾股定理的应用教学设计

这是一份初中数学北师大版（2024）八年级上册3 勾股定理的应用教学设计，共6页。教案主要包含了课堂引入，应用举例，拓展提升，达标检测，课堂总结，作业布置，知识网络，教学反思等内容，欢迎下载使用。
课题
3 勾股定理的应用
授课人
教
学
目
标
1.能灵活运用勾股定理及直角三角形的判别条件解决简单的实际问题.
2.在将实际问题抽象成数学问题的过程中,提高分析问题、解决问题的能力,渗透数学建模的思想.
3.培养学生应用数学的能力,体会数学在生活中的作用.
4.激发学生强烈的求知欲,使学生享受运用数学思想解决生活问题的成功体验.
教学
重点
应用勾股定理及直角三角形的判别条件解决简单的实际问题.
教学
难点
从实际问题中合理抽象出数学模型.
授课
类型
新授课
课时
教具
多媒体课件、三角尺
教学活动
教学
步骤
师生活动
设计意图
回顾
勾股定理及直角三角形的判别条件是什么?
学生回忆并回答,为本节课的学习提供迁移或类比方法.
活动
一:
创设
情境
导入
新课
【课堂引入】
观看图片,引出问题:有一块长方形绿地,绿地周边是小路,在绿地旁边的B处有健身器材.居住在A处的居民为了走近路而不惜践踏草地直接从A到B.
问题1:各位同学,你知道他们为什么不走绿地周边的小路吗?
问题2:如图1-3-10,假设入口A到拐角C处3米,拐角C到健身器材B处4米,你能计算出小草受伤的代价是他们少走几步吗?(假设2步为1米)
图1-3-10
用学生熟悉的生活实例引入并提出问题,使学生的参与兴趣浓厚、探究热情高涨,既复习了本节课需要用到的基本事实“两点之间,线段最短”和勾股定理的计算,又为下一环节奠定了良好的课堂氛围基础.
活动
二:
探究
与
应用
【探究1】
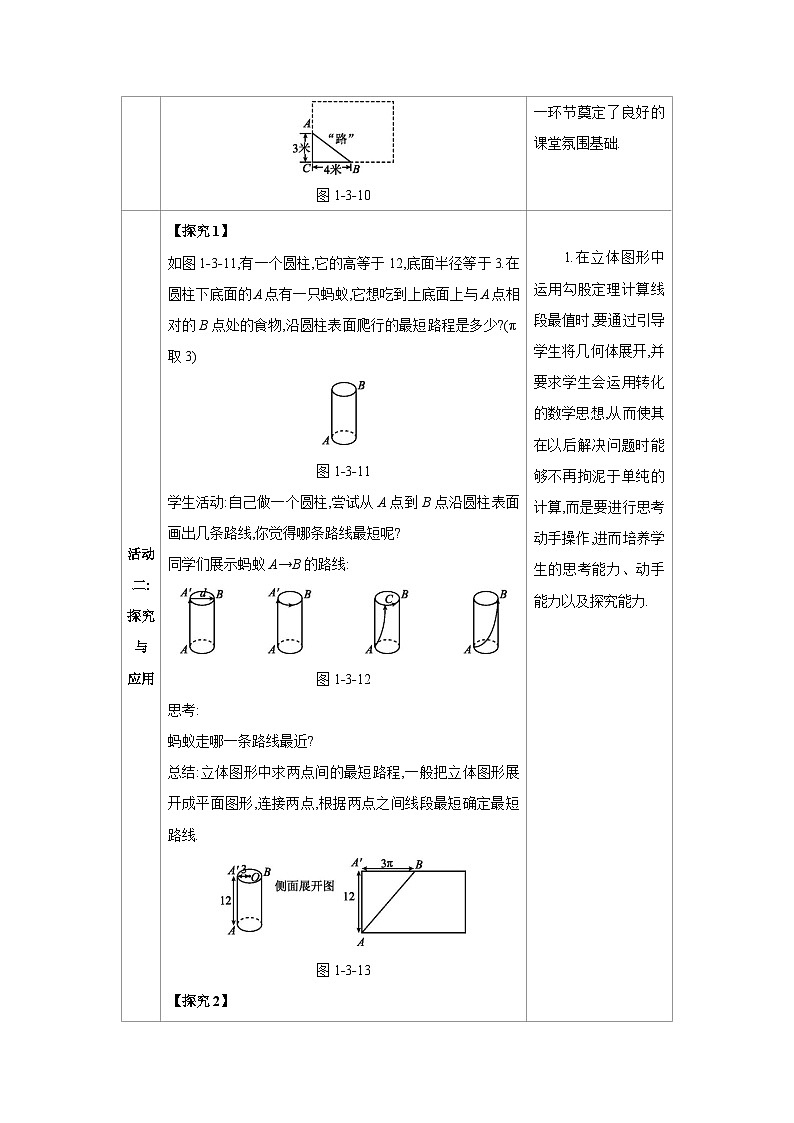
如图1-3-11,有一个圆柱,它的高等于12,底面半径等于3.在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱表面爬行的最短路程是多少?(π取3)
图1-3-11
学生活动:自己做一个圆柱,尝试从A点到B点沿圆柱表面画出几条路线,你觉得哪条路线最短呢?
同学们展示蚂蚁A→B的路线:
图1-3-12
思考:
蚂蚁走哪一条路线最近?
总结:立体图形中求两点间的最短路程,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
图1-3-13
【探究2】
李叔叔想要检测雕塑底座正面的边AD和边BC是否分别垂直于底边AB,但他只随身带了卷尺.
图1-3-14
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD的长是30 cm,边AB的长是40 cm,点B,D之间的距离是50 cm.边AD垂直于AB吗?
(3)小明随身只有一个长度为20 cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
方法总结:判断线段的垂直关系时,一般是把线段放到三角形中,利用勾股定理的逆定理证得直角三角形,进而得到线段的垂直关系.
1.在立体图形中运用勾股定理计算线段最值时,要通过引导学生将几何体展开,并要求学生会运用转化的数学思想,从而使其在以后解决问题时能够不再拘泥于单纯的计算,而是要进行思考动手操作,进而培养学生的思考能力、动手能力以及探究能力.
2.运用直角三角形的判别条件来解决实际问题,让学生学会分析问题,利用允许使用的工具灵活处理问题.
【应用举例】
例 (教材例题)图1-3-15是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3 m,CD=1 m,试求滑道AC的长.
图1-3-15
变式训练
吴老师在与同学们进行“蚂蚁怎样爬最近”的课题研究时设计了以下问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路程.
如图1-3-16,长方体的长为9 cm,宽为7 cm,高为12 cm,一只蚂蚁欲从长方体底面上的点A沿长方体表面爬到点C1处,怎样爬行,路线最短?
本例题是利用勾股定理解决实际问题的又一个类型,在训练学生的读题能力和规范书写解题过程的能力的基础上,可以使学生进一步理解勾股定理,体会数学与现实世界的联系.
活动
二:
探究
与
应用

图1-3-16 图1-3-17
按照图1-3-17②方式进行展开,在Rt△AC1B中运用勾股定理计算AC1的长度.
你能求出最短路程吗?
方法总结:在立体图形中运用勾股定理解决实际问题,一定要注意转化思想的运用,通常采取的方式是将立体图形进行展开,从而转化为平面图形,接着通过构造直角三角形,运用勾股定理进行问题求解.
【拓展提升】
1.甲、乙两位探险者到沙漠探险,某日早晨8:00,甲先出发,他以6 km/h的速度向正东匀速行走,1 h后乙出发,他以5 km/h的速度向正北匀速行走.上午10:00,甲、乙两人相距多远?
2.如图1-3-18,台阶A处的蚂蚁要到B处搬运食物,它怎么走最近?并求出最近距离(每级台阶完全相同).
图1-3-18
3.如图1-3-19,一个无盖的长方体盒子的长、宽、高分别为12 cm,8 cm,6 cm,一尺蚂蚁想从盒底的点A处沿盒的表面爬到盒顶的点B处,你能帮蚂蚁设计一条最短的路线吗?蚂蚁要爬行的最短路程是多少?
图1-3-19
审题是解题的关键,通过运用勾股定理,学会解决简单的实际问题,让学生认识到数学在现实世界中有着广泛的应用,培养了学生的应用意识.
活动
三:
课堂
总结
反思
【达标检测】
1.如图1-3-20,一只蚂蚁从一个正方体纸盒的点A沿纸盒表面爬到点B,它所爬过的最短路径(虚线)在侧面展开图中的位置是图1-3-21中的( )
图1-3-20
图1-3-21
学以致用,当堂检测,及时获知学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高,明确哪些学生需要在课后加强辅导,达到全面提高的目的.
活动
三:
课堂
总结
反思
2.如图1-3-22,一圆柱高8 cm,底面半径为2 cm,一只壁虎从上底面的点A爬到下底面与点A相对的点B处吃食,它爬行的最短路程(π取3)大约是( )
A.20 cm B.14 cm C.10 cm D.无法确定

图1-3-22 图1-3-23
3.小杨从学校出发向南走了150米,接着又向东走了360米到达了九龙山商场,则学校与九龙山商场的距离是
米.
4.如图1-3-23,阴影部分的半圆的面积是多少?(π取3.14)
【课堂总结】
学生活动:通过本堂课的学习,你有哪些收获?你有哪些困惑?对同学们,你有哪些温馨提示?
教学说明:学生畅谈自己的收获,通过本节课的学习,同学们经历了运用勾股定理解决简单实际问题的过程,体会转化思想及数学和生活的密切联系.
【作业布置】
课本P14习题1.4中的T3,T4.
【知识网络】
勾股定理
勾股定理的逆定理
作用
在抽象出的直角三角形中利用勾股定理求解
判断抽象出的三角形是不是直角三角形
关键
从实际问题中抽象出直角三角形
思想方法
方程思想
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
兴趣是最好的老师,学生只有对数学感兴趣,才想学、乐学,最后学会、学好,这就要求老师从“入趣点”着手.通过学生身边熟悉的问题引入,可以引起学生的情感共鸣,拉近与学生的距离,激发学生的学习兴趣.
②[讲授效果反思]
学生对知识的形成需要一个过程,甚至是反复的学习,本节课知识容量大,如果仅仅将解题过程投放在屏幕上,学生根本来不及思考,所以在教学中板书必不可少,它既能给学生的思维增添时间和空间,又可以规范学生解题的格式.
③[师生互动反思]


④[习题反思]
好题题号
错题题号
反思,更进一步提升.