吉林省长春外国语学校2024-2025学年高二上学期9月月考数学试题（Word版附解析）

这是一份吉林省长春外国语学校2024-2025学年高二上学期9月月考数学试题（Word版附解析），文件包含吉林省长春外国语学校2024-2025学年高二上学期9月月考数学试题Word版含解析docx、吉林省长春外国语学校2024-2025学年高二上学期9月月考数学试题Word版无答案docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。
出题人 ：康乐 审题人：李宁波
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页.考试结束后，将答题卡交回.
注意事项：
1.答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区.
2.选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚.
3.请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效.
4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑.
5.保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀.
第Ⅰ卷(选择题)
一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 若直线l的方向向量为，平面的法向量为，且，则实数x的值是（ ）
A. B. C. D.
2. 已知直线，若，则实数（ ）
A. 或B. C. 或D.
3. 在空间四点O，A，B，C中，若是空间的一个基底，则下列命题不正确的是（ ）
A. O，A，B，C四点不共线
B. O，A，B，C四点共面，但不共线
C. O，A，B，C四点不共面
D. O，A，B，C四点中任意三点不共线
4. 若直线5x＋4y＝2m＋1与直线2x＋3y＝m的交点在第四象限，则实数m的取值范围是（ ）
A. (－∞，2)B.
C. (－∞，－3)D.
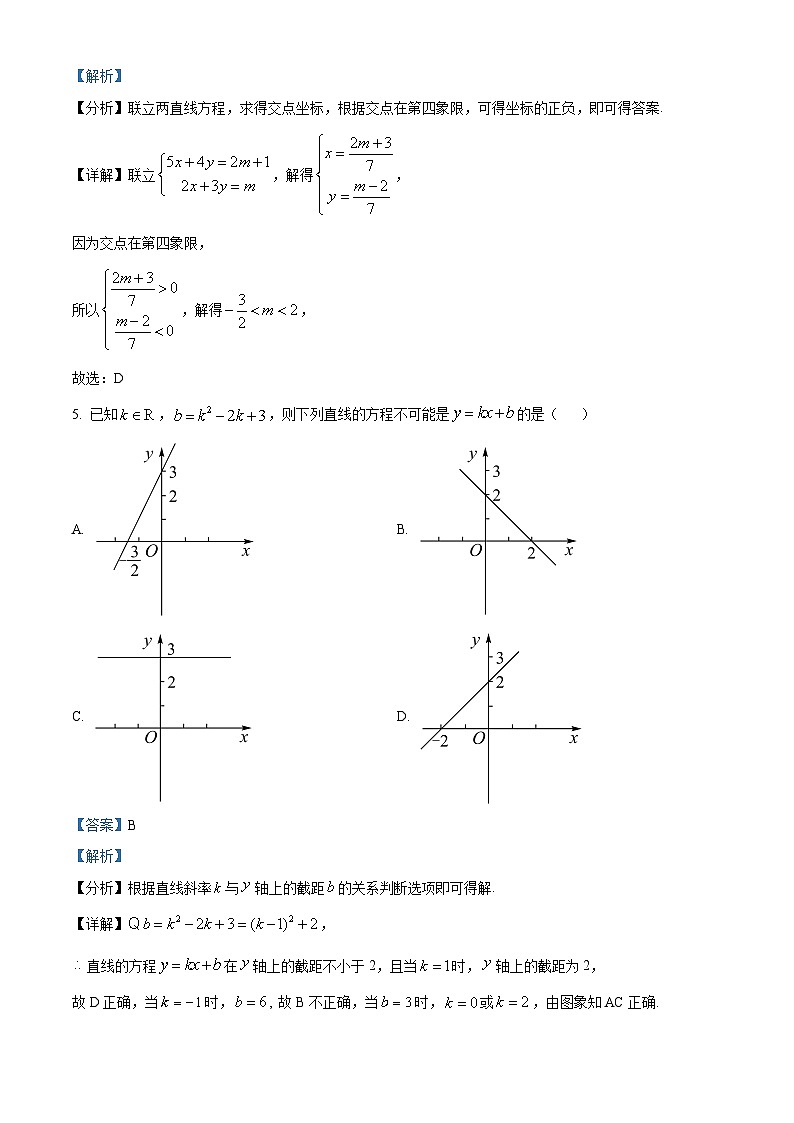
5. 已知，，则下列直线方程不可能是的是（ ）
A. B.
C D.
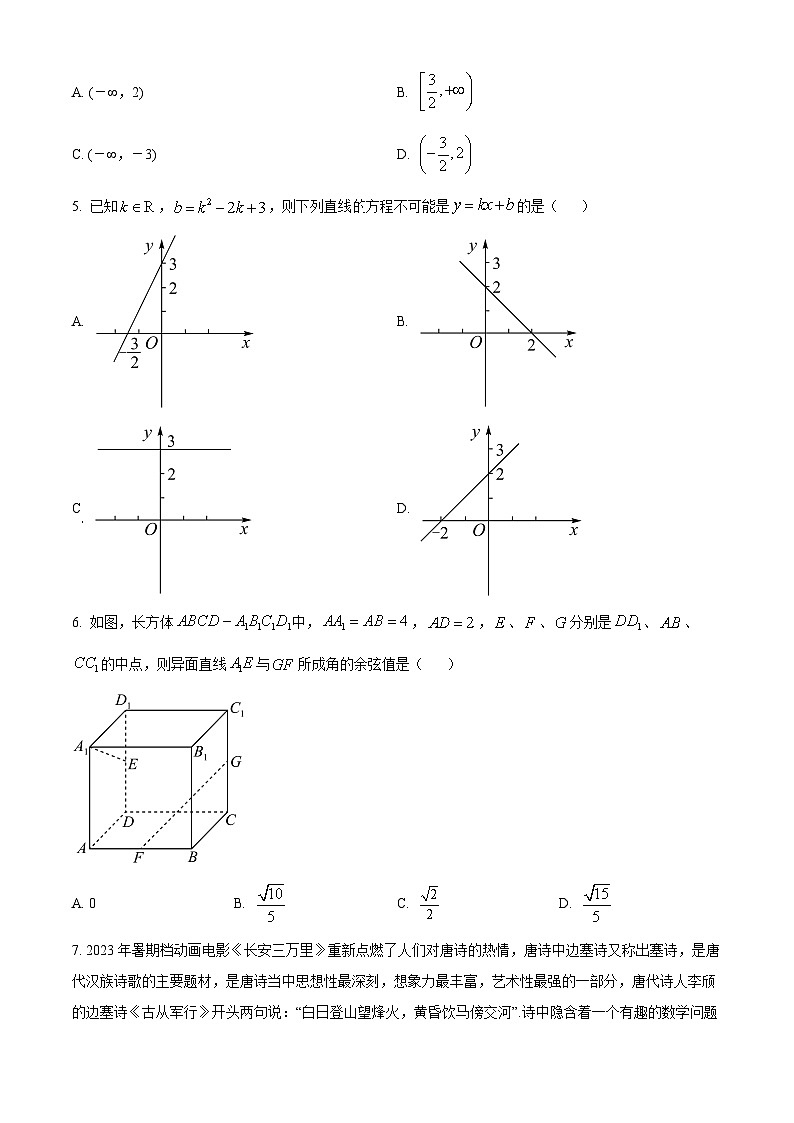
6. 如图，长方体中，，，、、分别是、、的中点，则异面直线与所成角的余弦值是（ ）
A. 0B. C. D.
7. 2023年暑期档动画电影《长安三万里》重新点燃了人们对唐诗的热情，唐诗中边塞诗又称出塞诗，是唐代汉族诗歌的主要题材，是唐诗当中思想性最深刻，想象力最丰富，艺术性最强的一部分，唐代诗人李颀的边塞诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河”.诗中隐含着一个有趣的数学问题——“将军饮马”，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回军营，怎样走才能使总路程最短？在平面直角坐标系中，设将军的出发点是，军营所在位置为，河岸线所在直线的方程为，若将军从出发点到河边饮马，再回到军营（“将军饮马”）的总路程最短，则（ ）
A. 将军从出发点到河边的路线所在直线的方程是
B. 将军在河边饮马地点的坐标为
C. 将军从河边回军营的路线所在直线的方程是
D. “将军饮马”走过的总路程为5
8. 如图，在正方体中，为棱上的一个动点，为棱上的一个动点，则平面与底面所成角的余弦值的取值范围是（ ）
A. B. C. D.
二、多项选择题：本题共3题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．
9. 直线过，两点，那么直线的倾斜角有可能是（ ）
A. B. C. D.
10. 如图，在平行六面体中，设，若为与的交点，则下列等式正确的是（ ）
A. B.
C. D.
11. 已知和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线，公垂线与两条直线相交的点所形成的线段，叫做这两条异面直线的公垂线段.两条异面直线的公垂线段的长度，叫做这两条异面直线的距离.如图，在棱长为1的正方体中，点在上，且；点在上，且.则下列结论正确的是（ ）
A. 线段是异面直线与的公垂线段
B. 异面直线与的距离为
C. 点到直线距离为
D. 点到平面的距离为
第Ⅱ卷（非选择题）
三、填空题：本题共3小题，每小题5分，共15分．
12. 已知点M(0，－1)，点N在直线x－y＋1＝0上，若直线MN垂直于直线x＋2y－3＝0，则N点的坐标是________．
13. 已知两条平行直线：，：，则与间的距离为______.
14. 在棱长为1的正方体中，，，分别在棱，，上，且满足，，，是平面，平面与平面的一个公共点，设，则 _________.
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15. 根据下列各条件分别写出直线的方程，并化成一般式.
（1）斜率是，且经过点；
（2）在轴和轴上的截距分别是和；
（3）经过点，且一个方向向量为.
16. 如图所示，在几何体中，四边形和均为边长为2的正方形，，底面，M、N分别为、的中点，.
（1）求证：平面；
（2）求直线与平面所成角的正弦值．
17. 已知直线方程．
（1）若直线的倾斜角为，求的值；
（2）若直线分别与轴、轴的负半轴交于、两点，为坐标原点，求面积的最小值及此时直线的方程．
18. 已知直线：，.
（1）证明直线过定点，并求出点的坐标；
（2）在（1）的条件下，若直线过点，且在轴上的截距是在轴上的截距的，求直线的方程；
（3）若直线不经过第四象限，求的取值范围.
19. 如图，在四棱锥中，底面是边长为6的正方形，是正三角形，平面，为的中点，，，分别是，，上的点，且满足．

（1）求平面与平面所成锐二面角的大小;
（2）在线段上是否存在点，使得直线与平面所成角为?若存在，求线段的长度；若不存在，请说明理由.