专题突破练习卷09 解三角形中三角形面积和周长（边）的最值（范围）问题-2025年高考数学一轮复习考点通关卷（新高考通用）

这是一份专题突破练习卷09 解三角形中三角形面积和周长（边）的最值（范围）问题-2025年高考数学一轮复习考点通关卷（新高考通用），文件包含专题突破卷09解三角形中三角形面积和周长边的最值范围问题原卷版docx、专题突破卷09解三角形中三角形面积和周长边的最值范围问题解析版docx等2份试卷配套教学资源，其中试卷共72页， 欢迎下载使用。

题型一：三角形面积的最值
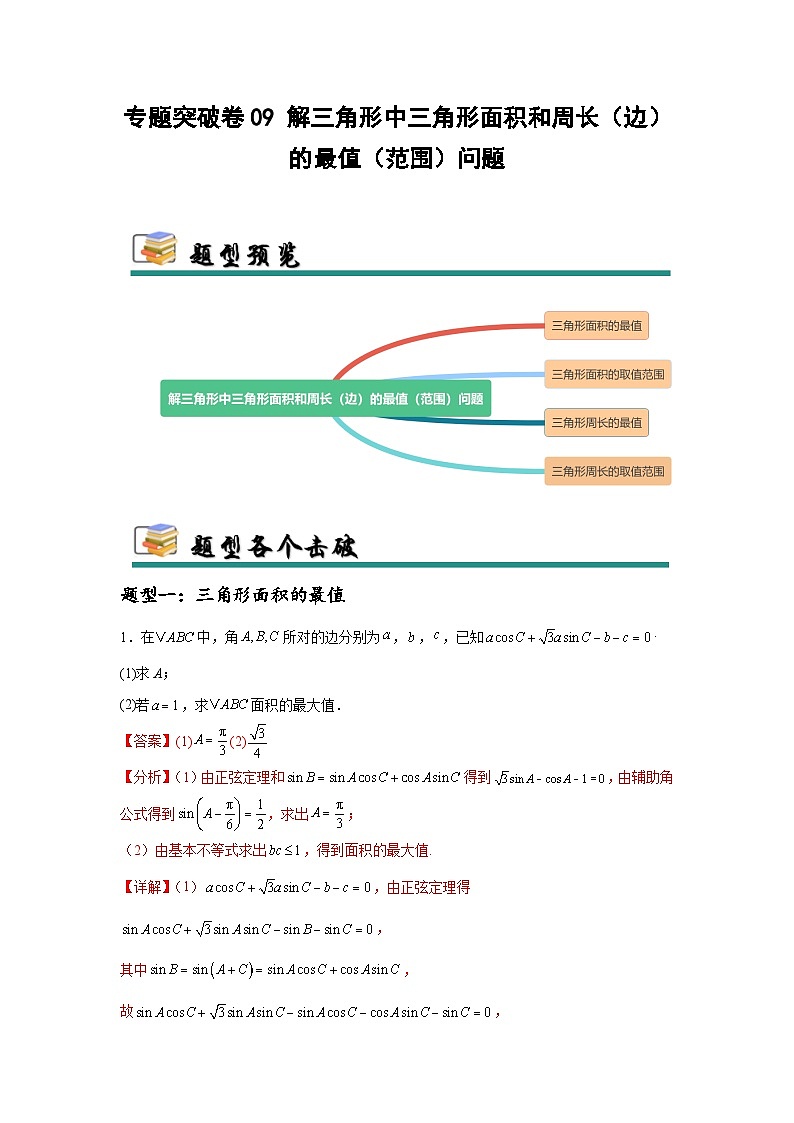
1．在中，角所对的边分别为，，，已知
(1)求A；
(2)若，求面积的最大值．
2．已知中，角A，B，C所对的边长分别为a，b，c；
(1)若满足，求证：．
(2)若在中，；
①BC边上的中线，求的面积的最大值．
②如图所示为等边三角形，，求当c为多少时，DE取得最大值．
3．在凸四边形中，已知
(1)若，求的值；
(2)求四边形面积的最大值.
4．已知函数的最大值是4，函数图象的一条对称轴是，一个对称中心是．
(1)求的解析式；
(2)已知中，是锐角，且，边长为3，求的面积的最大值．
5．在中，内角A，B，C所对的边分别为a，b，c，满足．
(1)求角B的大小；
(2)若的外接圆半径为1，求边长b的值；
(3)若，求的面积的最大值．
6．已知的内角A，，所对的边分别为，，，且最大，．
(1)求；
(2)若边上的高为4，求面积的最小值．
7．在中，分别是角的对边，．
(1)求角的大小及外接圆的半径的值；
(2)若是的内角平分线，当面积最大时，求的长．
8．在中，已知，，，为线段BC上一个动点．
(1)若AD为的角平分线，求线段AD的长；
(2)将折起到的位置，记二面角的大小为．
（i）若，且AD为的角平分线，求三棱锥外接球的面积；
（ii）若，求三棱锥外接球的面积最小值．
9．在中，角，，所对的边分别是，，，其面积记为，且满足
(1)求角；
(2)为边上一点，，且求的最小值.
(3)圆是外接圆，是圆外一点，，分别切圆于点，，若，求的最小值.
10．如图，在平面内，四边形满足，点在的两侧，，，为正三角形，设.

(1)当时，求；
(2)当变化时，求四边形面积的最大值.
题型二：三角形面积的取值范围
11．在①；②；③；这三个条件中任选一个，补充在下面的问题中，并解答问题（其中为的面积）．
问题：在中，角的对边分别为，满足：__________．
(1)求角的大小；
(2)若，角与角的内角平分线相交于点，求面积的取值范围．
12．请在①向量，，且；②这两个条件中任选一个，填入横线上并解答．
在中，内角，，的对边分别为，，，且满足_________．
(1)求角的大小；
(2)若为锐角三角形，，求面积的取值范围．
（注：如果选择条件①和条件②分别解答，按第一个解答计分）
13．已知三个内角，，的对边分别为，，，向量，，且.
(1)求角；
(2)若，求的面积的最大值；
(3)若，求的周长的取值范围.
14．已知的内角的对边分别为，且满足.
(1)求角的大小；
(2)若为锐角三角形且，求面积的取值范围.
15．已知中，角的对边分别为，.
(1)是边上的中线，，且，求的长度.
(2)若为锐角三角形，且，求面积的取值范围.
16．如图，某学校拟建一块五边形区域的“读书角”，三角形区域为书籍摆放区，沿着AB、AE处摆放折线形书架（书架宽度不计），四边形区域为阅读区，，m.
(1)求两区域边界的长度；
(2)区域为锐角三角形.
①若，求面积的最大值；
②若，求面积的取值范围.
17．已知，，分别为三个内角A，，的对边，．
(1)求证：；
(2)若为锐角三角形，且，求面积的取值范围．
18．从①；②这两个条件中任选一个，补充在下面的问题中，并解答．
在中，角A，B，C所对的边分别为a，b，c，且满足：______．注：如果选择多个条件分别作答，按第一个解答计分．
(1)求角C的大小；
(2)若为锐角三角形，且，求面积的取值范围；
(3)若，的内心为I，求周长的取值范围．
19．记锐角三角形的内角，，的对边分别为，，，已知，.
(1)求.
(2)求面积的取值范围.
20．的内角的对边分别为已知.
(1)若的周长等于3，求；
(2)若为锐角三角形，且；
①求；
②求面积的取值范围.
题型三： 三角形周长的最值
21．在中，内角所对的边分别为.
(1)求角；
(2)若的面积为，求周长的最小值.
22．如图，在中，．
(1)求的长；
(2)已知点D在平面内，且，求四边形的周长的最大值．
23．在①，②，③，这三个条件中任选一个，补充在下面的横线上，并加以解答.
已知的内角A，B，C所对的边分别是a，b，c，若__________.
(1)求角B；
(2)若，求周长的最小值.
24．已知中，角所对的边分别是，其中，．
(1)求的外接圆半径；
(2)求周长的最大值．
25．在中，为角对应的边，为的面积.且.
(1)求；
(2)若，求内切圆半径的最大值.
26．在中，角，，的对边分别为，，，且满足_______.从条件①、条件②这两个条件中任选一个补充在上面横线上作为已知，
(1)求角；
(2)若的面积为，为的中点，求的最小值.
条件①：；条件②：.
27．在锐角中，已知．
(1)求；
(2)求周长的最大值．
28．在中，内角的对边分别为，且.
(1)求角的大小；
(2)点是上的一点，，且，求周长的最小值.
29．定义函数的“源向量”为，非零向量的“伴随函数”为，其中为坐标原点.
(1)若向量的“伴随函数”为，求向量；
(2)在中，角的对边分别为，若函数的“源向量”为，且已知，；
（ⅰ）求周长的最大值；
（ⅱ）求的最大值.
30．在中，.
(1)求；
(2)若，求周长的最大值.
题型四：三角形周长的取值范围
31．在中，内角A，B，C的对边分别为a，b，c，且
(1)求C；
(2)若，求 周长的取值范围.
32．在中，角A，B，C所对的边分别为a，b，c，已知.
(1)求角B的大小；
(2)若，，求周长的取值范围.
33．在中，A，B，C所对的边分别为a，b，c，且．
(1)求B；
(2)若，求的周长l的取值范围．
34．在中，内角A，B，C的对边分别为a，b，c，且．
(1)求角B；
(2)若为锐角三角形，，D是线段AC的中点，求BD的长的取值范围．
35．锐角中角、、的对边分别为、、，且．
(1)求角的大小；
(2)若，求的取值范围．
36．在中，角，，所对的边分别记为，，，且．
(1)若，求的大小．
(2)若，求的取值范围．
37．已知的内角A、B、C所对的边长分别为a、b、c，且满足.请回答下列问题:
(1)证明:为等腰三角形;
(2)若的外接圆直径为1，试求周长的取值范围.
38．在中，内角，，所对的边分别为，，，满足．
(1)求内角的大小；
(2)角的平分线与边交于点，，若，求边的值；
(3)若，求的周长的取值范围．
39．已知分别为锐角三角形三个内角的对边，且.
(1)求;
(2)若，为的中点，求中线的取值范围.
40．如图，已知是边长为的正三角形，点在边上，且，点为线段上一点.
(1)若，求实数的值；
(2)求的最小值；
(3)求周长的取值范围.
1．在中，角A，B，C的对边分别为a，b，c，已知.
(1)求B；
(2)若外接圆的周长为，求周长的取值范围.
2．如图，在平面四边形中，

(1)若 与交于点，且，求的长；
(2)求四边形 周长的最大值．
3．如图，在中，，，，P为内一点，．

(1)若，求PA；
(2)（i）若，求．
（ii）求的取值范围．
4．在①；②，这两个条件中任选一个，补充在下面的横线上，并加以解答，在，角的对边分别是，边长，为的面积，若______（填条件序号）
(1)求角的大小；
(2)若为内一点且，求长度最大值；
(3)若为锐角三角形，求的内切圆半径的取值范围.
5．在中，内角，，的对边分别为，，，且．
(1)若，，成等差数列，求的面积；
(2)若，，成等比数列，求当取得最大值时，的周长．
6．已知、、分别为内角的对边，已知且．
(1)求角的大小；
(2)若的面积为，求的值；
(3)求周长的取值范围．
7．如图，在平面四边形中，，，，.
(1)证明：；
(2)求面积的最大值；
(3)设为线段的中点，求的最大值.
8．在锐角三角形中，内角的对边分别为，且．
(1)求角的大小；
(2)若，求面积的取值范围．
9．已知在，角所对的边分别是，且．
(1)求的大小；
(2)若，求面积的取值范围．
10．在中，内角，，的对边分别为，，，且满足.
(1)求；
(2)若内角的角平分线交于点，且，求的面积的最小值.