数学八年级上册第一章 全等三角形1.3 探索三角形全等的条件优质课课件ppt

这是一份数学八年级上册第一章 全等三角形1.3 探索三角形全等的条件优质课课件ppt，共28页。PPT课件主要包含了学习目标，问题情境，∠AEC∠BFD，AE∥BF，新知探索，△AEC≌△BFD，△ADE≌△BCF，△ADC≌△BCD，ABCD已知，AEBF已知等内容，欢迎下载使用。

熟练运用“边角边”判定两个三角形全等，提高有条理地思考和说理能力.
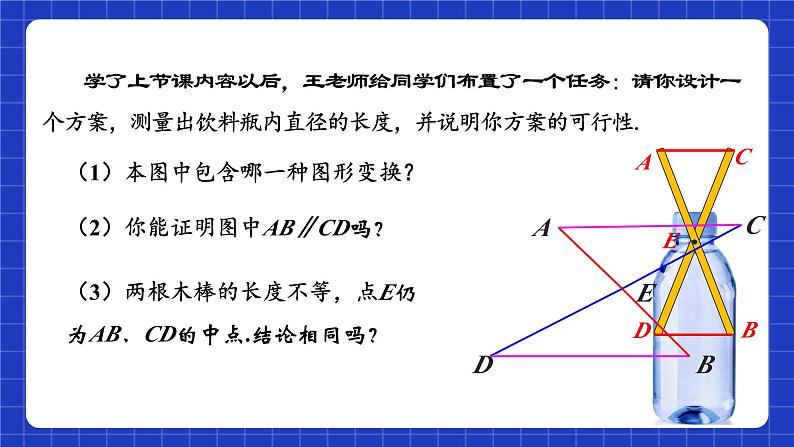
学了上节课内容以后，王老师给同学们布置了一个任务：请你设计一个方案，测量出饮料瓶内直径的长度，并说明你方案的可行性.
小明给出如下方案： 找两根长度相等的木棒，在中点处固定，按如图方法放置处于同一水平位置，测量出AC的长度即为塑料瓶内直径的长度．
你认为小明给出的方案合理吗？说出你的理由.
我认为小明给出的方案合理. 理由如下：
（1）本图中包含哪一种图形变换？
（2）你能证明图中AB∥CD吗？
（3）两根木棒的长度不等，点E仍为AB、CD的中点.结论相同吗？
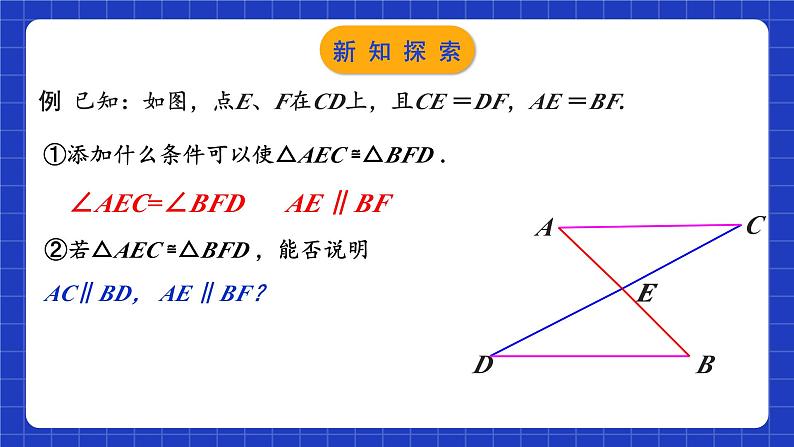
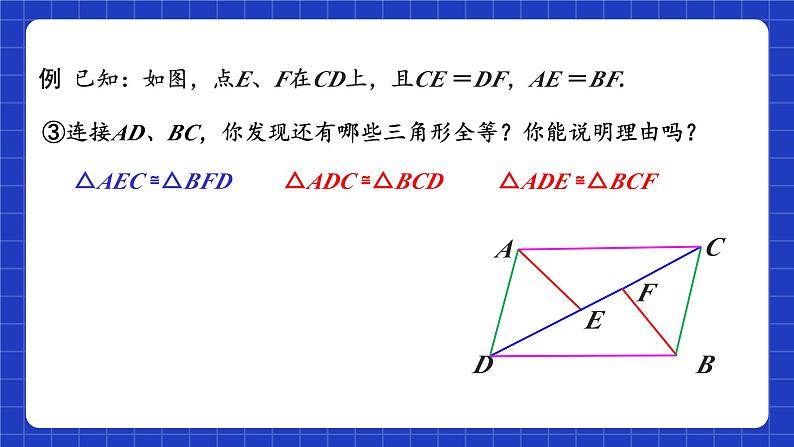
例 已知：如图，点E、F在CD上，且CE ＝DF，AE ＝BF.
①添加什么条件可以使△AEC ≌△BFD ．
②若△AEC ≌△BFD ，能否说明AC∥BD， AE ∥BF？
③连接AD、BC，你发现还有哪些三角形全等？你能说明理由吗？
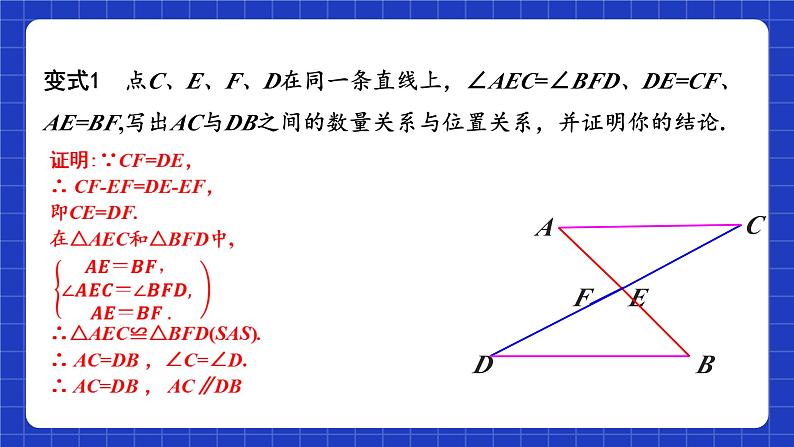
变式1 点C、E、F、D在同一条直线上，∠AEC=∠BFD、DE=CF、AE=BF,写出AC与DB之间的数量关系与位置关系，并证明你的结论.
变式2 如图，C是AE的中点，AB//CD，且AB=CD.求证： BC//DE ．
AC=CE （已证），
证明:∵点?是线段??的中点（已知），∴AC=CE （中点定义）.
∵ AB//CD （已知），∴ ∠A=∠DCE （两直线平行，同位角相等）.
在△ABC和△CDE中，
∴△ABC≌△CDE（SAS）.
∠A=∠DCE （已证），
∴ ∠ACB=∠CED（全等三角形的对应角相等），∴BC∥DE(同位角相等，两直线平行).
变式3 如图，点A、D、C、B在同一条直线上，AD=CB，AE=BF，AE∥BF.请探索CE与DF有怎样的位置关系？
AC=BD （已证），
证明:∵AE∥BF，∴∠A=∠B（两直线平行，内错角相等）.
∴ ∠ACE=∠BDF（全等三角形的对应角相等），∴CE∥DF(内错角相等，两直线平行).
又∵ AD=CB，∴ AD+DC=CB+DC,即AC=BD.
在△AEC和△DFB中，
∴△AEC≌△DFB（SAS），
∠A=∠B （已证），
①准备条件：证全等时要用的间接条件要先证好；
②指明范围：写出在哪两个三角形中；
③摆齐根据：摆出三个条件用大括号括起来；
④写出结论：写出全等结论.
1.如图，△ABC中， AB =AC，AD平分∠BAC .（1）求证：△ABD ≌ △ACD．（2）求证：AD⊥BC
证明:（2）∵△ABD≌△ACD，∴∠ADB=∠ADC.∵∠ADB+∠ADC=180°∴∠ADB=∠ADC=90°∴AD⊥BC
2. 如图，已知AB∥CD，AB＝CD，求证： AB∥CD ，AD＝BC．
1.下列条件中，能作出唯一三角形的是(　　 )A．已知三个角 B．已知两边和其中一边的对角C．已知三角形的周长 D．已知两边和它们的夹角
2.如图，OA=OB，OC=OD. 若∠D=35°,则∠C等于(　　)A.60° B.50° C.35°D.条件不够，无法求出
3.如图，OA＝OC，OB＝OD，OA⊥OB，OC⊥OD，有下列结论：①△AOD≌△COB；②CD＝AB；③∠CDA＝∠ABC．其中正确的是( ) A．①② B．①②③ C．①③ D．②③
4．如图，AB＝AD，∠BAD＝∠CAE ，如果增加一个条件_________，那么就可以根据“SAS”证明△ABC≌△ADE.
5.如图，AD=AE，∠1=∠2，BD=CE，则△ABE≌_________,判定依据是__________.
6．如图，AB＝CD，要判定△ABC≌△CDA，还需要的一个条件是___________________．
7. 如图，线段AD，CE相交于点B，BC＝BD，AB＝EB， 求证：△ACD≌△EDC．
8.如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C. 求证：AF=DE.
9.已知:如图，BE⊥CD于点E，BE=DE，AE=CE，DA的延长线交BC于点F.求证：DF⊥BC.
10. 如图，AD是△ABC的中线，在AD及其延长线上截取DE＝DF，连接CE，BF，△BDF与△CDE全等吗？BF与CE有何位置关系？请说明理由．
“倍长中线法”是解决几何问题的重要方法．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，具体做法是： 如图，AD是△ABC的中线，延长AD 到E ，使DE=AD，连接BE ，构造出△BED和△CAD .求证：△BED≌△CAD．
若AB=5， AC=3，则BC边上的中线AD的取值范围是__________.
解:∵△BED≌△CAD，∴AD=DE，BE=AC=3.在△AEB中，AB-BE＜AE＜AB+BE，即5-3＜2AD＜5+3，∴ 1＜AD＜4,∴AD的取值范围是1＜AD＜4.