

数学八年级上册1.3 探索三角形全等的条件获奖ppt课件
展开1.探索并掌握两个三角形全等的条件“ASA”;
2.能应用“ASA”判定两个三角形全等,并能运用“ASA”解决简单的实际问题;
3.体会观察、实验、猜想、归纳问题的方法,积累数学活动的经验.
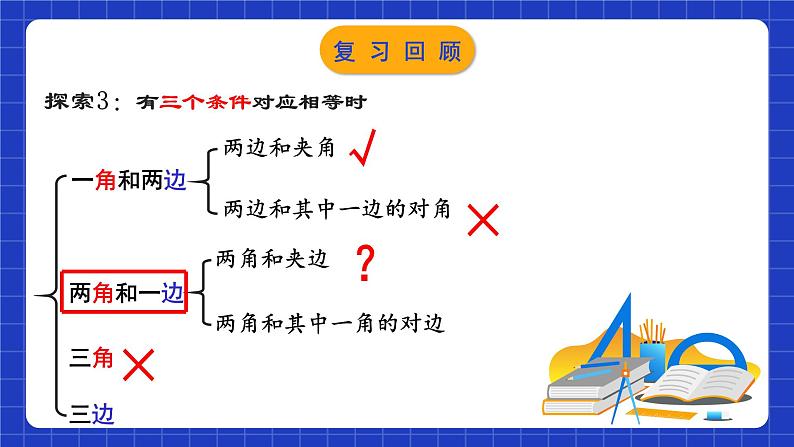
探索3:有三个条件对应相等时
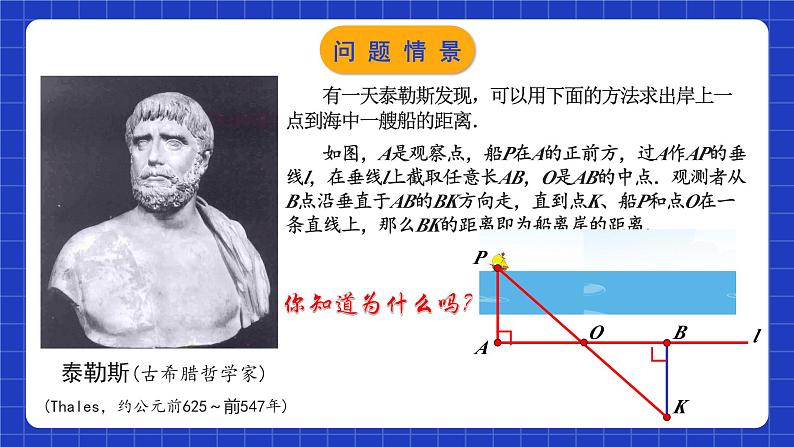
(Thales,约公元前625~前547年)
泰勒斯(古希腊哲学家)
有一天泰勒斯发现,可以用下面的方法求出岸上一点到海中一艘船的距离. 如图,A是观察点,船P在A的正前方,过A作AP的垂线l,在垂线l上截取任意长AB,O是AB的中点.观测者从B点沿垂直于AB的BK方向走,直到点K、船P和点O在一条直线上,那么BK的距离即为船离岸的距离.
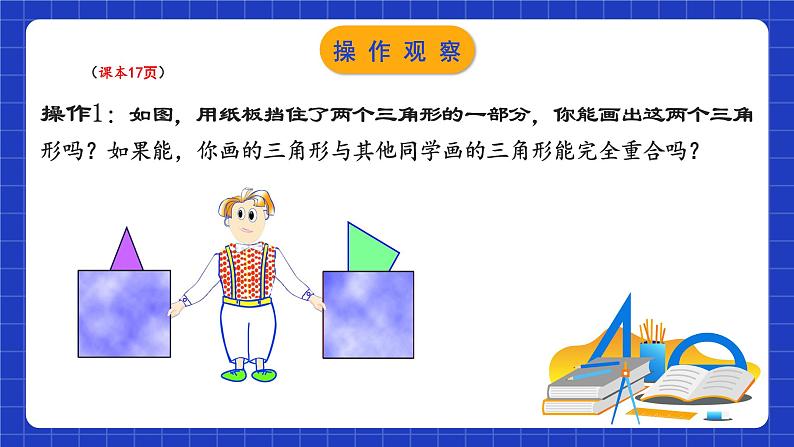
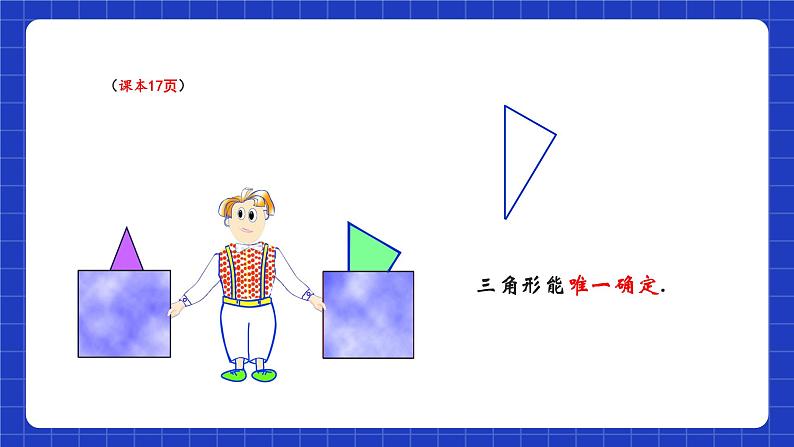
操作1:如图,用纸板挡住了两个三角形的一部分,你能画出这两个三角形吗?如果能,你画的三角形与其他同学画的三角形能完全重合吗?
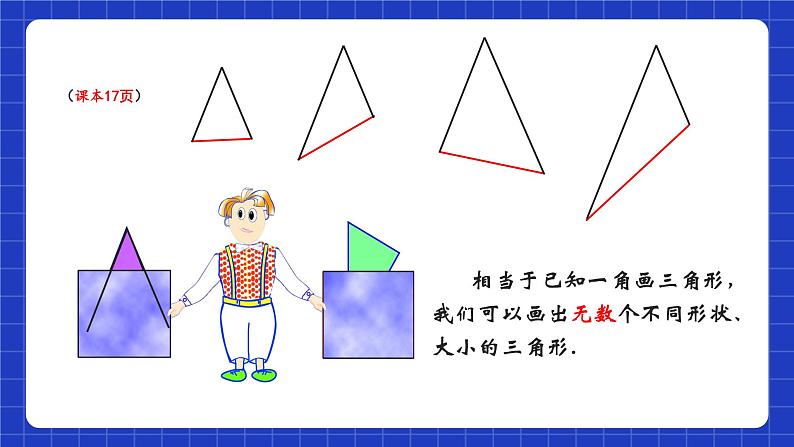
相当于已知一角画三角形,我们可以画出无数个不同形状、大小的三角形.
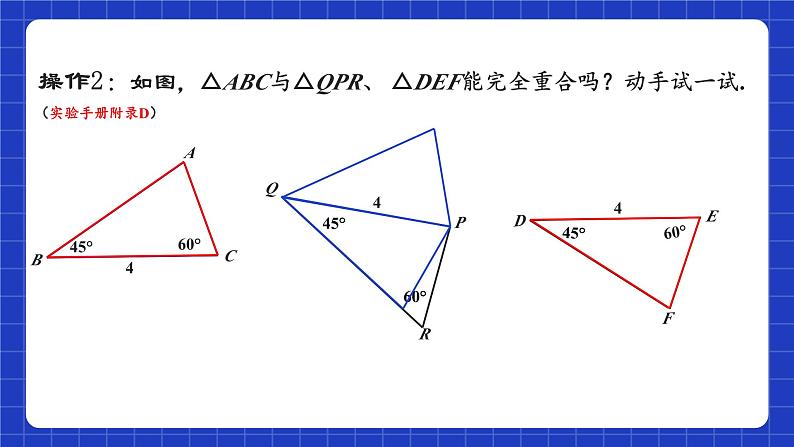
操作2:如图,△ABC与△QPR、 △DEF能完全重合吗?动手试一试.
操作3:按下列作法,用直尺和圆规作△ABC,使AB=a, ∠A=∠α, ∠B=∠β,
1你作的三角形与其他同学作的三角形能完全重合吗?你有什么发现?
作法:1.作AB=a.2.在AB的同一侧分别作∠MAB=∠α ,∠NBA=∠β ,AM、BN相交于点C.3.分别连接AB、AC.△ABC就是所求作的三角形.
以上实践告诉我们判定两个三角形全等的一个基本事实:
两角及其夹边分别相等的两个三角形全等.(简写成“角边角”或“ASA”)
1.找出图中的全等三角形,并说明理由.
你能说出理由了吗?试一试.
若AP∥BK,其它条件不变,结论仍然成立吗?
例 已知:如图,在△ABC中,D是BC的中点,点E、F分别在AB、AC上,且DE//AC,DF//AB.求证:BE=DF,DE=CF.
1.完成下列推理过程:
在△ABC和△DCB中,
∠ABC=∠DCB(已知)
∠ACB=∠DBC(已知)
( )
∴△ABC≌△DCB( )
2. 如图,AB=DC,∠B=∠C,欲证△ABF≌△DCE,需要添加条件 ,证明全等的理由是 .
3.如图,∠C=∠E,∠1=∠2,BA=DA,你能证明BC=DE吗?
4.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C
(1)求证:△ABE≌△ACD
∴△ACD≌△ABE(ASA)
(2) ∵△ACD≌△ABE(已证) ∴AD=AE(全等三角形的对应边相等) 又∵AB=AC(已知) ∴AB-AD=AC-AE(等式性质) ∴BD=CE
(2) BD和CE相等吗?
①公共角相等、对顶角相等、直角相等;
②等角加(减)等角,其和(差)相等;
③同角或等角的余(补)角相等;
④根据角平分线、平行线得角相等.
证明两个三角形全等时寻找等角的常用方法:
问:这位同学的回答及证明过程正确吗?为什么?
阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
解:这位同学的解法错误.因为两角夹边对应相等的两个三角形全等.本题中,∠A与∠AOD的夹边是OA,∠C与∠BOC的夹边是OC,因为OA≠OC,所以不能证明两三角形全等.
1. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就另外画出了一个与原来完全一样的三角形,这两个三角形全等的依据是____________.
2.如图,在用尺规作图得到△DBC≌△ABC过程中,先作∠DBC=∠ABC,再作∠DCB=∠ACB,从而得到△DBC≌△ABC,其中运用的三角形全等的判定方法是____________.
4.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ,才能使△ABC≌△DEF (写出一个即可).
5.下列判断正确的是 ( )A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等,且有一角为 30°的两个等腰三角形全等C.有两角及其夹边对应相等的两个三角形全等D.有两边和一角对应相等的两个三角形全等
6.如图,已知点?在△???的外部,点?在??边上,??交??于?,若 ∠?=∠?=∠?,??=??,则有( )
提示:由∠2=∠3可得∠C=∠E
7.如图,点B、E、C、F在同一条直线上,BC=EF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.
8.如图,E、F 在线段AC上,DF∥BE,AE=CF.若∠A =∠C, 求证:DF=BE.
9.点B、F、C、E在直线l上(点F、C之间不能直接测量),点A、D在l的异侧,AB∥DE、∠A=∠D,测得AB=DE.(1)求证:△ABC≌△DEF;(2)若BE=12 m,BF=4 m,求FC的长度.
解: (2)∵△ABC≌△DEF,∴BC=EF.∴BF+FC=EC+FC.∴BF=EC.∵BE=12 m,BF=4 m,∴FC=12-4-4=4(m).
八年级上册1.2 全等三角形一等奖课件ppt: 这是一份八年级上册<a href="/sx/tb_c17289_t3/?tag_id=26" target="_blank">1.2 全等三角形一等奖课件ppt</a>,共31页。PPT课件主要包含了学习目标,温故知新,全等三角形的概念,新知讲授,全等三角形的性质,观察与思考,符号语言,操作与思考,常见组合图形展示,新知归纳等内容,欢迎下载使用。
数学八年级上册第一章 全等三角形1.3 探索三角形全等的条件课文内容ppt课件: 这是一份数学八年级上册<a href="/sx/tb_c17288_t3/?tag_id=26" target="_blank">第一章 全等三角形1.3 探索三角形全等的条件课文内容ppt课件</a>,共21页。PPT课件主要包含了书写格式等内容,欢迎下载使用。
初中数学苏科版八年级上册第一章 全等三角形1.3 探索三角形全等的条件公开课ppt课件: 这是一份初中数学苏科版八年级上册第一章 全等三角形1.3 探索三角形全等的条件公开课ppt课件,共60页。PPT课件主要包含了3练习,数学活动等内容,欢迎下载使用。













