苏科版（2024）1.3 探索三角形全等的条件评优课课件ppt

这是一份苏科版（2024）1.3 探索三角形全等的条件评优课课件ppt，共29页。PPT课件主要包含了学习目标，知识回顾，AO＝BO，AAS，温故知新，CO＝DO，ACBD，ASA，∠AOC∠BOD，𝑪𝑶𝑫𝑶等内容，欢迎下载使用。
1.进一步掌握“边角边”、“角边角”和“角角边”判定三角形全等；
2.能灵活应用条件判定两个三角形全等，增强说理能力，进一步提高分析、解决问题的能力.
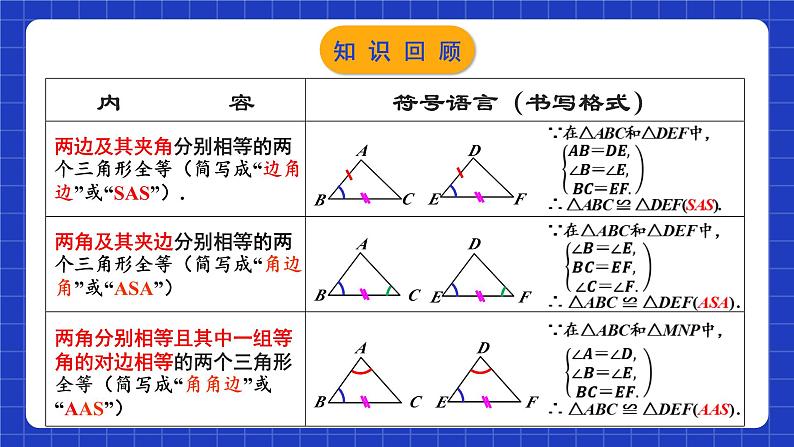
两边及其夹角分别相等的两个三角形全等（简写成“边角边”或“SAS”）.
两角及其夹边分别相等的两个三角形全等（简写成“角边角”或“ASA”）
两角分别相等且其中一组等角的对边相等的两个三角形全等（简写成“角角边”或“AAS”）
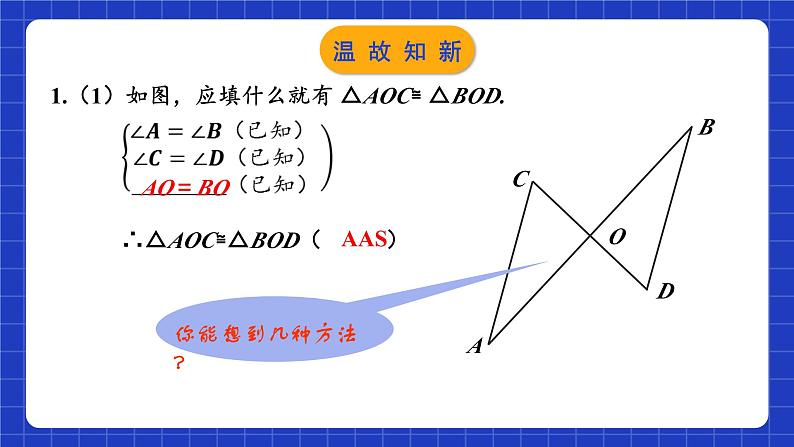
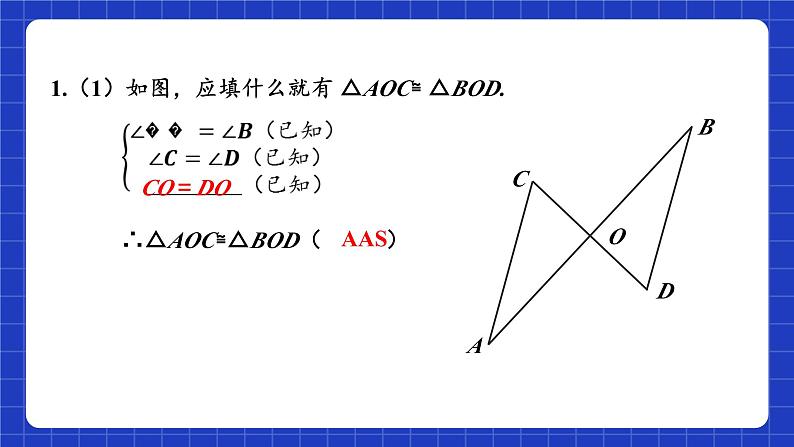
1.（1）如图，应填什么就有 △AOC≌ △BOD.
∴△AOC≌△BOD（ ）
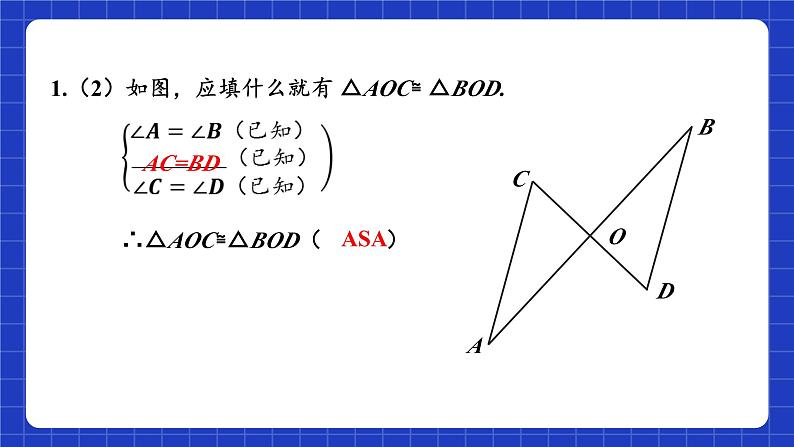
1.（2）如图，应填什么就有 △AOC≌ △BOD.
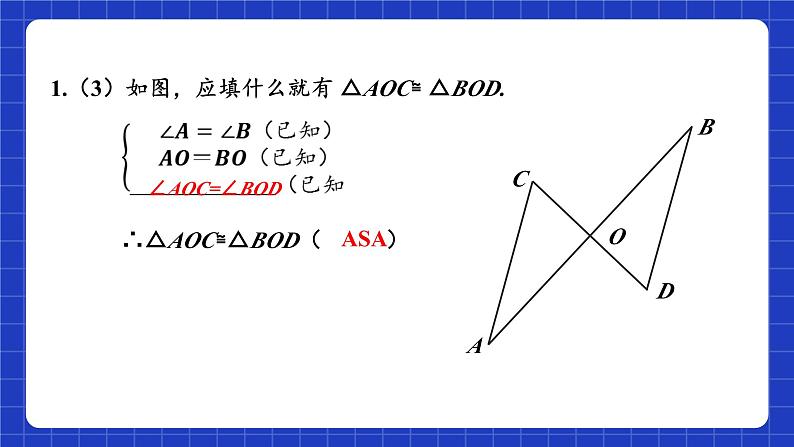
1.（3）如图，应填什么就有 △AOC≌ △BOD.
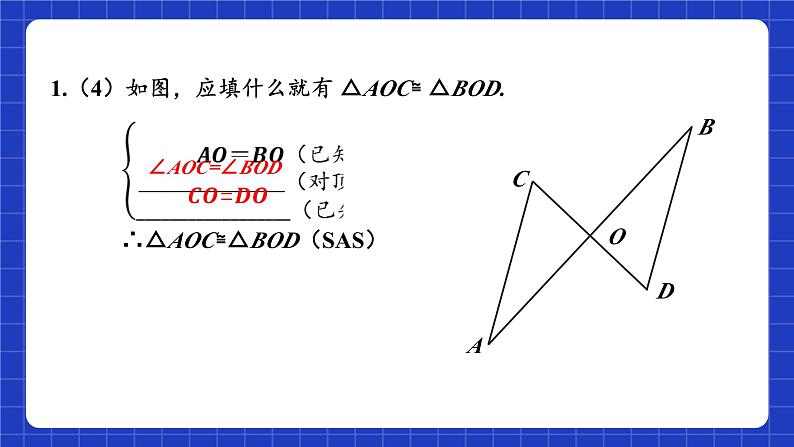
1.（4）如图，应填什么就有 △AOC≌ △BOD.
∴△AOC≌△BOD（SAS）
2. 如图，∠ABC＝∠DCB，要证明△ABC≌ △DCB，请添加 一个条件_________，依据是________.
1. 如图，∠A＝∠B， ∠1＝∠2， EA=EB，你能证明AC=BD吗？
2.如图，点C、F在AD上，且AF＝DC，∠B＝∠E，∠A＝∠D，你能证明AB＝DE吗?
例 已知：如图，点A、B、C、D在一条直线上，EA∥FB，EC∥FD，EA＝FB.求证：AB＝CD．
上面的推理过程可以用符号“”简明地表述如下：
1.已知：如图，AB＝AC，点D、E分别在AB、AC上，∠B＝∠C. 求证：DB＝EC .
∴△ABE≌△ACD（ASA）,
∴AE=AD（全等三角形对应边相等）.
∴AB-AD=AC-AE（等式性质）
2.已知：如图， ∠ABC＝∠DCB，∠1＝∠2 ， 求证：AB＝DC .
3. 如图，点A、B、C、D在同一条直线上，EA∥FD，EC∥FB，EA=FD. 求证：AB=CD. 本题推理过程如下: ⇒△ACE≌△DBF ⇒AC=DB⇒AC-BC=DB-BC⇒AB=CD 请你根据上述推理过程写出完整的证明过程.
(1)直接条件：即已知中直接给出的三角形的对应边或对应角．
证明三角形全等的“三类条件”:
(2)隐含条件：即已知没有给出，但通过读图得到的条件.
如：公共边、公共角、对顶角、直角相等.
(3)间接条件：即已知中所给条件不是三角形的对应边和对应角，需要 进一步推理．
①等边、等角加(减)等边、等角,其和(差)相等；
②同角或等角的余(补)角相等；
③根据角平分线、平行线得角相等,由中线的定义得边相等.
1．下列说法：①全等图形的形状相同、大小相等；②有两边和一角对应相等的两个三角形全等；③一个锐角和一条直角边对应相等的两个直角三角形全等；④全等三角形的对应边上的高相等；其中正确的说法为( )A．①②④B．①③④C．②③④D．①②③④
2. 如图，点B，D，C，F在同一直线上，AC=DE，AC∥DE，添加一个条件，不能得到△ABC≌△EFD的是( )
A．∠B=∠F B．BD=FC C．∠A=∠E D．AB=EF
3.如图，填空：（填SAS、ASA或AAS)(1)已知AD=AE，∠ADB=∠AEC，利用______可以判定△ABD≅△ACE；(2)已知OE=OD，OB=OC，利用______可以判定△BOE≅△COD；(3)已知∠BEC=∠CDB，∠BCE=∠CBD，利用_____可以判定△BCE≅△CBD．
4. 2022年冬季奥运会在我国北京举行，奥运健儿们敢于拼搏、善于拼搏，在奥运赛场上展现新时代中国运动员的精神风貌和竞技水平，请你添加一个条件，为奥运健儿设计一只与图1一样的鞋子，已知：AB=DF，∠ABC=∠DFE，写出可添加的条件并标明依据________________． (三个字母简写理由，写出一种情况即可)．
5.如图，已知AD平分∠BAC ，AB=AC ，则此图中全等三角形有______对．
提示：根据SAS推出△ABD≌△ACD，求出∠B＝∠C，BE＝CF，根据全等三角形的判定推出△BDE≌△CDF，△AED≌△AFD，△AFB≌△AEC即可.
6. 如图，在△ABC中，∠B＝∠C，点D，E，F分别在边AB，BC，AC上，且BD＝CE，∠DEF＝∠C．请找出图中的全等三角形，并证明你的发现．
7. 已知△ABN和△ACM的位置如图，∠1＝∠2，AB＝AC，AM＝AN．
求证：（1）∠M＝∠N．
证明：(1)∵∠1＝∠2，∴∠BAN＝∠CAM，又∵AB＝AC，AN＝AM，∴△ABN≌△ACM（SAS），∴∠M＝∠N.
证明：(2)∵△ABN≌△ACM，∴∠B＝∠C，又∵AB＝AC，∠1＝∠2，∴△ABD≌△ACE（ASA），∴BD＝CE.