苏科版（2024）八年级上册1.3 探索三角形全等的条件精品课件ppt

这是一份苏科版（2024）八年级上册1.3 探索三角形全等的条件精品课件ppt，共34页。PPT课件主要包含了学习目标，问题情景，操作思考，∵AB＝A′B′，∴∠B∠B′，讨论交流，新知归纳，新知应用，例题讲解，BCAD等内容，欢迎下载使用。

1. 探索并理解直角三角形全等的判定方法“HL” ；
2. 会用“HL”判定两个直角三角形全等.
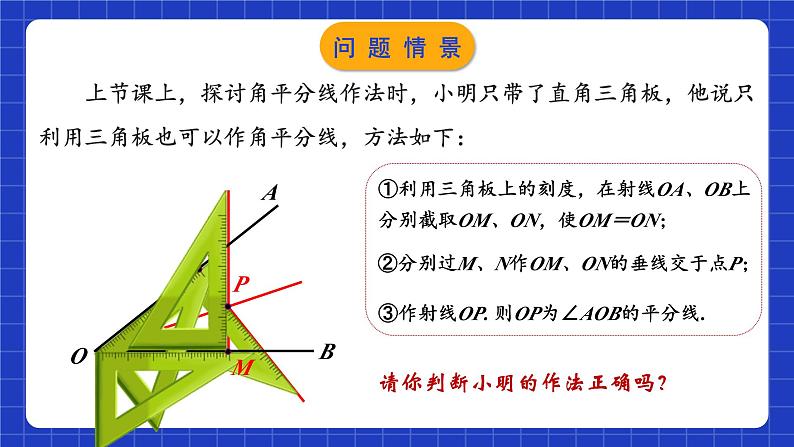
上节课上，探讨角平分线作法时，小明只带了直角三角板，他说只利用三角板也可以作角平分线，方法如下：
①利用三角板上的刻度，在射线OA、OB上分别截取OM、ON，使OM＝ON；
②分别过M、N作OM、ON的垂线交于点P；
③作射线OP. 则OP为∠AOB的平分线.
请你判断小明的作法正确吗？
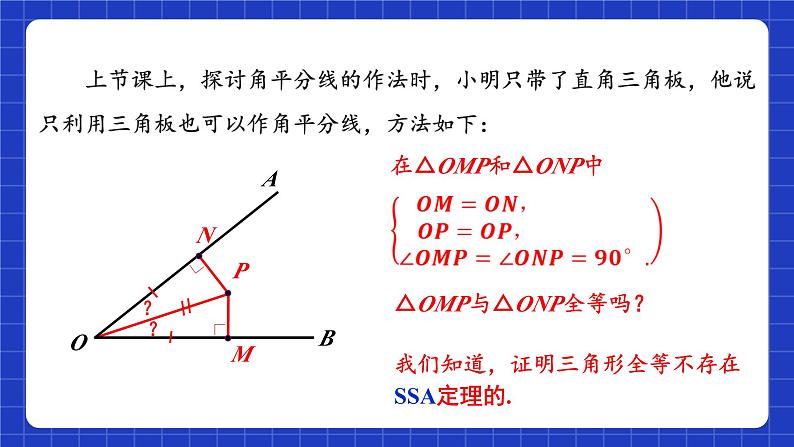
在△OMP和△ONP中
△OMP与△ONP全等吗？
上节课上，探讨角平分线的作法时，小明只带了直角三角板，他说只利用三角板也可以作角平分线，方法如下：
我们知道，证明三角形全等不存在SSA定理的.
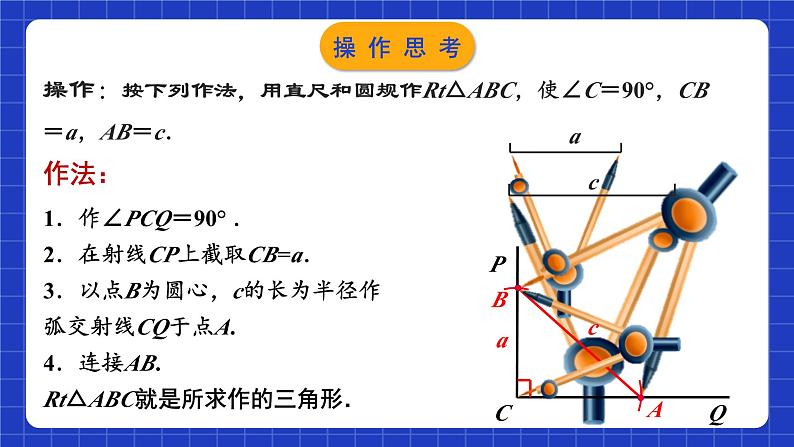
作法：1．作∠PCQ＝90° ．2．在射线CP上截取CB=a．3．以点B为圆心，c的长为半径作弧交射线CQ于点A.4．连接AB.Rt△ABC就是所求作的三角形．
操作：按下列作法，用直尺和圆规作Rt△ABC，使∠C＝90°，CB＝a，AB＝c．
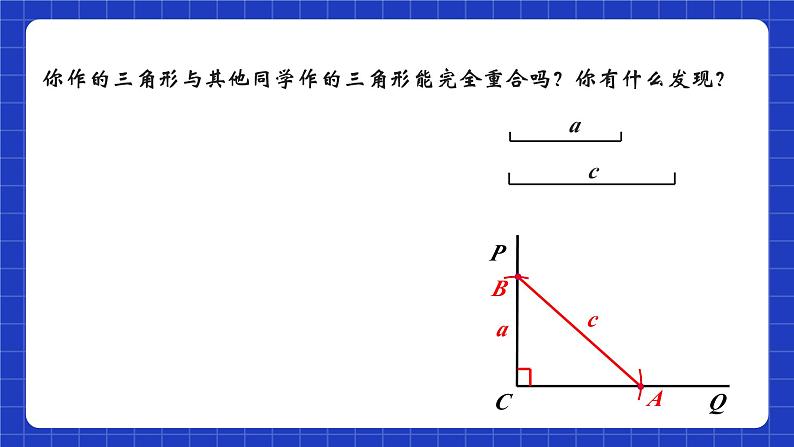
你作的三角形与其他同学作的三角形能完全重合吗？你有什么发现？
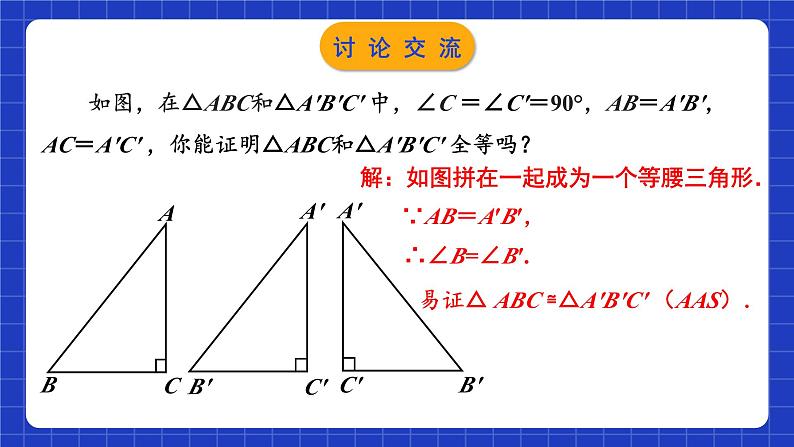
如图，在△ABC和△A′B′C′ 中，∠C ＝∠C′＝90°，AB＝A′B′， AC＝A′C′ ，你能证明△ABC和△A′B′C′ 全等吗？
解：如图拼在一起成为一个等腰三角形．
易证△ ABC ≌△A′B′C′ （AAS）．
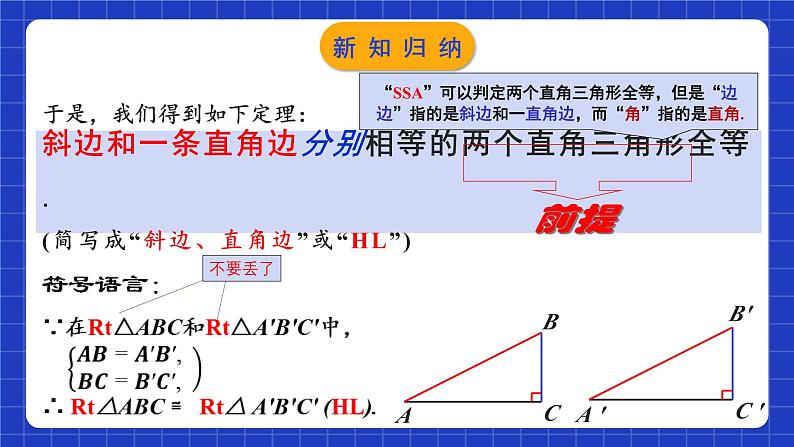
于是，我们得到如下定理：
斜边和一条直角边分别相等的两个直角三角形全等.(简写成“斜边、直角边”或“HL”)
如图，△ABC中，AB=AC，AD是高，则△ADB与△ADC_______(填“全等”或“不全等”)，根据_____（用简写法）.
注意“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
例 已知：如图，AD、BC相交于点O，AD=BC，∠C=∠D=90°,求证：①AC﹦BD.
利用全等证明两条线段相等，这是常见的思路.
例 已知：如图，AD、BC相交于点O，AD=BC，∠C=∠D=90°,求证：②AO﹦BO，CO=DO.
②证明：在△AOC 和△BOD 中，
∴△AOC≌△BOD(AAS)∴AO﹦BO，CO=DO(全等三角形对应边相等).
变式1 已知：如图，AD、BC相交于点O，AC=BD，∠C=∠D=90°,求证：AD﹦BC.
证明：在△AOC 和△BOD 中，
∴AO+DO﹦BO+CO (等式性质). 即AD=BC
变式2 如图，∠C=∠D=90°,要证明△ABC ≌△BAD，还需要什么条件？
（1） （ ）（2） （ ）（3） （ ） （4） （ ）
变式3 如图，∠C=∠D=90°,要证明△AOC≌△BOD，还需要什么条件？
（1） （ ）（2） （ ）（3） （ ）
1.在应用“HL”定理时，必须先得出两个_____三角形，然后证明__________________对应相等．
一般三角形与直角三角形全等的判定方法的比较：
2.判定两个三角形全等，至少要有一组对应边相等.
1.下列条件：①两条直角边对应相等；②斜边和一锐角对应相等；③斜边和一直角边对应相等;④直角边和一锐角对应相等.以上能判定两直角三角形全等的个数有 ( )A.1个 B.2个 C.3个 D.4个
2.如图，在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°，那么下列各条件中，不能使Rt△ABC和Rt△A′B′C′全等的是( )A.AB=A′B′=5，BC=B′C′=3 B.AB=B′C′=5，∠A=∠B′=40°C.AC=A′C′=5，BC=B′C′=3 D.AC=A′C′=5，∠A=∠A′=40°
3.如图，AB⊥BD，CD⊥DB，AD=BC.求证：AB=CD，AD//BC.
4.如图，已知AD，AF分别是两个钝角△ABC和△ABE的高，如果AD＝AF，AC＝AE. 求证：BC＝BE.
1.如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形全等的依据是( )A. AAS B. SSS C. HL D. SAS
2. 如图,BE=CF,AE⊥BC，DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF，则还需要添加一个条件是 ( )AE=DF B. ∠A=∠D C. ∠B=∠C D. AB=DC
3. 如图所示，BE⊥AC，CF⊥AB，垂足分别是E、F.若BE=CF，则图中全等三角形有( )A. 1对B. 2对C. 3对D. 4对
4.如图，AD=BC，AE⊥BD，CF⊥BD，垂足分别为E、F，且AE=CF，则图中相等的角(直角除外)有 ( )A. 3对B. 4对C. 5对D. 6对
5. 已知：如图，△ABC和△BAD中，∠C=∠D=90°，再添加一个条件_________________就可以判断△ABC≌△BAD．
6. 如图，已知AC⊥BD于点P，AP=CP，请增加一个条件，使△ABP≌△CDP(不能添加辅助线)．
(1)若以“SAS”为依据，则可添加条件___________;(2)若以“HL”为依据，则可添加条件___________ ;(3)若以“ASA”为依据，则可添加条件__________ ;(4)若以“AAS”为依据，则可添加条件___________．
7．如图，在四边形ABCD中，AB＝AD，CA平分∠BCD，AE⊥BC于点E，AF⊥CD交CD的延长线于点F.求证：△ABE≌△ADF.
8.如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF. 求证：BF=DE.
1.如图，已知AD，BC相交于点O，AB=CD，AM⊥BC于点M，DN⊥BC于点N，BN=CM．(1)求证：△ABM≌△DCN．
1.如图，已知AD，BC相交于点O，AB=CD，AM⊥BC于点M，DN⊥BC于点N，BN=CM．(2)试猜想OA与OD的大小关系，并说明理由．
2.有一Rt△ABC，∠C=90°，AC=10cm，BC=5cm，线段PQ=AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动，问P点运动到AC上什么位置时，△ABC才能和△APQ全等？