苏科版（2024）八年级上册第二章 轴对称图形2.5 等腰三角形的轴对称性精品课件ppt

这是一份苏科版（2024）八年级上册第二章 轴对称图形2.5 等腰三角形的轴对称性精品课件ppt，共38页。PPT课件主要包含了学习目标，知识回顾，探索与思考，证法1，你能证明你的结论吗，证法2，符号语言，新知归纳，在△ABC中，类比归纳等内容，欢迎下载使用。
1. 探索并证明等腰三角形的判定定理；
2. 探索等边三角形的性质定理和判定定理；
3. 会利用所学的定理进行说理.
定理1 等腰三角形的两底角相等. (简称“等边对等角”)．
定理2 等腰三角形底边上的高线、中线及顶角平分线重合. (简称“三线合一”)．
等腰三角形有哪些性质？
请说出“等腰三角形的两底角相等”这个命题的逆命题，并判断它是真命题还是假命题？
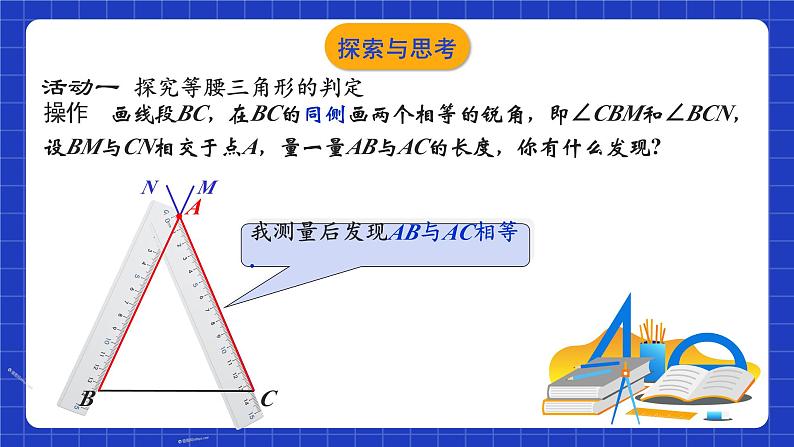
活动一 探究等腰三角形的判定
操作 画线段BC，在BC的同侧画两个相等的锐角，即∠CBM和∠BCN，设BM与CN相交于点A，量一量AB与AC的长度，你有什么发现?
我测量后发现AB与AC相等.
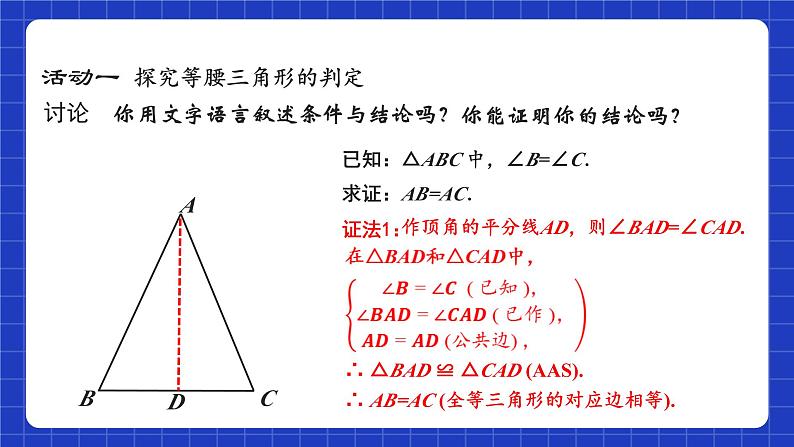
讨论 你用文字语言叙述条件与结论吗？
已知：△ABC 中，∠B=∠C．
作顶角的平分线AD，则∠BAD=∠CAD.
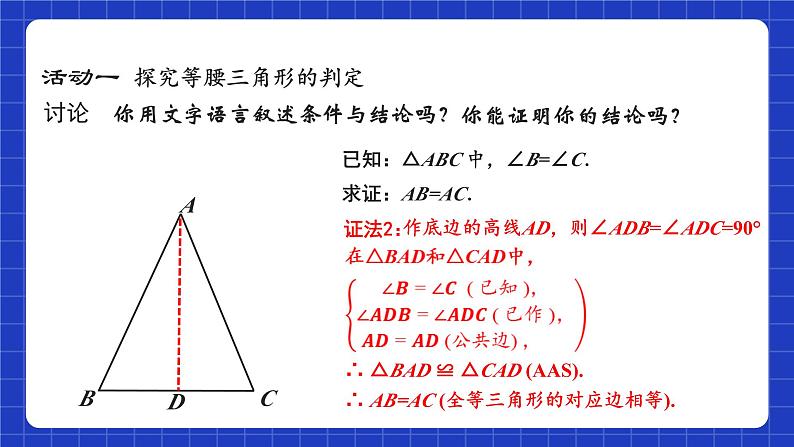
∴ △BAD ≌ △CAD (AAS).
∴ AB=AC (全等三角形的对应边相等).
作底边的高线AD，则∠ADB=∠ADC=90°
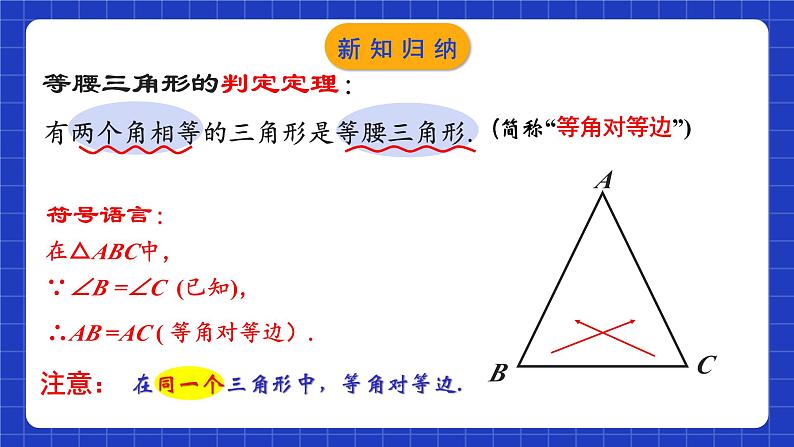
等腰三角形的判定定理：
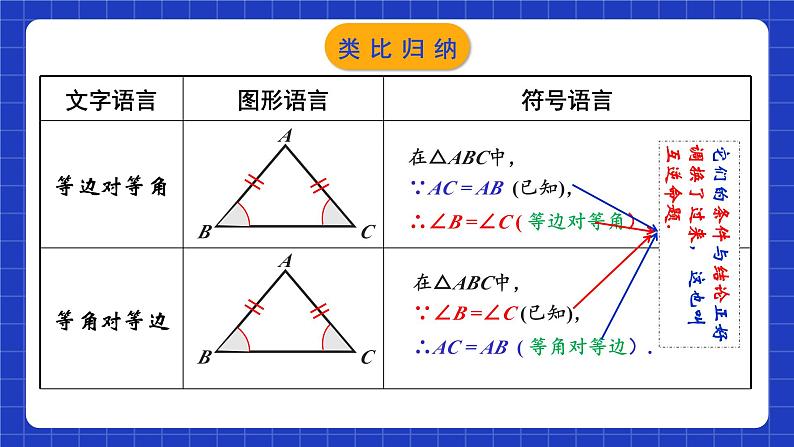
在△ABC中，∵∠B =∠C (已知)，
∴AB =AC ( 等角对等边）.
(简称“等角对等边”)
有两个角相等的三角形是等腰三角形.
在同一个三角形中，等角对等边.
∴∠B =∠C ( 等边对等角）.
∵AC = AB (已知)，
∴AC = AB ( 等角对等边）.
∵∠B =∠C (已知)，
它们的条件与结论正好调换了过来， 这也叫互逆命题.
1. 辨一辨：如图，下列推理正确吗?
解：错，因为都不是在同一个三角形中.
∵∠1=∠2, ∴ DC=BC（等角对等边）.
2. 在△ABC中，∠A和∠B的度数如下，其中能判定△ABC是等腰三角形的是(　　 )A.∠A=50°，∠B=70° B.∠A=70°，∠B=40°C.∠A=30°，∠B=90°D.∠A=80°，∠B=60°
3. 如图，在△ABC中，AB=AC，角平分线BD、CE相交于点O. OB与OC相等吗？请说明理由.
讨论1 什么是等边三角形？说说等边三角形与等腰三角形的关系.
活动二 探究等边三角形的性质
定义：三边相等的三角形叫做等边三角形或正三角形.
等边三角形是特殊的等腰三角形
讨论2 等边三角形的性质有哪些？请同学们说一说．
∵AB=AC， ∴∠B=∠C .(等边对等角) 同理 ∠A=∠C . ∴∠A=∠B=∠C. ∵ ∠A+∠B+∠C=180°, ∴ ∠A=∠B=∠C=60 °.
等腰三角形的两个底角相等.
等边三角形的三个角都相等，并且每一个角都等于60°.
等边三角形性质定理：等边三角形的每个内角都等于60°．
符号语言：∵△ABC是等边三角形∴ ∠A=∠B=∠C=60 °.
顶角的平分线、底边的高、底边的中线三线合一.
每条边上的中线,高和所对角的平分线都“三线合一”.
每一边上的中线、高和这一边所对的角的平分线互相重合(三条)
轴对称图形对称轴（3条）
轴对称图形对称轴（1条）
底边上的中线、高和顶角的平分线互相重合(1条)
例1 如图，已知△ABC为等边三角形，点E、F分别在边AC、BC上，且AE=CF，AF与BE相交于点D.(1)求证:△ABE≌△CAF;(2)求∠BDF的度数.
解：(1)证明:∵△ABC为等边三角形,∴∠BAE=∠C=60°，AB=CA，
∴△ABE≌△CAF (SAS).
解：(2)∵△ABE≌△CAF,∴∠ABE=∠CAF.∴∠BDF=∠ABE+∠BAF =∠CAF+∠BAF =∠BAC=60°.
1.等边三角形是轴对称图形，它的对称轴有( 　　)A. 1条 B. 2条 C. 3条 D. 以上都不对
2. 如图，△ABC是等边三角形，AD是BC边上的中线，AB=4，则BD=　　，∠BAD=　　　°. 
3.如图，在等边△ABC的AC边上取中点D，BC的延长线取一点E，使CE＝CD，连接BD，DE.求证：∠ABD＝∠E.
活动三 探究等边三角形的判定
讨论1 如果一个三角形的三个角都相等，那么这个三角形是等边三角形吗？为什么？
解：理由如下：如图，∵∠B=∠C， ∴AB=AC .(等角对等边) 同理 BC=AC . ∴AB=AC=BC.∴△ABC是等边三角形.
讨论2 有一个角是60°的等腰三角形是等边三角形吗？为什么？
解：理由如下：若顶角是60°，则两个底角相等，也都是60°. 所以三个角都相等，△ABC是等边三角形.若一个底角是60°，则另一个底角也是60°，顶角也是60°.所以三个角都相等，△ABC是等边三角形.
(1)三个角都相等的三角形是等边三角形.
等边三角形的判定定理：
(1)在△ABC中，∵∠A =∠B =∠C (已知)，
∴△ABC是等边三角形.
(2)有一个角是60°的等腰三角形是等边三角形．
(2)在△ABC中，∵∠A =60°(或∠B =60° 或∠C=60°
∴等腰△ABC是等边三角形.
三条边都相等的三角形是等边三角形
两个角相等的三角形是等腰三角形
三个角都相等的三角形是等边三角形
两条边相等的三角形是等腰三角形
有一个角是60°的等腰三角形是等边三角形.(等腰三角形法)
等边三角形判定方法归纳：
例2 如图,在等边三角形ABC中，DE∥BC，分别交AB、AC于点D、E .求证：△ADE是等边三角形.
证明：∵ △ABC是等边三角形，∴ ∠A= ∠B= ∠C.∵ DE//BC,∴ ∠ADE= ∠B=60°, ∠ AED= ∠C=60°.∴ ∠A= ∠ADE= ∠ AED=60°.∴ △ADE是等边三角形.
想一想：本题还有其他证法吗？
变式1 若点D、E 在边AB、AC 的延长线或反向延长线上，且 DE∥BC，结论还成立吗？
变式2：上题中，若将条件DE∥BC改为AD=AE， △ADE还是等边三角形吗？试说明理由.
∵ △ABC是等边三角形，
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
例3 如图，点C为线段AB上一点，△ACM与△CBN都是等边三角形．(1) 线段AN与线段BM是否相等？请说明理由；
解：(1)AN＝BM.理由：∵△ACM与△CBN都是等边三角形，∴AC＝MC，CN＝CB，∠ACM＝∠BCN＝60°.∴∠ACN＝∠MCB.∴△ACN≌△MCB(SAS)．∴AN＝BM.
(2) AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．
(2)△CEF是等边三角形．证明：∵∠ACE＝∠FCM=60°，∴∠ECF=60°.∵△ACN≌△MCB，∴∠CAE＝∠CMB.∵AC＝MC，∴△ACE≌△MCF(ASA)，∴CE＝CF.∴△CEF是等边三角形．
想一想：本题你还能得到哪些结论？
1.下列条件中，不能得到等边三角形的是(　　　)A．有两个内角是60°的三角形 B．三边都相等的三角形C．有一个角是60°的等腰三角形 D．有两个外角相等的等腰三角形
2.如图, 等边△ABC中, D、E、F分别是各边上的一点, 且AD=BE=CF．求证：△DEF是等边三角形．
证明：∵△ABC为等边三角形，且AD=BE=CF，∴AF=BD=CE，∠A=∠B=∠C=60°，∴△ADF≌△BED≌△CFE（SAS），∴DF=ED=EF，∴△DEF是等边三角形．
1.如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有(　　 )A．5个 B．4个 C．3个 D．2个
2. 如图，四边形ABCD是正方形，△PCD是等边三角形，连接BP，则∠BPC等于 ( )A. 15° B. 20° C. 25° D. 30°
3. 如图，等边三角形ABC的三条角平分线交于点O，DE∥BC，则这个图形中的等腰三角形共有 ( )
A. 4个 B. 5个 C. 6个 D. 7个
4.如图，在△ABC中，AB=AC，D是AB上一点，过D作DE⊥BC于点E，并与CA的延长线相交于点F，试判断△ADF的形状，并说明理由.
解：△ADF是等腰三角形.理由：在△ABC中.∵AB=AC，∴∠B=∠C.∵DE⊥BC，∴∠DEB=∠DEC=90°,∴∠BDE+∠B=90°，∠F+∠C=90°，∴∠BDE=∠F.∵∠BDE=∠ADF，∴∠ADF=∠F，∴AF=AD.∴△ADF是等腰三角形.
5. 如图，△ABC是等边三角形，E是AC上一点，D是BC延长线上一点，连接BE，DE，若∠ABE＝40°，BE＝DE，求∠CED的度数．
解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°.∵∠ABE＝40°，∴∠EBC＝∠ABC－∠ABE＝60°－40°＝20°.∵BE＝DE，∴∠D＝∠EBC＝20°，∴∠CED＝∠ACB－∠D＝40°.
6. 如图，△ABC是等边三角形，O为△ABC内任意一点，OE∥AB，OF∥AC，分别交BC于点E、F. 求证：△OEF是等边三角形.
证明:∵△ABC是等边三角形，∴∠B=∠C=60°.∵OE∥AB，OF∥AC，∴∠OEF=∠B=60°，∠OFE=∠C=60°.∵在△OEF中,∠O+∠OEF+∠OFE=180°,∴∠O=60°.∴∠O=∠OEF=∠OFE.∴△OEF是等边三角形.