2025届湖北省武汉市高新区数学九上开学综合测试试题【含答案】

这是一份2025届湖北省武汉市高新区数学九上开学综合测试试题【含答案】，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
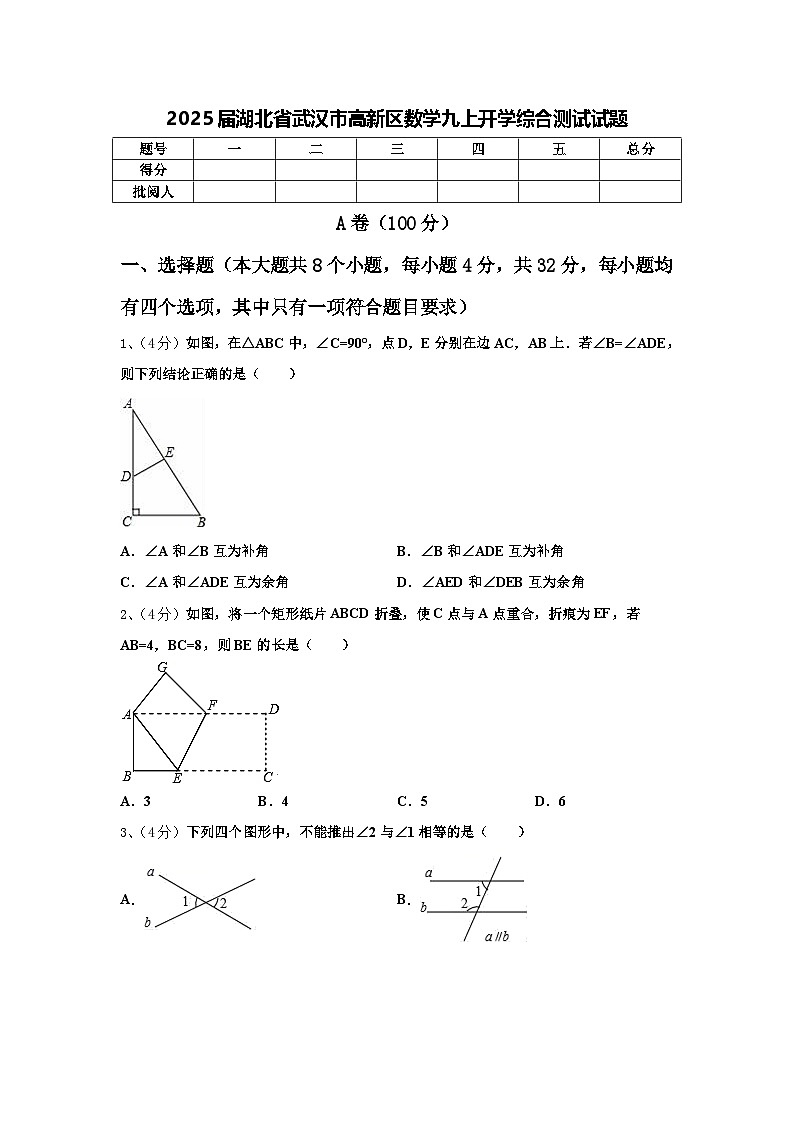
1、（4分）如图，在△ABC中，∠C=90°，点D，E分别在边AC，AB上．若∠B=∠ADE，则下列结论正确的是（ ）
A．∠A和∠B互为补角B．∠B和∠ADE互为补角
C．∠A和∠ADE互为余角D．∠AED和∠DEB互为余角
2、（4分）如图，将一个矩形纸片ABCD折叠，使C点与A点重合，折痕为EF，若AB=4，BC=8，则BE的长是（ ）
A．3B．4C．5D．6
3、（4分）下列四个图形中，不能推出∠2与∠1相等的是（ ）
A．B．
C．D．
4、（4分）下列式子：①y=3x﹣5；②y=；③y=；④y2=x；⑤y=|x|，其中y是x的函数的个数是（ ）
A．2个B．3个C．4个D．5个
5、（4分）下列分式中，是最简分式的是（ ）
A．B．C．D．
6、（4分）要使分式有意义，则x的取值应满足（ ）
A．x≠4B．x≠﹣1C．x＝4D．x＝﹣1
7、（4分）下列y关于x的函数中，是正比例函数的为（ ）
A．y＝x2B．y＝C．y＝D．y＝
8、（4分）矩形OABC在平面直角坐标系中的位置如图所示，已知，点A在x轴上，点C在y轴上，P是对角线OB上一动点（不与原点重合），连接PC，过点P作，交x轴于点D．下列结论：①；②当点D运动到OA的中点处时，；③在运动过程中，是一个定值；④当△ODP为等腰三角形时，点D的坐标为．其中正确结论的个数是（ ）
A．1个B．2个C．3个D．4个
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）已知为实数，且，则______.
10、（4分）某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图，则这组数据的中位数是_____．
11、（4分）关于 x 的方程 x2+5x+m＝0 的一个根为﹣2，则另一个根是________ ．
12、（4分）顺次连接矩形ABCD各边中点，所得四边形形状必定是__________．
13、（4分）若关于x的不等式组的解集为﹣＜x＜﹣6，则m的值是_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）某文具商店的某种毛笔每支售价25元，书法练习本每本售价5元，该商店为促销正在进行优惠活动：
活动1：买一支毛笔送一本书法练习本；
活动2：按购买金额的九折付款.
某学校准备为书法兴趣小组购买这种毛笔20支，书法练习本x（x≥20）本.
（1）写出两种优惠活动实际付款金额y1（元），y2（元）与x（本）之间的函数关系式；
（2）请问：该校选择哪种优惠活动更合算？
15、（8分）某中学形展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．
（1）根据图示填写下表：
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
（3）计算两班复赛成绩的方差．
16、（8分）如图，把两个大小相同的含有45º角的直角三角板按图中方式放置，其中一个三角板的锐角顶点与另一个三角板的直角顶点重合于点A，且B，C，D在同一条直线上，若AB＝2，求CD的长．
17、（10分）如图1，在正方形ABCD中，点E、F分别是边BC、CD上的点，且CE=CF，连接AE，AF，取AE的中点M，EF的中点N，连接BM，MN．
（1）请判断线段BM与MN的数量关系和位置关系，并予以证明．
（2）如图2，若点E在CB的延长线上，点F在CD的延长线上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
18、（10分）如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
（1）求证：四边形OCED是菱形；
（2）若点E到CD的距离为2，CD＝3，试求出矩形ABCD的面积．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，矩形纸片，，，点在边上，将沿折叠，点落在点处，，分别交于点，，且，则的值为_____________．
20、（4分）已知一次函数和函数,当时，x的取值范围是______________.
21、（4分）下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择_________．
22、（4分）农科院对甲、乙两种甜玉米各10块试验田进行试验后，得到甲、乙两个品种每公顷的平均产量相同，而甲、乙两个品种产量的方差分别为，，则产量较为稳定的品种是_____________（填“甲”或“乙”）．
23、（4分）把多项式因式分解成，则的值为________.
二、解答题（本大题共3个小题，共30分）
24、（8分）某公司调查某中学学生对其环保产品的了解情况，随机抽取该校部分学生进行问卷，结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型，分别记为，根据调查结果绘制了如下尚不完整的统计图.
（1）本次问卷共随机调查了名学生，扇形统计图中
（2）请根据数据信息，补全条形统计图；
（3）若该校有1000名学生，估计选择“非常了解”、“比较了解”共约有多少人？
25、（10分）已知，正方形ABCD中，点E为BC边上任意一点（点E不与B，C重合），点F在线段AE上，过点F的直线，分别交AB、CD于点M、N．
（1）如图，求证：；
（2）如图，当点F为AE中点时，连接正方形的对角线BD，MN与BD交于点G，连接BF，求证：；
（3）如图，在（2）的条件下，若，，求BM的长度.
26、（12分）解方程：
（1）＝2+；
（2）．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
试题分析：根据余角的定义，即可解答．
解：∵∠C=90°，
∴∠A+∠B=90°，
∵∠B=∠ADE，
∴∠A+∠ADE=90°，
∴∠A和∠ADE互为余角．
故选C．
考点：余角和补角．
2、A
【解析】
分析：根据翻折变换的性质可得AE=CE，设BE=x，表示出AE，然后在Rt△ABE中，利用勾股定理列方程求解即可．
详解：∵矩形纸片ABCD折叠C点与A点重合，
∴AE=CE，
设BE=x，则AE=8−x，
在Rt△ABE中,由勾股定理得,AB2+BE2=AE2，
即42+x2=(8−x)2，
解得x=3，
即BE=3.
故选A.
点睛：本题考查了翻折变换的性质，主要利用了翻折前后对应线段相等，难点在于利用勾股定理列出方程.
3、B
【解析】
根据平行线的性质以及对顶角相等的性质进行判断．
【详解】
解：A、∵∠1和∠2互为对顶角，
∴∠1＝∠2，故本选项错误；
B、∵a∥b，
∴∠1+∠2＝180°（两直线平行，同旁内角互补），
不能判断∠1＝∠2，故本选项正确；
C、∵a∥b，
∴∠1＝∠2（两直线平行，内错角相等），故本选项错误；
D、如图，
∵a∥b，
∴∠1＝∠3（两直线平行，同位角相等），
∵∠2＝∠3（对顶角相等），
∴∠1＝∠2，故本选项错误；
故选B．
本题考查了平行线的性质，解答本题的关键是掌握平行线的性质：两直线平行，同位角相等，内错角相等，同旁内角互补．
4、C
【解析】
根据函数的定义逐一进行判断即可得.
【详解】
①y=3x﹣5，y是x的函数；
②y=，y是x的函数；
③y=，y是x的函数；
④y2=x，当x取一个值时，有两个y值与之对应，故y不是x的函数；
⑤y=|x|，y是x的函数，
故选C．
本题考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．
5、D
【解析】
根据最简分式的定义：分子和分母没有公因式的分式，据此解答即可.
【详解】
A.=，故该选项不是最简分式，不符合题意，
B.==-1，故该选项不是最简分式，不符合题意，
C.==x+2，故该选项不是最简分式，不符合题意，
D.不能化简，是最简分式，符合题意.
故选D.
本题考查最简分式的定义，分子和分母没有公因式的分式叫做最简分式；最简分式首先系数要最简；一个分式是否为最简分式，关键看分子与分母是不是有公因式，但表面不易判断，应将分子、分母分解因式．
6、A
【解析】
根据分式有意义的条件列出关于x的不等式，求出x的取值范围即可．
【详解】
由题意知x-4≠0，
解得：x≠4，
故选：A．
本题考查的是分式有意义的条件，熟知分式有意义的条件是分母不等于零是解答此题的关键．
7、C
【解析】
试题解析：A、y是x的二次函数，故A选项错误；
B、y是x的反比例函数，故B选项错误；
C、y是x的正比例函数，故C选项正确；
D、y是x的一次函数，故D选项错误；
故选C．
考点：正比例函数的定义．
8、D
【解析】
①根据矩形的性质即可得到；故①正确；
②由点D为OA的中点，得到，根据勾股定理即可得到，故②正确；
③如图，过点P作于F，FP的延长线交BC于E，，则，根据三角函数的定义得到，求得，根据相似三角形的性质得到，根据三角函数的定义得到，故③正确；
④当为等腰三角形时，Ⅰ、，解直角三角形得到，
Ⅱ、OP＝OD，根据等腰三角形的性质和四边形的内角和得到，故不合题意舍去；
Ⅲ、，根据等腰三角形的性质和四边形的内角和得到，故不合题意舍去；于是得到当为等腰三角形时，点D的坐标为．故④正确．
【详解】
解：①∵四边形OABC是矩形，，
；故①正确；
②∵点D为OA的中点，
，
，故②正确；
③如图，过点P作 A于F，FP的延长线交BC于E，
，四边形OFEC是矩形，
，
设，则，
在中，，
，
，
，
，
，
，
，
，
，
，
，
，
，故③正确；
④，四边形OABC是矩形，
，
，
，
当为等腰三角形时，
Ⅰ、
Ⅱ、
，
，故不合题意舍去；
Ⅲ、，
，
故不合题意舍去，
∴当为等腰三角形时，点D的坐标为．故④正确，
故选：D．
考查了矩形的性质，锐角三角函数的定义，相似三角形的判定和性质，勾股定理，等腰三角形的性质，构造出相似三角形表示出CP和PD是解本题的关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、或.
【解析】
根据二次根式有意义的条件可求出x、y的值，代入即可得出结论．
【详解】
∵且，∴，∴，∴或．
故答案为：或．
本题考查了二次根式有意义的条件．解答本题的关键由二次根式有意义的条件求出x、y的值．
10、7.5
【解析】
根据中位数的定义先把数据从小到大的顺序排列，找出最中间的数即可得出答案.
【详解】
解：因图中是按从小到大的顺序排列的，最中间的环数是7环、8环，则中位数是=7.5（环）．
故答案为：7.5.
此题考查了中位数．注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求．如果是偶数个则找中间两位数的平均数.
11、
【解析】
解：设方程的另一个根为n，
则有−2+n=−5，
解得：n=−3.
故答案为
本题考查一元二次方程的两根是，则
12、菱形
【解析】
【分析】连接BD,AC,根据矩形性质和三角形中位线性质，可证四条边相等，可得菱形.
【详解】如图
连接BD,AC
由矩形性质可得AC=BD,
因为，E，F,G,H是各边的中点，
所以，根据三角形中位线性质可得：HG=EF=BD,EH=FG=AC
所以，EG=EF=EF=FG，
所以，所得四边形EFGH是菱形.
故答案为：菱形
【点睛】本题考核知识点：矩形性质，菱形判定. 解题关键点: 由三角形中位线性质证边相等.
13、1
【解析】
先解不等式组得出其解集为，结合可得关于的方程，解之可得答案．
【详解】
解不等式，得：，
解不等式，得：，
∵不等式组的解集为，
∴，
解得，
故答案为：1．
本题考查了解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1），；（1）买10支毛笔选择活动1，赠送10本练习本，剩下(x-10)本练习本选择活动1．
【解析】
（1）活动1：10支毛笔的付款金额，加上(x-10)本练习本的付款金额即可；活动1：将10支毛笔和x本练习本的总金额乘以0.9即可．
（1）可以任意选择一个优惠活动，也可两个活动同时选择，三种方案进行对比即可．
【详解】
（1）
（1）第三种方案：买10支毛笔选择活动1，赠送10本练习本，剩下(x-10)本练习本选择活动1，此时实际付款金额
显然
令，得
解得
因此当时，最优惠的购买方案为：买10支毛笔选择活动1，赠送10本练习本，剩下(x-10)本练习本选择活动1．
本题考查一次函数的应用，理解两种优惠活动的付款金额计算方式是解题的关键．
15、（1）九（1）的平均数为85，众数为85，九（2）班的中位数是80；（2）九（1）班成绩好些，分析见解析；（3）＝70，＝100
【解析】
（1）先根据条形统计图得出每个班5名选手的复赛成绩，然后平均数按照公式 ，中位数和众数按照概念即可得出答案；
（2）对比平均数和中位数，平均数和中位数大的成绩较好；
（3）按照方差的计算公式计算即可．
【详解】
解：（1）由图可知九（1）班5名选手的复赛成绩为：75、80、85、85、100，
九（2）班5名选手的复赛成绩为：70、100、100、75、80，
∴九（1）的平均数为（75＋80＋85＋85＋100）÷5＝85，
九（1）的众数为85，
把九（2）的成绩按从小到大的顺序排列为：70、75、80、100、100，
∴九（2）班的中位数是80；
（2）九（1）班成绩好些．因为两个班平均分相同，但九（1）班的中位数高，所以九（1）班成绩好些．
（3）＝＝70
＝＝100
本题主要考查数据的统计与分析，掌握平均数，中位数，众数和方差是解题的关键．
16、．
【解析】
过点A作AF⊥BC于F，先利用等腰直角三角形的性质求出BC=4，BF=AF=CF=2，再利用勾股定理求出DF，即可得出结论．
【详解】
如图，过点A作AF⊥BC于F，
在Rt△ABC中，∠B=45°，
∴△ABC是等腰直角三角形，
∴BC=AB=4，BF=AF=CF=BC=2，
∵两个同样大小的含45°角的三角尺，
∴AD=BC=4，
在Rt△ADF中，根据勾股定理得，DF=，
∴CD=DF-CF=，
故答案为：．
此题主要考查了勾股定理，等腰直角三角形的判定与性质，全等三角形的性质，正确作出辅助线是解本题的关键．
17、（1）BM=MN，BM⊥MN，证明见解析；（2）仍然成立，证明见解析
【解析】
（1）根据已知正方形ABCD的边角相等关系，推出△ABE≌△ADF(SAS)，得出AE=AF，利用MN是△AEF的中位线，BM为Rt△ABE的中线，可得BM=MN，由外角性质，得出∠BME=∠1+∠3，再由MN∥AF，∠1+∠2+∠EAF=∠BAD=90°，等角代换可推出结论；
（2）同（1）思路一样，证明△ABE≌△ADF(SAS)，利用外角性质和中位线平行关系，通过等角代换即得证明结论．
【详解】
（1）BM=MN，BM⊥MN．
证明：在正方形ABCD中，∠BAD=∠ABC=∠ADC=90°，AB=AD=BC=DC，
∵CE=CF，
∴BC-CE=DC-CF，
∴BE=DF，
∴△ABE≌△ADF(SAS)，
∴∠1=∠2，AE=AF，
∵M为AE的中点，N为EF的中点，
∴MN是△AEF的中位线，BM为Rt△ABE的中线．
∴MN∥AF，MN=AF，BM=AE=AM，
∴BM=MN，∠EMN=∠EAF，
∵BM=AM，
∴∠1=∠3， ∠2=∠3，
∴∠BME=∠1+∠3=∠1+∠2，
∴∠BMN=∠BME+∠EMN=∠1+∠2+∠EAF=∠BAD=90°，
∴BM⊥MN．
故答案为：BM=MN，BM⊥MN．

（2）（1）中结论仍然成立．
证明：在正方形ABCD中，∠BAD=∠ABC=∠ADC=90°，AB=AD=BC=DC，
∴∠ABE=∠ADF=90°，
∵CE=CF，∴CE-BC=CF-DC，∴BE=DF，
∴△ABE≌△ADF(SAS)，∴∠1=∠2，AE=AF，
同理（1）得MN∥AF，MN=AF，BM=AE=AM，
∴BM=MN，
同理（1）得∠BME=∠1+∠2，∠EMN=∠EAF，
∴∠BMN=∠EMN-∠BME=∠EAF-(∠1+∠2)=∠BAD=90°，
∴BM⊥MN，
故答案为：结论仍成立．
考查了正方形的性质，全等三角形的判定和性质，外角的性质，直角三角形中中线的性质，三角形中位线性质，熟记几何图形的性质概念是解题关键，注意图形的类比拓展．
18、（1）见解析；（2）矩形ABCD的面积＝1．
【解析】
（1）根据对边平行得四边形OCED是平行四边形，由原矩形对角线相等且互相平分得OC=OD，所以四边形OCED是菱形；
（2）根据三角形面积公式和矩形的面积等于4个△DEC的面积解答即可．
【详解】
（1）∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
∵四边形ABCD是矩形，
∴AC＝BD，OD＝BD，OC＝AC，
∴OC＝OD，
∴▱OCED是菱形；
（2）∵点E到CD的距离为2，CD＝3，
∴△DEC的面积＝ ，
∴矩形ABCD的面积＝4×3＝1．
本题考查了矩形的性质，是常考题型，难度不大；需要熟练掌握矩形、菱形的边、角、对角线的关系，不能互相混淆.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
由矩形的性质和已知条件，可判定,设，根据全等三角形的性质及矩形的性质可用含x的式子表示出DF和AF的长，在根据勾股定理可求出x的值，即可确定AF的值.
【详解】
解：四边形ABCD是矩形,
,,
是由沿折叠而来的
, ,
又
（AAS）

设,则
在中，根据勾股定理得：
,即
解得

故答案为：
本题考查了求多边形中的线段长，主要涉及的知识点有矩形的性质，全等三角形的判定与性质，勾股定理，数学的方程思想，用同一个字母表示出直角三角形中的三边长是解题的关键.
20、【解析】
作出函数图象，联立方程组，解出方程组，结合函数图象即可解决问题.
【详解】
根据题意画出函数图象得，
联立方程组和
解得，，,
结合图象可得，当时，故答案为：本题考查了一次函数的图象和一次函数图象上点的坐标特征．正确求出一次函数的交点是解题的关键．
21、丁；
【解析】
试题解析：丁的平均数最大，方差最小，成绩最稳当，
所以选丁运动员参加比赛.
故答案为丁.
22、乙
【解析】因为S甲2≈0.01＞S乙2≈0.002，方差小的为乙，所以本题中比较稳定的是乙．
23、
【解析】
根据多项式的乘法法则计算，然后即可求出m的值.
【详解】
∵=x2+6x+5，
∴m=6.
故答案为：6.
本题考查了因式分解，把一个多项式化成几个整式的乘积的形式，叫做因式分解.因式分解是乘法运算的逆运算.
二、解答题（本大题共3个小题，共30分）
24、（1）50； 32；（2）见解析；(3)560人.
【解析】
分析：（1）由条形统计图和扇形统计图可知，用“非常了解”的人数为8人除以所占比例为16％，即可求得总人数；“一般了解”的人数为16人除以总人数即可求所占比例；
（2）用总人数减去B、C、D部分的人数求出A部分的人数，然后补全条形统计图即可；
（3）先根据扇形统计图得到部分学生“非常了解”和“比较了解”的人数占样本总人数的比例，再由样本估计总体即可求解.
详解：（1）8÷16％=50人；
16÷50=32％.
（2）50-20-16-6=8人.如图，
（3）1000×（16％+40％）=560人.
点睛：本题考差了扇形统计图和条形统计图的综合，解答此类题目，要善于发现二者之间的关联点，即两个统计图都知道了那个量的数据，从而用条形统计图中的具体数量除以扇形统计图中占的百分比，求出样本容量，进而求解其它未知的量.
25、（1）见解析；（2）见解析；（3）.
【解析】
（1）由正方形的性质得出∠B=90°，得出∠BAE+∠AEB=90°，由垂直的性质得出∠BAE+∠AMN=90°，即可得出结论；
（2）连接AG、EG、CG，证明△ABG≌△CBG得出AG=CG，∠GAB=∠GCB，证出EG=CG，由等腰三角形的性质得出∠GEC=∠GCE，证出∠AGE=90°，由直角三角形斜边上的中线性质得出BF=AE，FG=AE，即可得出结论；
（3）过G作交AD于点P，交BC于点Q，证明DP=PG=2，连接ME，证明MN是AE的垂直平分线，得，，再证明得，得，进而得，中，由勾股定理得，代入相关数据，从而得出结论.
【详解】
（1）（1）证明：∵四边形ABCD是正方形，
∴∠B=90°，
∴∠BAE+∠AEB=90°，
∵MN⊥AE于F，
∴∠BAE+∠AMN=90°，
∴∠AEB=∠AMN；
（2）证明：连接AG、EG、CG，
∵四边形ABCD是正方形，
∴AB=BC，∠ABG=∠CBG=45°，∠ABE=90°，
在△ABG和△CBG中，
，
∴△ABG≌△CBG（SAS），
∴AG=CG，∠GAB=∠GCB，
∵MN⊥AE于F，F为AE中点，
∴AG=EG，
∴EG=CG，
∴∠GEC=∠GCE，
∴∠GAB=∠GEC，
∵∠GEB+∠GEC=180°，
∴∠GEB+∠GAB=180°，
∵四边形ABEG的内角和为360°，∠ABE=90°，
∴∠AGE=90°，
在Rt△ABE 和Rt△AGE中，AE为斜边，F为AE的中点，
∴BF=AE，FG=AE，
∴BF=FG；
（3）过G作交AD于点P，交BC于点Q，则 ，，
中，， ，
∴ ，
∴
∵，
∴ ，
∴ 即
连接ME ∵于F，F为AE的中点,
∴MN是AE的垂直平分线
∴，
由（2）知 ，，
∴，
又，
∴，
∴ ，
∴ ，
又，
∴
∴
∴
∵
∴四边形PDCQ为矩形
∴
设
∵E是BC中点
∴
∴
∴ 即
∴
∴
设
∴
中，由勾股定理得
∴ 解得
∴
本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、平行四边形的判定与性质、直角三角形斜边上的中线性质、勾股定理等知识；本题综合性强，有一定难度．
26、（1）x＝0；（1）x＝1．
【解析】
(1)两边同时乘以x-1，化为整式方程，解整式方程后进行检验即可；
(1)两边同时乘以3(x-3)，化为整式方程，解整式方程后进行验根即可得.
【详解】
(1)两边同时乘以x-1，得：
3x﹣5＝1(x﹣1)﹣x﹣1，
解得：x＝0，
检验：当x＝0时，x-1≠0，
所以x=0是分式方程的解；
(1)两边同时乘以3(x-3)，得
1x﹣1＝11x﹣11+x﹣3，
解得：x＝1，
检验：当x＝1时，3(x-3)≠0，
所以x=1是分式方程的解．
本题考查了解分式方程，熟练掌握解分式方程的一般方法以及注意事项是解题的关键.解分式方程要进行验根.
题号
一
二
三
四
五
总分
得分
批阅人
班级
平均数（分）
中位数（分）
众数（分）
九（1）
85
九（2）
85
100
甲
乙
丙
丁
平均数
9.14
9.15
9.14
9.15
方差
6.6
6.8
6.7
6.6