2025届湖北省襄阳市襄州区数学九上开学调研模拟试题【含答案】

这是一份2025届湖北省襄阳市襄州区数学九上开学调研模拟试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
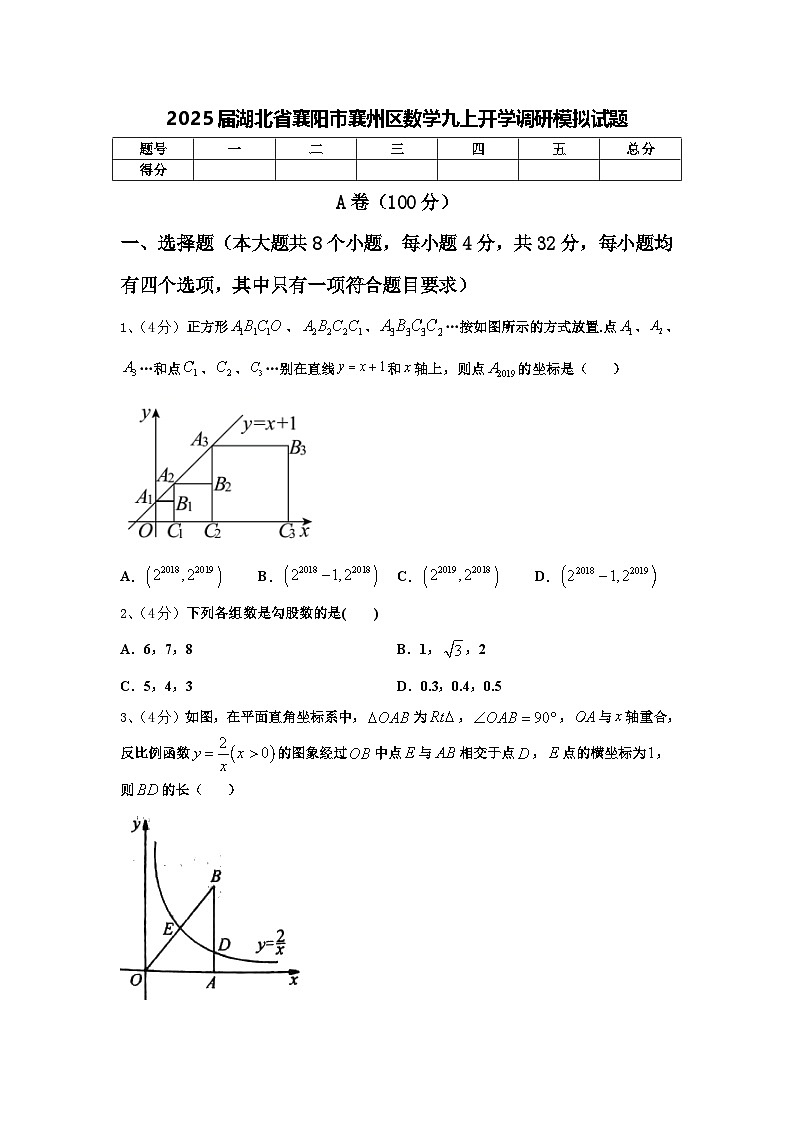
1、（4分）正方形、、…按如图所示的方式放置.点、、…和点、、…别在直线和轴上，则点的坐标是（ ）
A．B．C．D．
2、（4分）下列各组数是勾股数的是( )
A．6，7，8B．1，，2
C．5，4，3D．0.3，0.4，0.5
3、（4分）如图，在平面直角坐标系中，为，，与轴重合，反比例函数的图象经过中点与相交于点，点的横坐标为，则的长（ ）
A．B．C．D．
4、（4分）如图，四边形和四边形是以点为位似中心的位似图形，若，四边形的面积等于4，则四边形的面积为（ ）
A．3B．4C．6D．9
5、（4分）在平面直角坐标系中，点A的坐标为（﹣3，4），那么下列说法正确的是（ ）
A．点A与点B（﹣3，﹣4）关于y轴对称
B．点A与点C（3，﹣4）关于x轴对称
C．点A与点E（﹣3，4）关于第二象限的平分线对称
D．点A与点F（3，﹣4）关于原点对称
6、（4分）在平面直角坐标系中，将直线l1：y＝﹣2x﹣2平移后，得到直线l2：y＝﹣2x+4，则下列平移作法正确的是（ ）
A．将l1向右平移3个单位长度B．将l1向右平移6个单位长度
C．将l1向上平移2个单位长度D．将l1向上平移4个单位长度
7、（4分）如图，正方形ABCD的边长是3cm，一个边长为1cm的小正方形从图示位置开始，沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转，那么这个小正方形第2018次翻转到箭头与初始位置相同的方向时，小正方形所处的位置（ ）
A．在AB边上B．在BC边上C．在CD边上D．在DA边上
8、（4分）下列命题是假命题的是（ ）
A．两直线平行，同位角相等B．两组对角分别相等的四边形是平行四边形
C．若，则D．若，则
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）已知直角三角形的两条边为5和12，则第三条边长为__________．
10、（4分）如图，在等腰梯形 ABCD 中，AD∥BC，如果 AD＝4，BC＝8 ，∠B ＝60° ，那么这个等腰梯形的腰 AB 的长等于____．
11、（4分）一个有进水管和出水管的容器，从某时刻开始4 min内只进水不出水，在随后的8 min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y(L)与时间x(min)之间的关系如图所示，则每分钟的出水量为________________
12、（4分）若m2﹣n2=6，且m﹣n=2，则m+n=_________
13、（4分）正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则B5的坐标是_____________ 。
三、解答题（本大题共5个小题，共48分）
14、（12分）甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过1元后，超出1元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞1．
（1）根据题题意，填写下表（单位：元）
（2）当x取何值时，小红在甲、乙两商场的实际花费相同？
（3）当小红在同一商场累计购物超过1元时，在哪家商场的实际花费少？
15、（8分）某家电销售商城电冰箱的销售价为每台2100元，空调的销售价为每台1750元，每台电冰箱的进价比每台空调的进价多400元，商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等．
（1）求每台电冰箱与空调的进价分别是多少？
（2）现在商城准备一次购进这两种家电共100台，设购进电冰箱台，这100台家电的销售总利润为元，要求购进空调数量不超过电冰箱数量的2倍，试确定获利最大的方案以及最大利润．
16、（8分）在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为个单位长度，按要求作图：
①画出关于原点的中心对称图形；
②画出将绕点逆时针旋转得到
③请在网格内过点画一条直线将平分成两个面积相等的部分．
17、（10分）如图，在▱ABCD中，各内角的平分线分别相交于点E，F，G，H．
（1）求证：△ABG≌△CDE；
（2）猜一猜：四边形EFGH是什么样的特殊四边形？证明你的猜想；
（3）若AB=6，BC=4，∠DAB=60°，求四边形EFGH的面积．
18、（10分）如图，在ABCD中，点E，F分别在BC，AD上，且BE=FD，求证：四边形AECF是平行四边形．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）一次函数y＝mx﹣4中，若y随x的增大而减小，则m的取值范围是_____﹣
20、（4分）如图，在四边形ABCD中，∠DBC=90°，∠ABD=30°，∠ADB=75°，AC与BD交于点E，若CE=2AE=4，则DC的长为________．
21、（4分）如图，矩形ABCD的对角线AC与BD交于点O，过点O作BD的垂线分别交AD，BC于E，F两点．若AC=，∠AEO=120°，则FC的长度为_____．
22、（4分）已知一次函数（）经过点，则不等式的解集为__________．
23、（4分）分解因式：____．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．
（1）求证：四边形DEGF是平行四边形；
（2）当点G是BC的中点时，求证：四边形DEGF是菱形．
25、（10分）若关于的一元二次方程有实数根，．
（1）求实数的取值范围；
（2）设，求的最小值．
26、（12分）如图，四边形ABCD是正方形，E、F分别是AB和AD延长线上的点，BE＝DF，在此图中是否存在两个全等的三角形，并说明理由；它们能够由其中一个通过旋转而得到另外一个吗？简述旋转过程．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
利用一次函数图象上点的坐标特征及正方形的性质可得出点的坐标，根据点的坐标的变化可找出变化规律“点的坐标为（n为正整数）”，再代入n=2019即可得出的坐标，然后再将其横坐标减去纵坐标得到的横坐标，和的纵坐标相同．
【详解】
解：当时，，
∴点A1的坐标为（0，1）．
∵四边形A1B1C1O为正方形，
∴点B1的坐标为（1，1），点C1的坐标为（1，0）．
当时，，
∴点A2的坐标为（1，2）．
∵A2B2C2C1为正方形，
∴点B2的坐标为（3，2），点C2的坐标为（3，0）．
同理，可知：点B3的坐标为（7，4），点B4的坐标为（15，8），点B5的坐标为（31，16），…，
∴点的坐标为（n为正整数），
∴点的坐标为 ，
∴点的坐标为，即为 ．
故选：B．
本题考查了一次函数图象上点的坐标特征、正方形的性质以及规律型：点的坐标，根据点的坐标的变化找出变化规律是解题的关键．
2、C
【解析】
欲求证是否为勾股数，这里给出三边的长，只要验证即可．
【详解】
解：、，故此选项错误；
、不是整数，故此选项错误；
、，故此选项正确；
、0.3，0.4，0.5，勾股数为正整数，故此选项错误．
故选：．
本题考查了勾股数的概念，一般是指能够构成直角三角形三条边的三个正整数．验证两条较小边的平方和与最大边的平方之间的关系，从而作出判断．
3、B
【解析】
把E点的横坐标代入，确定E的坐标，根据题意得到B的坐标为（2，4），把B的横坐标代入求得D的纵坐标，就可求得AD，进而求得BD.
【详解】
解：反比例函数的图象经过OB中点E，E点的横坐标为1，
，
∴E（1，2），
∴B（2，4），
∵△OAB为Rt△，∠OAB=90°，
∴AB=4，
把x=2代入得，
∴AD=1，
∴BD=AB-AD=4-1=3，
故选：B．
此题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、三角形中位线性质，解题的关键是求得B、D的纵坐标．
4、D
【解析】
利用位似的性质得到AD：A'D'=OA：OA'=2：3，再利用相似多边形的性质得到得到四边形A'B'C'D'的面积.
【详解】
解：∵四边形ABCD和四边形A'B'C'D'是以点O为位似中心的位似图形，AD：A'D'=OA：04'=2：3，
∴四边形ABCD的面积：四边形A'B'C'D'的面积=4：9,
又∵四边形ABCD的面积等于4，
∴四边形A'B'C'D'的面积为9.
故选：D
本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫位似中心，注意：两个图形必须是相似形；对应点的连线都经过同一点；对应边平行（或共线）
5、D
【解析】
根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数；关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变；关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反；关于第二象限角平分线的对称的两点坐标的关系，纵横坐标交换位置且变为相反数可得答案．
【详解】
解：A、点A的坐标为（-3，4），∴则点A与点B（-3，-4）关于x轴对称，故此选项错误；
B、点A的坐标为（-3，4），∴点A与点C（3，-4）关于原点对称，故此选项错误；
C、点A的坐标为（-3，4），∴点A与点E（-3，4）重合，故此选项错误；
D、点A的坐标为（-3，4），∴点A与点F（3，-4）关于原点对称，故此选项正确；
故选D．
此题主要考查了关于xy轴对称点的坐标点的规律，以及关于原点对称的点的坐标特点，关键是熟练掌握点的变化规律，不要混淆．
6、A
【解析】
利用一次函数图象的平移规律，左加右减，上加下减，得出即可．
【详解】
∵将直线l1：y=-2x-2平移后，得到直线l2：y=-2x+4，
∴-2（x+a）-2=-2x+4，
解得：a=-3，
故将l1向右平移3个单位长度．
故选A．
此题主要考查了一次函数图象与几何变换，正确把握变换规律是解题关键．
7、C
【解析】
由正方形ABCD的边长是3cm，小正方形的边长为1cm，则小正方形在正方形ABCD每条边上翻转两次，每个直角处翻转一次，小正方形共翻转12次回到原来的位置，即可得到它的方向．
【详解】
∵正方形ABCD的边长是3cm，小正方形的边长为1cm，
∴小正方形在正方形ABCD每条边上翻转两次，每个直角处翻转一次，小正方形翻转12次回到原来的位置，
∴2018÷12＝它的方向为B选项所指的方向．
故选C．
本题主要利用正方形为背景考查了规律探索，解决这类问题的方法一般是先求解一部分情况，从特殊到一般而后发现规律拓展推广.
8、D
【解析】
根据平行线的性质、平行四边形的判定、实数的性质即可判断.
【详解】
A. 两直线平行，同位角相等，正确
B. 两组对角分别相等的四边形是平行四边形，正确
C. 若，则，正确
D. 若＞0，则，错误
故选D.
此题主要考查命题的真假，解题的关键是熟知根据平行线的性质、平行四边形的判定、实数的性质.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1或
【解析】
因为不确定哪一条边是斜边，故需要讨论：①当12为斜边时，②当12是直角边时，根据勾股定理，已知直角三角形的两条边就可以求出第三边．
【详解】
解：①当12为斜边时，则第三边==；
②当12是直角边时，第三边==1．
故答案为：1或.
本题考查了勾股定理的知识，难度一般，但本题容易漏解，在不确定斜边的时候，一定不要忘记讨论哪条边是斜边．
10、4
【解析】
过A作AE∥DC，可得到平行四边形AECD，从而可求得BE的长，由已知可得到△ABE是等边三角形，此时再求AB就不难求得了．
【详解】
借钱：过作AE∥DC,交BC于E，
在等腰梯形ABCD中,AD∥BC,
∴四边形AECD是平行四边形
∴AB=AE,CE=AD=4
∵∠B=60°，AB=AE,
∴△ABE是等边三角形，
∴AB=BE
∵BE=BC-EC=8-4=4
∴AB=4.
故答案为:4
本题考查平行四边形的性质和等边三角形的判定与性质.
11、L
【解析】
由前4分钟的进水量求得每分钟的进水量，后8分钟的进水量求得每分钟的出水量．
【详解】
前4分钟的每分钟的进水量为20÷4＝5，
每分钟的出水量为5－(30－20)÷8＝．
故答案为L．
从图象中获取信息，首先要明确两坐标轴的实际意义，抓住交点，起点，终点等关键点，明确函数图象的变化趋势，变化快慢的实际意义．
12、3
【解析】
利用平方差公式得到（m+n）（m-n）=6，然后把m-n=2代入计算即可．
【详解】
∵，
∴m＋n=3.
13、（31,16）
【解析】
首先由B1的坐标为（1，1），点B2的坐标为（3，2），可得正方形A1B1C1O1边长为1，正方形A2B2C2C1边长为2，即可求得A1的坐标是（0，1），A2的坐标是：（1，2），然后又待定系数法求得直线A1A2的解析式，由解析式即可求得点A3的坐标，继而可得点B3的坐标，观察可得规律Bn的坐标是（2n-1，2n-1）．
【详解】
∵B1的坐标为(1,1),点B2的坐标为(3,2)
∴正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2
∴A1的坐标是（0，1），A2的坐标是：（1，2）
设直线A1A2的解析式为：y=kx+b
∴
解得：
∴直线A1A2的解析式是：y=x+1
∵点B2的坐标为(3,2)
∴点A3的坐标为(3,4)
∴点B3的坐标为(7,4)
∴Bn的横坐标是：2n-1,纵坐标是：2n−1
∴Bn的坐标是(2n−1,2n−1)
故点B5的坐标为(31,16).
此题考查了待定系数法求解一次函数的解析式以及正方形的性质，在解题中注意掌握数形结合思想与方程思想的应用.
三、解答题（本大题共5个小题，共48分）
14、（1）表格见解析；（2）120；（3）当小红累计购物大于120时上没封顶，选择甲商场实际花费少；当小红累计购物超过1元而不到120元时，在乙商场实际花费少．
【解析】
（1）根据已知得出：
在甲商场：1+（290－1）×0.9=271，1+（290－1）×0.9x=0.9x+10；
在乙商场：20+（290－20）×0.92=278，20+（290－20）×0.92x=0.92x+2.2．
（2）根据题中已知条件，求出0.92x+2.2，0.9x+10相等，从而得出正确结论．
（3）根据0.92x+2.2与0.9x+10相比较，从而得出正确结论．
【详解】
解：（1）填表如下：
（2）根据题意得：0.9x+10=0.92x+2.2，
解得：x=120．
答：当x=120时，小红在甲、乙两商场的实际花费相同．
（3）由0.9x+10＜0.92x+2.2解得：x＞120，
由0.9x+10＞0.92x+2.2，解得：x＜120，
∴当小红累计购物大于120时上没封顶，选择甲商场实际花费少；
当小红累计购物超过1元而不到120元时，在乙商场实际花费少．
15、（1）每台空调进价为1600元，电冰箱进价为2000元；（2）当购进电冰箱34台，空调66台获利最大，最大利润为13300元．
【解析】
（1）设每台空调的进价为元，每台电冰箱的进价为元，根据题意可列出分式方程，故可求解；
（2）先表示出y，再求出x的取值，根据一次函数的性质即可求解．
【详解】
解：（1）设每台空调的进价为元，每台电冰箱的进价为元．
根据题意得，
解得，，
故每台空调进价为1600元，电冰箱进价为2000元．
（2）设购进电冰箱台，则进购空调（100-x）台，
∴，
∵购进空调数量不超过电冰箱数量的2倍，
∴100-x≤2x
解得，
∵为正整数，，，
∴随的增大而减小，
∴当时，的值最大，即最大利润，（元），
故当购进电冰箱34台，空调66台获利最大，最大利润为13300元．
此题主要考查一次函数与分式方程的求解，解题的关键是根据题意得到方程或函数进行求解．
16、（1）作图见解析 （2）作图见解析 （3）作图见解析
【解析】
（1）根据中心对称的性质作图即可．
（2）根据旋转的性质作图即可．
（3）根据三角形面积公式作图即可．
【详解】
（1）如图所示，即为所求．
（2）如图所示，即为所求．
（3）如图所示，直线CD即为所求．
本题考查了方格作图的问题，掌握中心对称的性质、旋转的性质、三角形面积公式是解题的关键．
17、（1）证明见解析；（2）矩形；（3）．
【解析】
试题分析：（1）根据角平分线的定义以及平行四边形的性质，即可得到AB=CD，∠BAG=∠DCE，∠ABG=∠CDE，进而判定△ABG≌△CDE；
（2）根据角平分线的定义以及平行四边形的性质，即可得出∠AGB=90°，∠DEC=90°，∠AHD=90°=∠EHG，进而判定四边形EFGH是矩形；
（3）根据含30°角的直角三角形的性质，得到BG，AG，BF，CF，进而得出EF和GF的长，可得四边形EFGH的面积．
试题解析：解：（1）∵GA平分∠BAD，EC平分∠BCD，∴∠BAG=∠BAD，∠DCE=∠DCB，∵▱ABCD中，∠BAD=∠DCB，AB=CD，∴∠BAG=∠DCE，同理可得，∠ABG=∠CDE，在△ABG和△CDE中，∵∠BAG=∠DCE，AB=CD，∠ABG=∠CDE，∴△ABG≌△CDE（ASA）；
（2）四边形EFGH是矩形．
证明：∵GA平分∠BAD，GB平分∠ABC，∴∠GAB=∠BAD，∠GBA=∠ABC，∵▱ABCD中，∠DAB+∠ABC=180°，∴∠GAB+∠GBA=（∠DAB+∠ABC）=90°，即∠AGB=90°，同理可得，∠DEC=90°，∠AHD=90°=∠EHG，∴四边形EFGH是矩形；
（3）依题意得，∠BAG=∠BAD=30°，∵AB=6，∴BG=AB=3，AG==CE，∵BC=4，∠BCF=∠BCD=30°，∴BF=BC=2，CF=，∴EF=﹣=，GF=3﹣2=1，∴矩形EFGH的面积=EF×GF=．
点睛：本题主要考查了平行四边形的性质，矩形的判定以及全等三角形的判定与性质的运用，解题时注意：有三个角是直角的四边形是矩形．在判定三角形全等时，关键是选择恰当的判定条件．
18、证明：在ABCD中，AD=BC且AD∥BC，
∵BE=FD，∴AF=CE．
∴四边形AECF是平行四边形
【解析】
试题分析：根据平行四边形的性质可得AF∥EC．AF=EC，然后根据平行四边形的定义即可证得．
证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵点E，F分别是BC，AD的中点，
∴，，
∴AF∥EC，AF=EC，
∴四边形AECF是平行四边形．
【点评】本题考查了平行四边形的性质与判定；熟练掌握平行四边形的性质，证出AF=EC是解决问题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、m＜1
【解析】
利用一次函数图象与系数的关系列出关于m的不等式m＜1即可．
【详解】
∵一次函数y＝mx﹣4中，y随x的增大而减小，
∴m＜1，
故答案是：m＜1．
本题主要考查一次函数图象与系数的关系．解答本题的关键是注意理解：k＞1时，直线必经过一、三象限，y随x的增大而增大；k＜1时，直线必经过二、四象限，y随x的增大而减小．
20、
【解析】
过A点作A⊥BD于F，根据平行线的判定可得AF∥BC，根据含30度直角三角形的性质可得BC=AB，根据三角形内角和可得∠ADB=∠BAD，根据等腰三角形的性质可得BD=AB，从而得到BC=BD，在Rt△CBE中，根据含30度直角三角形的性质可得BC，在Rt△CBD中，根据等腰直角三角形的性质可得CD．
【详解】
过A点作A⊥BD于F，
∵∠DBC=90°，
∴AF∥BC，
∵CE=2AE，
∴AF=BC，
∵∠ABD=30°，
∴AF=AB，
∴BC=AB，
∵∠ABD=30°，∠ADB=75°，
∴∠BAD=75°，∠ACB=30°，
∴∠ADB=∠BAD，
∴BD=AB，
∴BC=BD，
∵CE=4，
在Rt△CBE中，BC=CE=6，
在Rt△CBD中，CD=BC=6．
故答案为：6．
此题考查了含30度直角三角形的性质，以及等腰三角形的判定和性质，得到Rt△CBE是含30度直角三角形，以及Rt△CBD是等腰直角三角形是解本题的关键．
21、1
【解析】
先根据矩形的性质，推理得到OF=CF，再根据Rt△BOF求得OF的长，即可得到CF的长．
【详解】
解：∵EF⊥BD，∠AEO=120°，
∴∠EDO=30°，∠DEO=60°，
∵四边形ABCD是矩形，
∴∠OBF=∠OCF=30°，∠BFO=60°，
∴∠FOC=60°-30°=30°，
∴OF=CF，
又∵Rt△BOF中，BO=BD=AC=，
∴OF=tan30°×BO=1，
∴CF=1，
故答案为：1．
本题考查矩形的性质以及解直角三角形的运用，解题关键是掌握：矩形的对角线相等且互相平分．
22、
【解析】
先把（-1，0）代入y=kx+b得b=k，则k（x-3）+b＜0化为k（x-3）+k＜0，然后解关于x的不等式即可．
【详解】
解：把（-1，0）代入y=kx+b得-k+b=0，解b=k，
则k（x-3）+b＜0化为k（x-3）+k＜0，
而k＜0，
所以x-3+1＞0，
解得x＞1．
故答案为x＞1．
本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合.
23、（3x＋1）2
【解析】
原式利用完全平方公式分解即可．
【详解】
解：原式＝（3x＋1）2，
故答案为：（3x＋1）2
此题考查了因式分解−运用公式法，熟练掌握完全平方公式是解本题的关键．
二、解答题（本大题共3个小题，共30分）
24、证明见详解.
【解析】
（1）求出平行四边形AGCD，推出CD=AG，推出EG=DF，EG∥DF，根据平行四边形的判定推出即可.
（2）连接DG，求出∠DGC=90°，求出DF=GF，根据菱形的判定推出即可.
【详解】
（1）∵AG∥DC，AD∥BC，
∴四边形AGCD是平行四边形
∴AG=DC
∵E、F分别为AG、DC的中点，
∴GE=AG，DF=DC，
即GE=DF，GE∥DF
∴四边形DEGF是平行四边形
（2）连接DG，
∵四边形AGCD是平行四边形，
∴AD=CG
∵G为BC中点，
∴BG=CG=AD
∵AD∥BG，
∴四边形ABGD是平行四边形
∴AB∥DG
∵∠B=90°，
∴∠DGC=∠B=90°
∵F为CD中点，
∴GF=DF=CF，
即GF=DF
∵四边形DEGF是平行四边形，
∴四边形DEGF是菱形.
25、（1）k≤−2；（2）t的最小值为−1．
【解析】
（1）由一元二次方程存在两实根，可得△≥0，进而求得k的取值范围；
（2）将α+β化为关于k的表达式，根据k的取值范围得出t的取值范围，即可求得的最小值．
【详解】
（1）∵一元二次方程x2−2(2−k)x+k2+12=0有实数根a，β，
∴△≥0，即：1(2−k)2−1(k2+12)≥0，解得：k≤−2；
（2）由根与系数的关系得：a+β=−[−2(2−k)]=1−2k，
∴==−2，
∵k≤−2，
∴−2≤