初中华东师大版（2024）3. 相似三角形的性质图文课件ppt

这是一份初中华东师大版（2024）3. 相似三角形的性质图文课件ppt，共16页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点等内容，欢迎下载使用。

相似三角形的判定定理 2 判定定理 2 的应用
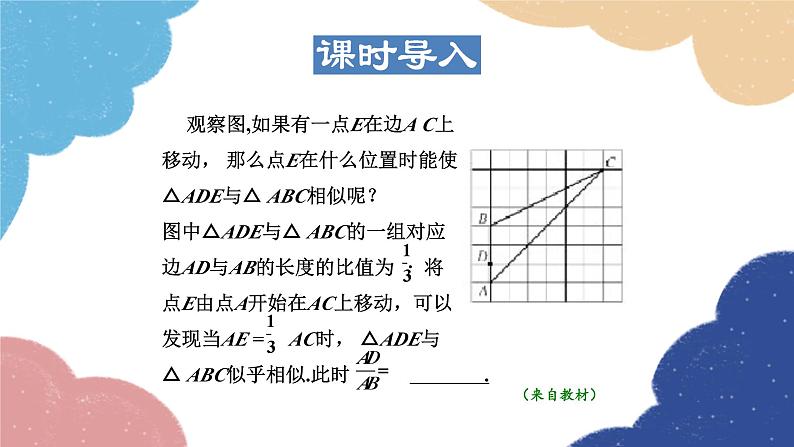
观察图,如果有一点E在边A C上移动， 那么点E在什么位置时能使△ADE与△ ABC相似呢？ 图中△ADE与△ ABC的一组对应边AD与AB的长度的比值为 将点E由点A开始在AC上移动，可以发现当AE = AC时， △ADE与△ ABC似乎相似.此时 .
相似三角形的判定定理 2
如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似.
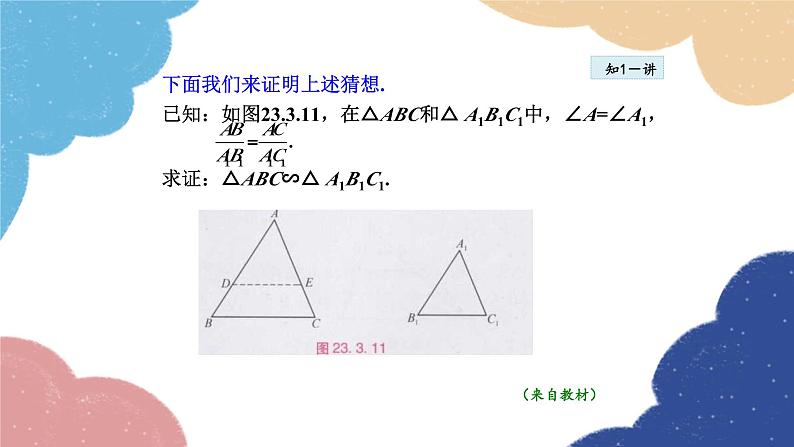
下面我们来证明上述猜想.已知：如图，在△ABC和△ A1B1C1中，∠A=∠A1， 求证：△ABC∽△ A1B1C1.
证明： 在边AB或它的延长线上截取AD=A1B1， 过点D作BC的平行线交AC于点E,则 △ADE∽△ABC∴ AE= A1C1.在△ADE与△A1B1C1 中，∵ AD=A1B1 ,∠A=∠A1， AE= A1C1 ，∴ △ADE≌△A1B1C1.∴△ABC∽△A1B1C1 .
相似三角形的判定定理2 两边成比例且夹角相等 的两 个三角形相似.数学表达式：在△ABC与△A′B′C′中， 且∠A＝∠A′ ∴△ABC∽△A′B′C′.
如果相等的角 不是成比例的两边的夹角，那么这两个 三角形还相似吗？画一画，看看是否不一定相似.
易错警示：运用该定理证明相似时，一定要注意边角的关系，角一定是两组对应边的夹角．类似于判定三角形全等的SAS方法．
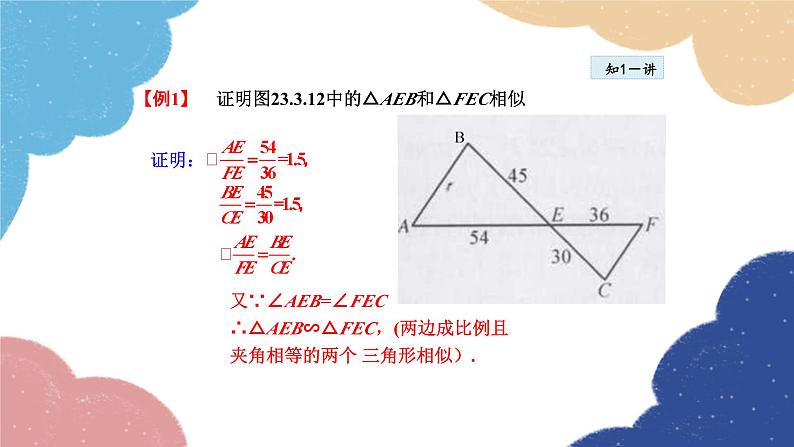
【例1】 证明图中的△AEB和△FEC相似
又∵∠AEB=∠FEC∴△AEB∽△FEC，(两边成比例且夹角相等的两个 三角形相似）.
已知△ABC如图所示，则与△ABC相似的是(　　)
能判定△ABC和△A′B′C′相似的条件是(　　)
相似三角形的判定定理2的应用
【例2】 如图，在正方形ABCD中，P是BC上的点，且BP ＝3PC，Q是CD的中点． 求证：△ADQ∽△QCP.导引： 要证△ADQ与△QCP相似， 已知这两个三角形分别有一 个角为直角，只需证明夹这 对直角的两组对应边成比例 即可．
证明：设正方形ABCD的边长为4a，则AD＝CD＝BC ＝4a， ∵Q是CD的中点，BP＝3PC， ∴DQ＝CQ＝ CD＝2a，PC＝a. 又∵∠D＝∠C＝90°， ∴△ADQ∽△QCP.
利用两边成比例且夹角相等证两三角形相似的方法：首先找出两个三角形中相等的那个角，再分别找出两个三角形中夹这个角的两条边，并按大小排列找出对应边，最后看这两组对应边是否成比例，若成比例则两个三角形相似，否则不相似．
如图，已知 AD＝3 cm，AC＝6 cm，BC＝ 8 cm，则DE的长为________cm.
2 如图，M，N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞，工程人员计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM，AN上，现测得AM＝1千米，AN＝1.8千米，AB＝54米，BC＝45米，AC＝30米，求M，N两点之间的直线距离．