甘肃省武威市凉州区武威第七中学2023-2024学年七年级上学期期末数学试题(含解析)

这是一份甘肃省武威市凉州区武威第七中学2023-2024学年七年级上学期期末数学试题(含解析)，共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
（满分120分，考试时间：120分钟）
一、单选题（每题3分，共计30分）
1．若a与5互为相反数，则a的值为（ ）
A．5B．C．D．
2．方程的解是（ ）
A．B．C．D．
3．中国空间站“天宫一号”运行在距离地球平均高度约375000米处，数375000用科学记数法表示是（ ）
A．B．C．D．
4．已知等式，则下列式子中不成立的是（ ）
A．B．C．D．
5．下列运算正确的是（ ）
A．
B．
C．
D．
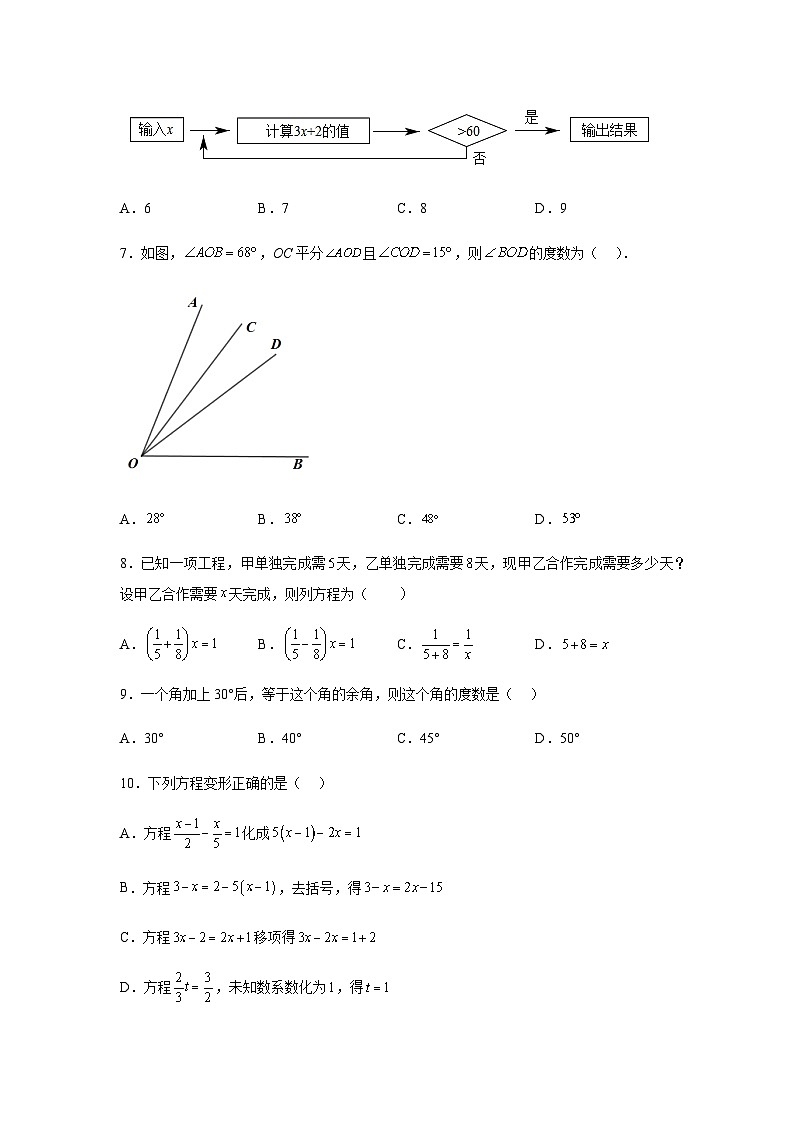
6．如图，按照程序图计算，当输入正整数x时，输出的结果是，则输入的的值可能是（ ）
A．6B．7C．8D．9
7．如图，，OC平分且，则的度数为（ ）．
A．B．C．D．
8．已知一项工程，甲单独完成需天，乙单独完成需要天，现甲乙合作完成需要多少天？设甲乙合作需要天完成，则列方程为（ ）
A．B．C．D．
9．一个角加上30°后，等于这个角的余角，则这个角的度数是（ ）
A．30°B．40°C．45°D．50°
10．下列方程变形正确的是（ ）
A．方程化成
B．方程，去括号，得
C．方程移项得
D．方程，未知数系数化为，得
二、填空题（每题3分，共计24分）
11．的倒数是 ．
12．已知代数式，则 ．
13．按规律填出线上的式子：–2，4x，–8x2，16x3， ．
14．如图，从景点A到景点B有两条路径，游客为了缩短旅途距离而选择路径①，这依据的数学原理是 ．

15．规定：，若，则 ．
16．已知，则的余角度数是 ．
17．线段AB=6，点C在直线AB上，BC=4，则AC的长度为 ．
18．某初中学校七年级举行“数学知识应用能力竞技”活动，测试卷由20道题组成，答对一题得5分，不答或答错一题扣1分，某考生的成绩为70分，则他答对了 道题．
三、解答题（共计66分）
19．计算题
(1)
(2)
(3)
(4)
20．解方程：
(1)；
(2)；
(3)；
(4)．
21．在手工制作课上，老师组织七年级（2）班的学生用硬纸制作圆柱形茶叶筒．七年级（2）班共有学生44人，其中男生人数比女生人数少2人，并且每名学生每小时剪筒身50个或剪筒底120个．
（1）七年级（2）班有男生、女生各多少人？
（2）要求一个筒身配两个筒底，为了使每小时剪出的筒身与筒底刚好配套，应该分配多少名学生剪筒身，多少名学生剪筒底？
22．已知A、B、C、D四点，根据下列要求画图：
（1）画射线AD；
（2）画直线AB；
（3）连接AC、BD交于点O．
23．如图，、是线段上的两点，若，，且是的中点，求的长．
24．如图，O为直线上一点，，平分，且．
(1)求的度数；
(2)试判断是否平分，并说明理由．
25．某校校长暑假将带领该校市级“三好学生”去北京旅游．甲旅行社说：“如果校长买全票一张，则其余学生可享受半价优惠．”乙旅行社说：“包括校长在内，全部按全票价的六折优惠”，两家旅行社的全票价都是240元．
(1)设学生数为x，分别表示两家旅行社的收费；
(2)当学生数是多少时，两家旅行社的收费一样？
(3)就学生数讨论哪家旅行社更优惠．
26．（1）观察一列数，，，，，，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是 ；根据此规律，如果（为正整数）表示这个数列的第n项，那么 ， ．
（2）观察下列等式
，，
将以上三个等式两边相加得
根据上述方法计算：
参考答案与解析
1．B
【分析】根据一个数的相反数就是在这个数前面添上“”号，求解即可．
【详解】解：若a与5互为相反数，
则a的值是，
故选：B．
【点睛】本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．不要把相反数的意义与倒数的意义混淆．
2．C
【分析】方程移项合并，把系数化为1，即可求出解．
【详解】解：方程，
移项得：，
合并得：，
系数化为得：．
故选：C．
【点睛】此题考查了解一元一次方程，熟练掌握方程的解法是解本题的关键．
3．C
【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【详解】解：．
故选：C．
【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．
4．D
【分析】根据等式的性质，逐一判定即可．
【详解】解：A，等式的两边同时减1，等式仍成立，因此成立，故A选项不合题意；
B，等式的两边同时除以3，等式仍成立，因此成立，故B选项不合题意；
C，等式的两边同时乘以3，等式仍成立，因此成立，故C选项不合题意；
D，等式左边减1，右边加1，等式不成立，即不成立，故D选项符合题意；
故选D．
【点睛】本题考查等式的性质，解题的关键是掌握：等式的两边同时加或减同一个式子，等式仍成立；等式的两边同时乘同一个式子，等式仍成立；等式的两边同时除同一个式子(不为零)，等式仍成立．
5．D
【分析】根据合并同类项原理进行判断即可.
【详解】A项,3a+2a=5a,故A项错误.
B项, 3a+3b= 3(a+b), 故B项错误.
C项, ,与幂指数不同, 不能简单合并, 故C项错误.
D项, ,故D项正确.
故本题正确答案为D.
【点睛】本题主要考查求代数式的值，根据合并同类项原理, 底数相同且相同底数对应幂指数相同的项才能合并.
6．A
【分析】分别计算出直接输出结果、两次才输出结果的x的值即可解答．
【详解】解：如果直接输出结果，则，解得：；
如果两次才输出结果：则，解得：；
故选：A．
【点睛】本题主要考查代数式求值、一元一次方程等知识点，掌握逆向思维是解本题的关键．
7．B
【分析】根据OC平分且可得，再结合即可求得答案．
【详解】解：∵OC平分且，
∴，
又∵，
∴，
故选：B．
【点睛】本题考查了角的计算，熟练掌握角平分线的定义是解决本题的关键．
8．A
【分析】利用合作的工作效率等于工作效率的和列出方程求解.
【详解】∵甲单独完成需5天,乙单独完成需要8天,
∴合作的工作效率为:,
设合作x天完成,
∴方程为:,
故选A.
【点睛】本题考查了由实际问题抽象出一元一次方程,重点考查工作时间、工作效率、工作总量三者之间的数量关系,解答时往往把工作总量看做1,再利用它们的数量关系解答.
9．A
【分析】利用题中的“一个角+30°=这个角的余角”作为相等关系列方程求解．
【详解】解：设这个角的度数是x，则
x+30°＝90°﹣x，
解得x＝30°．
答：这个角的度数是30°．
故选：A．
【点睛】此题主要考查了余角的概念以及运用．解此题的关键是熟悉互为余角的两角的和为90°．
10．C
【分析】根据一元一次方程解法，掌握去分母、去括号、移项、合并同类项和系数化为1对各个选项逐项验证即可得到答案．
【详解】解：A、将方程去分母，方程两边同时乘以得到，该选项错误，不符合题意；
B、将方程去括号，根据去括号法则：若括号外是负的，去括号以后括号内各项要变号，得，该选项错误，不符合题意；
C、将方程移项得，该选项正确，符合题意；
D、将方程未知数系数化为，利用等式的性质，方程两边同时乘以，得，该选项错误，不符合题意；
故选：C．
【点睛】本题考查一元一次方程解法步骤，熟练掌握去分母、去括号、移项、合并同类项和系数化为1等方法步骤是解决问题的关键．
11．2021
【分析】根据倒数的含义即可得出答案．
【详解】解：的倒数是2021
故答案为：2021
【点睛】此题主要考查了倒数的定义，乘积为1的两个数互为倒数．
12．4
【分析】根据等式的性质，整体代入即可求解．
【详解】解：∵，
∴，即；
故答案为：4．
【点睛】本题考查了代数式求值，解题关键是根据等式的性质，整体代入求值．
13．-32x4
【分析】根据前四个数发现规律是：第n个数是．
【详解】解：发现规律，第n个数是，那么第5个数是：．
故答案是：．
【点睛】本题考查找规律，解题的关键是能够发现题目中数字之间的规律．
14．两点之间线段最短
【分析】根据两点之间线段最短即可求解．
【详解】根据两点之间线段最短，
故答案为：两点之间线段最短．
【点睛】本题考查线段的定义，掌握两点之间线段最短是解题的关键．
15．
【分析】根据运算规则转化为一元一次方程，然后解即可．
【详解】根据题意可得，
移项，合并同类项得，
系数化为1得，．
故答案为：．
【点睛】本题考查了解一元一次方程的知识，比较新颖，关键是根据题意列出方程．
16．##65度
【分析】根据余角的性质，即可求解．
【详解】解：∵，
∴的余角的度数是．
故答案为：．
【点睛】本题主要考查了余角的性质，熟练掌握互余的两个角的和等于是解题的关键．
17．2或10##10或2
【详解】解：点C在线段AB上，有AC=6-4=2，
点C在AB右侧，AC=4+6=10．
故答案为2或10．
18．15
【分析】根据题意表示出答对以及不答或答错的题目数，进而表示出得分，列方程求解即可得到答案．
【详解】解:设他答对了x道题，则不答或答错了道题，
根据题意可得，，
解得，，
即他答对了15道题．
故答案为：15
【点睛】本题主要考查了一元一次方程的应用，根据题意得出正确的等量关系是解题的关键．
19．(1)
(2)
(3)
(4)
【分析】有理数的混合运算，按照运算法则计算即可．
【详解】（1）解：
（2）解：
（3）解：
（4）解：
【点睛】本题考查了有理数的混合运算，正确的计算是解题的关键．
20．(1)
(2)
(3)
(4)
【分析】本题考查解一元一次方程：
（1）移项、合并同类项，系数化为1即可；
（2）去括号、移项、合并同类项，系数化为1即可；
（3）去括号、移项、合并同类项，系数化为1即可；
（4）去分母、去括号、移项、合并同类项，系数化为1即可．
【详解】（1）解：，
移项，得：，
合并同类项，得：，
系数化为1，得：；
（2）解：
去括号，得：，
移项，得，
合并同类项，得：，
系数化为1，得：；
（3）解：
去括号，得，
移项，得，
合并同类项，得，
系数化为1，得；
（4）解：，
去分母得：，
去括号得：，
移项得：，
合并同类项得：，
系数化为1，得：．
21．解：（1）男生21人，女生23人；（2）24名学生剪筒身，20名学生剪筒底．
【分析】（1）设七年级（2）班有男生x人，根据“共有学生44人，男生人数比女生人数少2人”即可列方程求得结果；
（2）设分配剪筒身的学生为y人，根据“一个筒身配两个筒底，每小时剪出的筒身与筒底刚好配套”即可列方程求得结果．
【详解】（1）设七年级（2）班有男生x人，依题意得
，
解得，
所以，七年级（2）班有男生21人，女生23人；
（2）设分配剪筒身的学生为y人，依题意得
，
解得，，
所以，应该分配24名学生剪筒身，20名学生剪筒底．
【点睛】解题的关键是读懂题意，找到量与量的关系，正确列出一元一次方程，再求解．
22．（1）见解析；（2）见解析；（3）见解析．
【分析】（1）作射线，为端点；
（2）作直线，没有端点；
（3）作线段AC、BD交于点O．
【详解】（1）如图，作射线，为端点；
（2）如图，作直线；
（3）作线段AC、BD交于点O．
【点睛】本题考查了直线，射线，线段的作图，根据有无端点来判断是解题的关键．直线：过两点有且只有一条直线（两点确定一条直线），无端点；射线：直线上的一点，可向一方无限延伸， 有一个端点；线段：直线上两点间的一段，有两个端点．
23．AB=10cm
【分析】根据，可求出的长，再根据是的中点可得出的长，再根据即可求出答案．
【详解】解：∵，，
∴，
又∵是的中点，
∴，
∴．
【点睛】本题考查了两点间的距离，解题的关键是要注意线段的中点等问题的应用．
24．(1)
(2)平分，见解析；
【分析】（1）根据角平分线的定义以及平角的性质进行解答即可；
（2）分别求出和的度数，即可得出结论．
【详解】（1）解：∵，平分，
∴，
∴，
答：的度数为；
（2）∵，，
∴，
∴，
∴，
∴，
∴平分．
【点睛】本题考查了角平分线的定义，角度计算，读懂题意，熟练掌握相关定义是解本题的关键．
25．(1)甲旅行社的收费为240+120x，乙旅行社的收费为144x+144．
(2)当学生数是4人时，两家旅行社的收费一样．
(3)学生数少于4人乙优惠，学生数多于4人甲优惠．
【分析】甲旅行社的收费=240＋学生人数×120，乙旅行社的收费=校长1人＋学生人数×240×0.6．
由甲旅行社的收费=乙旅行社的收费得到方程，求解即可．
由甲旅行社的收费＞乙旅行社的收费得到不等式，求解即可．
【详解】（1）解，即
（2）解：由，得，解得
即当学生数是4人时，两家旅行社的收费一样．
（3）由，得，解得
故：学生数少于4人乙优惠，学生数多于4人甲优惠．
【点睛】本题考查了一元一次方程的实际应用问题，解题的关键是理解题意，根据题意找到等量关系求一元一次方程，然后根据一元一次方程的定义求解．
26．（1）；；；（2）
【分析】（1）根据各数据得到第二项开始，每一项与前一项之比是，则可得到第项所对应的代数式；
（2）根据数字的变化将原式裂项相消计算出结果即可．
【详解】解：（1）根据所给的数据可得：从第二项开始，每一项与前一项之比是一个常数，这个常数是，
则：，
，
，
，
∴，；
故答案为：；；；
（2）解：由题知，
，
故答案为：．
【点睛】本题考查数字的变化规律，解题的关键：（1）通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况并进行应用；（2）根据数字的变化将原式裂项相消．也考查了列代数式和有理数的混合运算．