初中数学华东师大版（2024）九年级上册1. 成比例线段免费练习题

这是一份初中数学华东师大版（2024）九年级上册1. 成比例线段免费练习题，共12页。试卷主要包含了5分钟，5，b=2，c=3，则d=等内容，欢迎下载使用。

附答案：
作业涉及教科书版本：华东师大版 年级及册次：九年级上册
作业涉及单元、章节（或主题、任务）：23.1.成比例线段
作业设计教师姓名：仁寿县富加镇玉龙初级中学校 袁宇平
单元、章节（或主题、任务）整体性作业设计思路说明：
成比例线段是初三上学期几何部分的教学内容之一，在课程标准中图形的变化之图形的相似有相关的内容要求是：了解比例的基本性质、线段的比、成比例的线段；通过建筑、艺术上的实例了解黄金分割。华东师大版的教材上针对这一内容，设计了二课时的教学任务,第一课时成比例线段，第二课时平行线分线段成比例，理解并掌握其定理及推论，学会运用。小学5—6年级阶段的数量关系中也有对比和比例的内容要求和学业要求，要求在实际情境中理解比和比例以及按比例分配的含义，能解决简单的问题；会判断两个量的比，会计算比值。本节的学习，可承上启下，旨在复习小学时学习的比和比例并为进一步学好相似三角形做准备。为了帮助学生更好地理解和掌握这部分内容，设计了如下相关作业：
1、课前作业在基础性作业中设计选择填空，旨在检测学生预习成比例线段和平行线分线段成比例的相关知识。知道四条线段中，有两条线段长度的比等于另两条线段长度的比，则这四条线段成比例，理解平行线分线段成比例定理及推论，并能解决相关简单的数学问题；在发展性作业设计中，也有类似的题型，巩固运用，从而培养学生的思维和计算能力。
2、课中作业：在讲新课后，设计的作业分为基础性和发展性，主要是选择题和解答题，让学生会快速判断四条线段成比例，运用比例的等比、合比性质解决相关问题。同时注重训练学生思维能力和规范书写的能力。从而培养学生爱数学、用数学的情感。
3、课后作业：共设计三个题，巩固所学知识和注重培养个性发展，在训练书写的同时渗透数形结合思想。
第1课时 成比例线段
使用时段
作业内容
作业设计
设计意图
使用者
预计时长
预估难度系数
课前
基础性作业
作业一
下列a、b、c、d四条线段成比例的是（ ）.
A、a=1cm b=2cm c=3cm d=4cm
B、a=3cm b=4cm c=5cm d=6cm
C、a=2cm b=3cm c=4cm d=5cm
D、a=4cm b=3cm c=2cm d=6cm
2. 在比例式ab = cd 中，比例外项是 ，比例内项是 .
初步判断成比例线段
学生
0.5分钟
0.9
线段a、b、c满足关系式ab = b c ，且b=6，则ac=
比例中，两内项的积等于两外项的积
学生
0.5分钟
0.8
4. 已知mn = 12 ，则m+nn = , m−nn = .
利用合比解决相关题型
学生
1分钟
0.8
发展性作业
作业一
已知四条线段a、b、c、d成比例，且a=1.5，b=2，c=3，则d=
如果数b是a、c的比例中项，a=5，c=15，那么b=
运用比例的相关知识解决问题
学生
2分钟
0.8
课中
基础性作业
作业一
1.a、b、c、d四条线段成比例的是（ ）
A、a=1.5cm b=2.5cm c=3.5cm d=4.5cm
B、a=1cm b=2 cm c=2cm d=2cm
C、a=1cm b=3cm c=2cm d=5 cm
D、a=2cm b=3 cm c=5 cm d=1cm
2.判断下列四条线段是否是成比例线段
（1）3，6，9，2
（2）4，7，8，3
会判断四条线段成比例
学生
1-2分钟
0.6
作业二
1.已知4a−3b2a−b = 34，求ba的值.
2.已知a4 = b5 = c6 ,求3a−2b+4ca+4b的值
3.已知a−bb =47，则ab=

培养学生计算能力
学生
3分钟左右
0.6
发展性作业
作业一
如果线段c是b、d的比例中项，b:d=4:9，那么下列说法正确的是（ ）
b:c=4：9 B、c:d=2:3
C、 b:c=2:2 D、c:d=3:2
利用比例各项的关系解题。
学生
1分钟左右
0.5
作业二
已知a b = cd，求证：
（1）a+bb = c+dd
（2） aa−b = cc−d
（3） ab = cd = a+cb+d (b+d≠0)
注重学生思维能力的培养和良好书写习惯的训练。
学生
4分钟左右
0.7
课后
基础性作业
作业一
写出四条线段成比例
发散思维，个性培养
学生
1分钟
0.8
发展性作业
已知a、b、c是△ABC的三边，且满足a+43 = b+32 = c+84 ，a+b+c=12.
试求a、b、c的值
判断△ABC的形状
书写能力训练
学生
2分钟左右
0.5
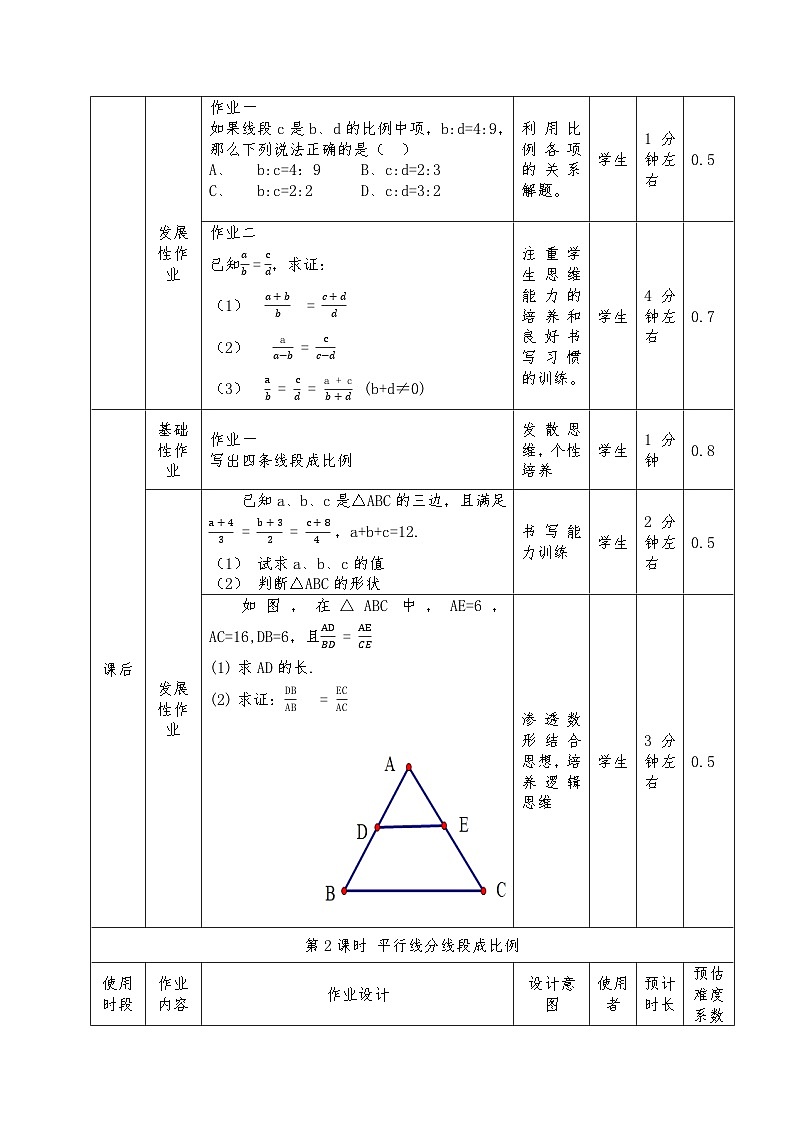
如图，在△ABC中，AE=6，AC=16,DB=6，且ADBD = AECE
求AD的长.
求证：DBAB = ECAC

渗透数形结合思想，培养逻辑思维
学生
3分钟左右
0.5
第2课时 平行线分线段成比例
使用时段
作业内容
作业设计
设计意图
使用者
预计时长
预估难度系数
课前
基础性作业
作业一
1、下列a、b、c、d四条线段成比例的是（ ）.
A、a=2.1cm b=2cm c=3.1cm d=3cm
B、a=3.5cm b=4cm c=5.5cm d=6cm
C、a=2cm b=3cm c=4cm d=5cm
D、a=4cm b=3cm c=2cm d=6cm

初步判断成比例线段
学生
0.5分钟
0.9
线段a、b、c满足关系式ab = b c ，且b=7，则ac=
比例中，两内项的积等于两外项的积
学生
0.5分钟
0.8
3、 已知mn = 23 ，则m+nn = , m−nn = .
利用合比解决相关题型
学生
1分钟
0.8
发展性作业
作业一
已知四条线段a、b、c、d成比例，且a=1.5，b=3，c=3，则d=
如果数b是a、c的比例中项，a=6，c=15，那么b=
运用比例的相关知识解决问题
学生
2分钟
0.8
课中
基础性作业
作业一
如图，直线l1‖l2‖l3,分别截直线m、n于点A、B、C和点D、E、F，且AB=6,DE=8,EF=4,则：
BC:AB=
AB:AC=
（3） BC*DE=
（4） BC*EF=

2.如图，AB‖CD‖EF，则下列结论正确的是（）
A.CE/CB=DF/DA B.AD/DF=CE/BC
C.BC/BE=AD/DF D.CE/BE=AF/AD

3.如图，E是▭ABCD的边AD上一点，CE交BA的延长线于点F,若AE/DE=2/3,AB=4,求AF的长。

会判断四条线段成比例，初步感知平行线分线段成比例的对应方式
学生
4分钟左右
0.7
作业二
1如图，D是△ABC的边BC上的点,CD：BD=1:3,E是AD的中点，连结BE并延长，交AC于点F,求BE:EF的值。

培养学生逻辑思维能力
学生
3分钟左右
0.6
发展性作业
作业一
1、如图，在△ABC中，点D、E在边AB上，点F在边AC上，DF‖BC,EF‖CD,AF=3,AD=4,AE=2.
求CF的长.
求AB的长.

利用平行线分线段成比例解题。
学生
3分钟左右
0.5
2、如图，在△ABC中，点D、E分别在边AB、AC上，DE‖BC,BD=AE.若AB=8，AC=6,则AE=
注重学生思维能力的培养
学生
1分钟左右
0.7
课后
基础性作业
作业一
如图，直线a‖b‖c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB/BC=1/2.则DE/DF=
巩固平行线分线段成比例的对应关系
学生
1分钟
0.8
发展性作业
如图，在△ABC中，AD是边BC上的中线，点F在AD上，且AF：DF=1：2，连结BF并延长交边AC于点E，求AE/CE的值。


书写能力训练
培养逻辑思维
学生
4分钟左右
0.5
第1课时 成比例线段
使用时段
作业内容
作业设计
课前
基础性作业
作业一
下列a、b、c、d四条线段成比例的是（ D ）.
A、a=1cm b=2cm c=3cm d=4cm
B、a=3cm b=4cm c=5cm d=6cm
C、a=2cm b=3cm c=4cm d=5cm
D、a=4cm b=3cm c=2cm d=6cm
2. 在比例式ab = cd 中，比例外项是 a、d ，比例内项是 b、c .
线段a、b、c满足关系式ab = b c ，且b=6，则ac= 36
4. 已知mn = 12 ，则m+nn = 32 , m−nn = -12 .
发展性作业
作业一
已知四条线段a、b、c、d成比例，且a=1.5，b=2，c=3，则d= 4
如果数b是a、c的比例中项，a=5，c=15，那么b= 53
课中
基础性作业
作业一
1.a、b、c、d四条线段成比例的是（B ）
A、a=1.5cm b=2.5cm c=3.5cm d=4.5cm
B、a=1cm b=2 cm c=2cm d=2cm
C、a=1cm b=3cm c=2cm d=5 cm
D、a=2cm b=3 cm c=5 cm d=1cm
2.判断下列四条线段是否是成比例线段
（1）3，6，9，2 不成比例线段
（2）4，7，8，3 不成比例线段
作业二
已知4a−3b2a−b = 34，求ba的值.
解：∵ 4a−3b2a−b = 34
∴4（4a-3b）=3（2a-b）
∴ 10a=9b
∴ba = 109
已知a4 = b5 = c6 ,求3a−2b+4ca+4b的值
解：设 a4 = b5 = c6 =m
∴a=4m,b=5m,c=6m
∴ 3a−2b+4ca+4b =3∗4m−2∗5m+4∗6m4m+4∗5m
= 12m−10m+24m4m+20m = 26m24m = 1312
3.已知a−bb =47，则 ab = 117

发展性作业
作业一
如果线段c是b、d的比例中项，b:d=4:9，那么下列说法正确的是（B ）
b:c=4：9 B、c:d=2:3
C、 b:c=2:2 D、c:d=3:2
作业二
已知a b = cd，求证：
a+bb = c+dd
证明：∵ a b = cd
∴a b +1 = cd +1
∴a+bb = c+dd
aa−b = cc−d
证明：∵ a b = cd ∴ba = dc ∴ba = dc
∴- ba = - dc ∴1- ba = 1- dc ∴a−ba=c−dc
∴aa−b= cc−d
（3） ab = cd = a+cb+d (b+d≠0)
证明：∵a b = cd ∴ac = bd ∴ac+1 = bd +1
∴a+cc = b+dd ∴a+cb+d = cd
∴ab = cd = a+cb+d (b+d≠0)
课后
基础性作业
作业一
写出四条线段成比例
发展性作业
1、已知a、b、c是△ABC的三边，且满足a+43 = b+32 = c+84 ，a+b+c=12.
试求a、b、c的值 a=5 b=3 c=4
判断△ABC的形状 直角三角形
如图，在△ABC中，AE=6，AC=16,DB=6，且ADBD = AECE
求AD的长. AD=3.6
求证：DBAB = EAAC

第2课时 平行线分线段成比例
使用时段
作业内容
作业设计
课前
基础性作业
作业一
1、下列a、b、c、d四条线段成比例的是（ D ）.
A、a=2.1cm b=2cm c=3.1cm d=3cm
B、a=3.5cm b=4cm c=5.5cm d=6cm
C、a=2cm b=3cm c=4cm d=5cm
D、a=4cm b=3cm c=2cm d=6cm

线段a、b、c满足关系式ab = b c ，且b=7，则ac= 49
3、 已知mn = 23 ，则m+nn = 53 ,
m−nn = - 13 .
发展性作业
作业一
已知四条线段a、b、c、d成比例，且a=1.5，b=3，c=3，则d= 6
如果数b是a、c的比例中项，a=6，c=15，那么b= 310
课中
基础性作业
作业一
如图，直线l1‖l2‖l3,分别截直线m、n于点A、B、C和点D、E、F，且AB=6,DE=8,EF=4,则：
BC:AB= 1:2
AB:AC= 2:3
（3） BC*DE= 24
（4） BC*EF= 12

2.如图，AB‖CD‖EF，则下列结论正确的是（A）
A.CE/CB=DF/DA B.AD/DF=CE/BC
C.BC/BE=AD/DF D.CE/BE=AF/AD

3.如图，E是▭ABCD的边AD上一点，CE交BA的延长线于点F,若AE/DE=2/3,AB=4,求AF的长。AF= 83

作业二
1如图，D是△ABC的边BC上的点,CD：BD=1:3,E是AD的中点，连结BE并延长，交AC于点F,求BE:EF的值。BEFE =7

发展性作业
作业一
1、如图，在△ABC中，点D、E在边AB上，点F在边AC上，DF‖BC,EF‖CD,AF=3,AD=4,AE=2.
(1)求CF的长.CF=3
(2)求AB的长. AB=8

2、如图，在△ABC中，点D、E分别在边AB、AC上，DE‖BC,BD=AE.若AB=8，AC=6,则AE= 247
课后
基础性作业
作业一
如图，直线a‖b‖c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB/BC=1/2.则DE/DF= 13
发展性作业
如图，在△ABC中，AD是边BC上的中线，点F在AD上，且AF：DF=1：2，连结BF并延长交边AC于点E，求AE/CE的值。
AECE=14