
小学数学北师大版(2024)五年级上册2 探索活动:成长的脚印当堂检测题
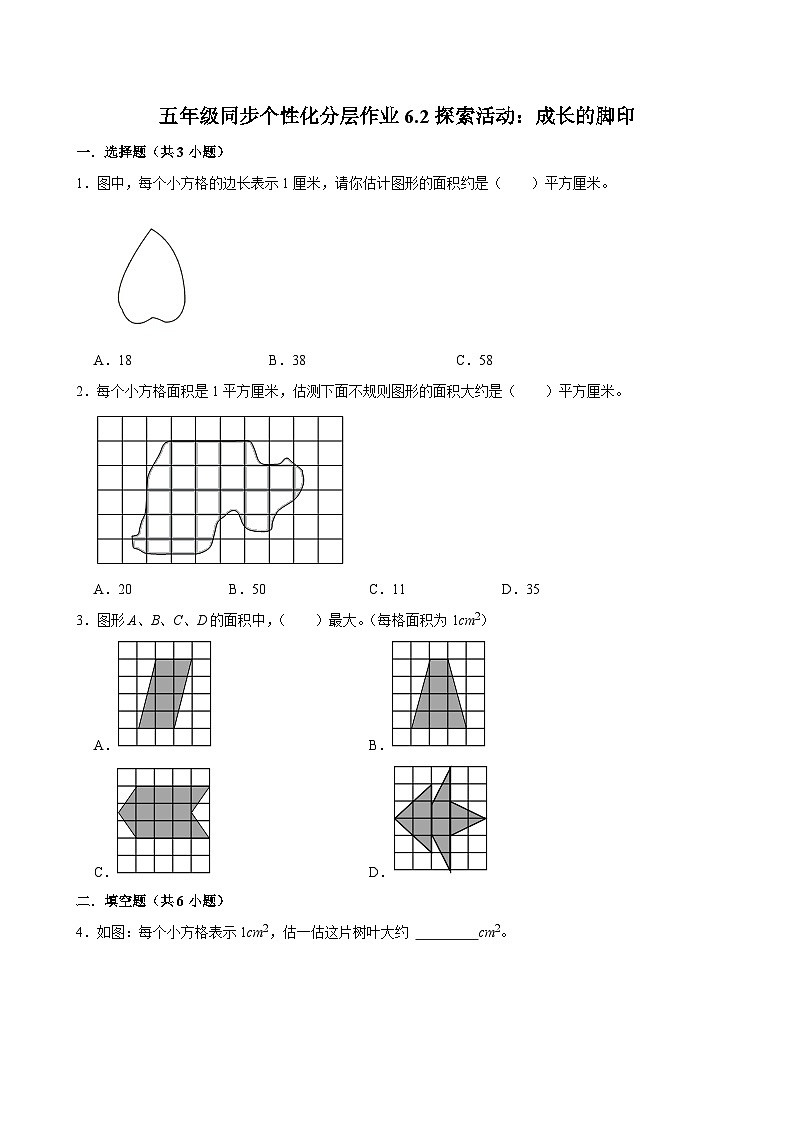
展开1.图中,每个小方格的边长表示1厘米,请你估计图形的面积约是( )平方厘米。
A.18B.38C.58
2.每个小方格面积是1平方厘米,估测下面不规则图形的面积大约是( )平方厘米。
A.20B.50C.11D.35
3.图形A、B、C、D的面积中,( )最大。(每格面积为1cm2)
A.B.
C.D.
二.填空题(共6小题)
4.如图:每个小方格表示1cm2,估一估这片树叶大约 cm2。
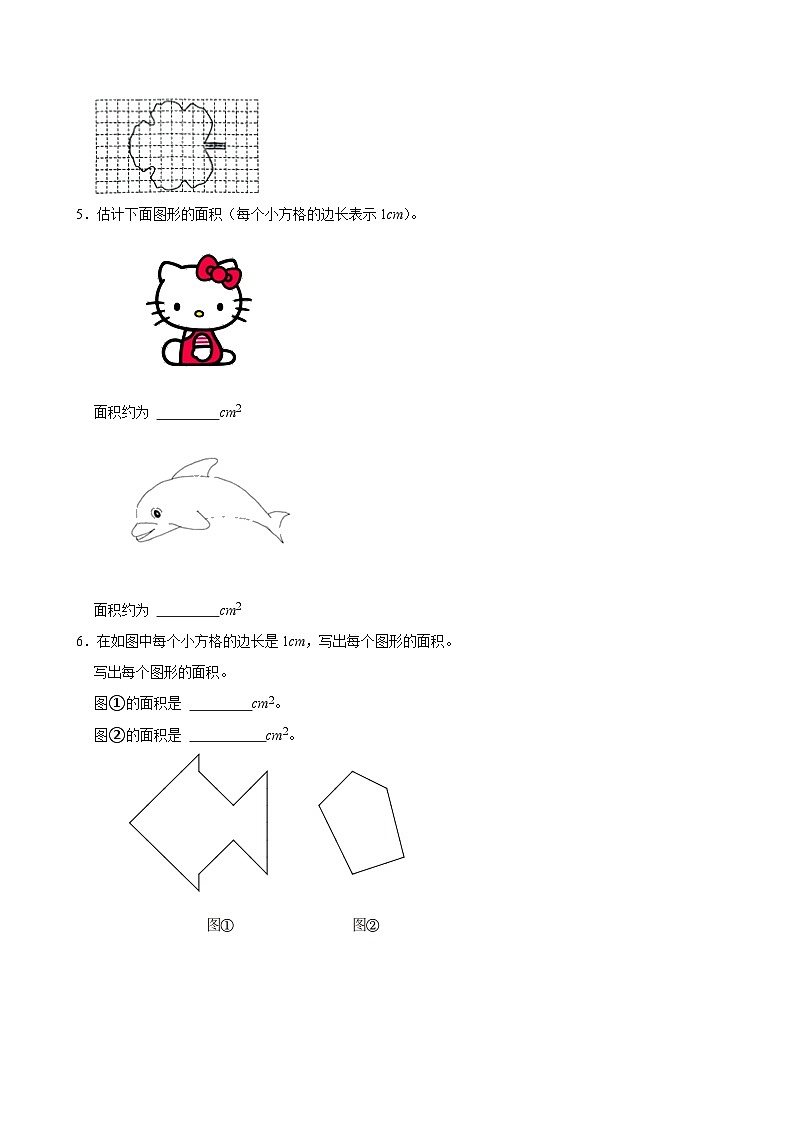
5.估计下面图形的面积(每个小方格的边长表示1cm)。
面积约为 cm2
面积约为 cm2
6.在如图中每个小方格的边长是1cm,写出每个图形的面积。
写出每个图形的面积。
图①的面积是 cm2。
图②的面积是 cm2。
7.
估一估图A的面积是 ;图B被撕去了一部分,原来正方形的面积至少是 (每个小方格的面积为1平方厘米);图C中涂色部分的面积是 。
8.估计图中每个图形的面积。(每格表示1cm2)
(1)左图的面积大约是 cm2;
(2)右图的面积大约是 cm2。
9.如图的每个小方格表示1cm2,估计树叶的面积:
(1)用图1的方法估计,面积约 cm2。
(2)在原图画一画,转化成其它的基本图形或组合图形来估计,面积约 cm2。
三.解答题(共1小题)
10.找几种生活中的物品,先估一估表面周长,再算一算,填在表里.
五年级同步个性化分层作业6.2探索活动:成长的脚印
参考答案与试题解析
一.选择题(共3小题)
1.图中,每个小方格的边长表示1厘米,请你估计图形的面积约是( )平方厘米。
A.18B.38C.58
【考点】估测.
【专题】几何直观.
【答案】B
【分析】根据利用数方格的方法计算图形的面积,先数整格,再数不满一格的,不满一格的按照半格来数,据此解答。
【解答】解:28+18÷2
=29+9
=38(平方厘米)
答:图形的面积约是38平方厘米。
故选:B。
【点评】这道题目考查的是用数方格的方法来估测图形的面积。
2.每个小方格面积是1平方厘米,估测下面不规则图形的面积大约是( )平方厘米。
A.20B.50C.11D.35
【考点】用方格纸计算图形面积.
【专题】几何直观;运算能力.
【答案】A
【分析】每个小方格的面积为1平方厘米。图片中不满一格或者不满半格的小方格都按照半格计算,数出有不规则图形所占的小方格,即可得出答案。
【解答】解:数出来不满一格和不满半格的小方格有17个,满格的小方格有14个。
所以不规则图形的面积为:
17÷2+14
=8.5+14
=22.5(平方厘米)
22.5≈20
故选:A。
【点评】本题考查学生对用方格纸计算不规则图形的掌握和运用。
3.图形A、B、C、D的面积中,( )最大。(每格面积为1cm2)
A.B.
C.D.
【考点】用方格纸计算图形面积.
【专题】平面图形的认识与计算;几何直观.
【答案】C
【分析】用数格子的方法对阴影部分的面积进行估算,先数整格数,再数半格,两个半格算一格,据此解答。
【解答】解:图一:2×4=8(平方厘米)
图二:(3+1)×4÷2
=4×4÷2
=8(平方厘米)
图三:3×4=12(平方厘米)
图四:10平方厘米。
因为12>10>8,因此图三面积最大。
故选:C。
【点评】本题考查了利用数格子计算不规则物体的面积。
二.填空题(共6小题)
4.如图:每个小方格表示1cm2,估一估这片树叶大约 42 cm2。
【考点】估测.
【专题】几何直观.
【答案】42。
【分析】利用数格子的方法解答,先数整格数,不满一格的按2个半格算一格,据此解答。
【解答】解:31+22÷2
=31+11
=42(平方厘米)
估一估这片树叶大约42cm2。
故答案为:42。
【点评】本题考查了计算不规则物体面积的求法。
5.估计下面图形的面积(每个小方格的边长表示1cm)。
面积约为 15 cm2
面积约为 14 cm2
【考点】估测.
【专题】几何直观.
【答案】15,14。(答案不唯一)
【分析】根据利用方格图计算图形面积的方法,不满格的按半格计算,据此解答即可。
【解答】解:
满格的是7格,半格的是16个,所以它的面积是7+16×0.5=15(平方厘米);
面积约为15cm2
满格的是7格,半格的是14个,所以它的面积是7+14×0.5=14(平方厘米)
面积约为14cm2
故答案为:15,14。(答案不唯一)
【点评】此题考查的目的是理解掌握利用方格图计算图形面积的方法及应用,不满格的按半格计算。
6.在如图中每个小方格的边长是1cm,写出每个图形的面积。
写出每个图形的面积。
图①的面积是 32 cm2。
图②的面积是 18.5 cm2。
【考点】用方格纸计算图形面积.
【专题】几何直观.
【答案】32,18.5。
【分析】首先把图形用方格划分,注意每一部分估算取整,最后合并即可得出答案。
【解答】解:24+8=32(cm2)
答:图①的面积是32cm2。
11+15÷2
=11+7.5
=18.5(cm2)
答:图②的面积是18.5cm2。
故答案为:32,18.5。
【点评】解决此题的关键是利用割补法,把不规则的图形拼为规则的图形,进一步估算面积即可。
7.
估一估图A的面积是 6平方分米 ;图B被撕去了一部分,原来正方形的面积至少是 16平方厘米 (每个小方格的面积为1平方厘米);图C中涂色部分的面积是 10平方米 。
【考点】用方格纸计算图形面积;长方形、正方形的面积.
【专题】平面图形的认识与计算;模型思想.
【答案】6平方米,16平方厘米,10平方米。
【分析】图A通过观察可知,长方形的面积大约有6个这样的小正方形的面积,利用小正方形的面积乘6即可;图B原图是一个正方形,正方形的边长是4,因此面积利用边长×边长即可计算原图面积;图C先利用1×1求出一个正方形的面积,再利用数格子的方法数出有几个格,最后利用面积乘格子数即可。
【解答】解:1×6=6(平方分米)
4×4=16(平方厘米)
1×1×10
=1×10
=10(平方米)
答:估一估图A的面积是6平方分米;图B被撕去了一部分,原来正方形的面积至少是16平方厘米;图C中涂色部分的面积是10平方米。
故答案为:6平方分米,16平方厘米,10平方米。
【点评】本题考查了利用数格子、图形的拼接法及推理法求不规则图形的面积。
8.估计图中每个图形的面积。(每格表示1cm2)
(1)左图的面积大约是 57 cm2;
(2)右图的面积大约是 36 cm2。
【考点】用方格纸计算图形面积.
【专题】平面图形的认识与计算;几何直观.
【答案】57,36。
【分析】先数图形占的整格数,再数半格数,两个半格算一个满格,据此计算解答。
【解答】解:(1)46+22÷2
=46+11
=57(平方厘米)
答:左图的面积大约是57cm2。
(2)26+20÷2
=26+10
=36(平方厘米)
答:右图的面积大约是36cm2。
故答案为:57,36。
【点评】本题考查了利用数格子的方法计算不规则物体的面积。
9.如图的每个小方格表示1cm2,估计树叶的面积:
(1)用图1的方法估计,面积约 40 cm2。
(2)在原图画一画,转化成其它的基本图形或组合图形来估计,面积约 40 cm2。
【考点】用方格纸计算图形面积.
【专题】几何直观.
【答案】40;40。
【分析】根据利用数方格计算图形面积的方法,不满格的按半格计算,通过观察图形可知:满格的有28格,不满格的是24格,所以这个图形的面积约是40cm2,再根据长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:(1)满格的有26格,不满格的是28格,所以这个图形的面积是约是26+(28÷2)=40(cm2);
(2)8×5=40(cm2)
答:这个图形的面积是30平方厘米.
故答案为:40;40。
【点评】此题考查的目的是理解掌握可以数方格的方法计算图形的面积,以及长方形面积公式的灵活运用。
三.解答题(共1小题)
10.找几种生活中的物品,先估一估表面周长,再算一算,填在表里.
【考点】估测;长度的测量方法.
【专题】平面图形的认识与计算.
【答案】见试题解答内容
【分析】根据生活实际,先估算出围成各个物品表面图形的所有边的长度,进而相加估算出周长;再用直尺测量出各个图形的所有边的长度,求和即可解答.
【解答】解:
【点评】此题主要考查的是学生估算的能力和实际操作测量的能力.
考点卡片
1.长度的测量方法
【知识点归纳】
1.长度的测量:长度的测量是最基本的测量,最常用的工具是刻度尺.
2.正确使用刻度尺刻度线、量程、分度值.
使用时要注意:
(1)尺子要沿着所测长度放,尺边对齐被测对象,必须放正重合,不能歪斜.
(2)不利用磨损的零刻度线,如因零刻线磨损而取另一整刻度线为零刻线的,切莫忘记最后读数中减掉取代零刻线的刻度值.
(3)厚尺子要垂直放置
(4)读数时,视线应与尺面垂直.
【命题方向】
常考题型:
例:量出每条边的长度,以毫米为单位.
分析:用直尺的“0”刻度线和线段的一个端点重合,另一个端点在直尺上的刻度,就是该线段的长度.
解:测量数据如下图:
点评:本题考查了学生测量线段的能力.
2.长方形、正方形的面积
【知识点归纳】
长方形面积=长×宽,用字母表示:S=ab
正方形面积=边长×边长,用字母表示:S=a2.
【命题方向】
常考题型:
例1:一个长方形的周长是48厘米,长和宽的比是7:5,这个长方形的面积是多少?
分析:由于长方形的周长=(长+宽)×2,所以用48除以2先求出长加宽的和,再根据长和宽的比是7:5,把长看作7份,宽看作5份,长和宽共7+5份,由此求出一份,进而求出长和宽分别是多少,最后根据长方形的面积公式S=ab求出长方形的面积即可.
解:一份是:48÷2÷(7+5),
=24÷12,
=2(厘米),
长是:2×7=14(厘米),
宽是:2×5=10(厘米),
长方形的面积:14×10=140(平方厘米),
点评:本题考查了按比例分配的应用,同时也考查了长方形的周长公式与面积公式的灵活运用.
答:这个长方形的面积是140平方厘米.
例2:小区前面有一块60米边长的正方形空坪,现要在空坪的中间做一个长32米、宽28米的长方形花圃,其余的植上草皮.(如图)
①花圃的面积是多少平方米?
②草皮的面积是多少平方米?
分析:(1)长方形的面积=长×宽,代入数据即可求解;
(2)草皮的面积=正方形的面积﹣长方形的面积,利用正方形和长方形的面积公式即可求解.
解:(1)32×28=896(平方米);
(2)60×60﹣896,
=3600﹣896,
=2704(平方米);
答:花圃的面积是896平方米,草皮的面积是2704平方米.
点评:此题主要考查正方形和长方形的面积的计算方法.
【解题思路点拨】
(1)常规题求正方形面积,先求出边长,代入公式即可求得;求长方形面积,分别求出长和宽,代入公式即可求得,面积公式要记牢.
(2)其他求法可通过分割补,灵活性高.
3.用方格纸计算图形面积
【知识点归纳】
利用方格纸中的格子都是正方形,从而间接求出图形的面积
【命题方向】
常考题型:
1.计算图形的面积。(每个小方格的边长是1厘米)
分析:根据图形的特点,可以利用“割补”法,拼成两个平行四边形,根据平行四边形的面积公式:S=ah,把数据代入公式解答。
解:3×4+3×6
=12+18
=30(平方厘米)
答:这个组合图形的面积是30平方厘米。
2.如图,在正方形网格上有一个△ABC.若网格上的最小正方形的边长为1,求△ABC的面积.
答案:2×3×½=3
4.估测
【知识点归纳】
1.按四舍五入的原则估算成整百数再计算答案;
2.按四舍五入的原则估算成整十数再计算答案.
但注意,一道题目中采取的方法要一致,不能第一个数按整百估算,第二个数按整十数估算.如果先算后估就不叫估算,应称为求近似数.
【命题方向】
常考题型:
例:100本第十二册小学数学课本的厚度接近( )
A、7毫米 B、7厘米 C、7米 D、7分米
分析:根据生活经验,一本数学书的厚度大约是7毫米,那么100本书的厚度大约是7分米.
解:一本数学书的厚度大约是7毫米,那么100本书的厚度大约是7分米.
故选:D.
点评:估算在生产和生活中有着广泛的用途,对于小学生学习数学来说,利用估算可提高分析与解答问题的能力.
物品名称
估计周长
实际周长
物品名称
估计周长
实际周长
物品名称
估计周长
实际周长
数学作业本封面的周长
(30+20)×2=100(厘米)
(31+20)×2=102(厘米)
课桌桌面的周长
(100+50)×2=300(厘米)
(98+45)×2=286(厘米)
一块玻璃的周长
(50+50)×2=200(厘米)
(55+52)×2=214(厘米)
文具盒的表面周长
(20+6)×2=52(厘米)
(22+8)×2=60(厘米)
数学五年级上册2 探索活动:成长的脚印课时训练: 这是一份数学五年级上册<a href="/sx/tb_c100602_t7/?tag_id=28" target="_blank">2 探索活动:成长的脚印课时训练</a>,共14页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。
小学数学北师大版五年级上册2 探索活动:成长的脚印随堂练习题: 这是一份小学数学北师大版五年级上册<a href="/sx/tb_c100602_t7/?tag_id=28" target="_blank">2 探索活动:成长的脚印随堂练习题</a>,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
数学五年级上册2 探索活动:成长的脚印当堂检测题: 这是一份数学五年级上册2 探索活动:成长的脚印当堂检测题,共9页。试卷主要包含了选择题,填空题,判断题,解答题等内容,欢迎下载使用。














