2025届江西省宁都县第二中学数学九年级第一学期开学检测试题【含答案】

这是一份2025届江西省宁都县第二中学数学九年级第一学期开学检测试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如果是任意实数，下列各式中一定有意义的是（ ）
A．B．C．D．
2、（4分）下列因式分解正确的是（ ）
A．x3﹣x＝x（x2﹣1）B．x2+y2＝（x+y）（x﹣y）
C．（a+4）（a﹣4）＝a2﹣16D．m2+4m+4＝（m+2）2
3、（4分）如图，在平行四边形ABCD中，下列结论错误的是（ ）
A．∠BDC＝∠ABDB．∠DAB＝∠DCB
C．AD＝BCD．AC⊥BD
4、（4分）下列各等式成立的是（ ）
A．B．
C．D．
5、（4分）禽流感病毒的形状一般为球形，直径大约为0.000000102m，该直径用科学记数法表示为（ ）
A．1.02×10﹣7mB．10.2×10﹣7mC．1.02×10﹣6mD．1.0×10﹣8m
6、（4分）已知△ABC和△A′B′C′是位似图形．△A′B′C′的面积为6cm2，周长是△ABC的一半．AB＝8cm，则AB边上高等于 （ ）
A．3 cm B．6 cm C．9cm D．12cm
7、（4分）一名老师带领x名学生到动物园参观，已知成人票每张30元，学生票每张10元．设门票的总费用为y元，则y与x的函数关系为（ ）
A．y=10x+30B．y=40xC．y=10+30xD．y=20x
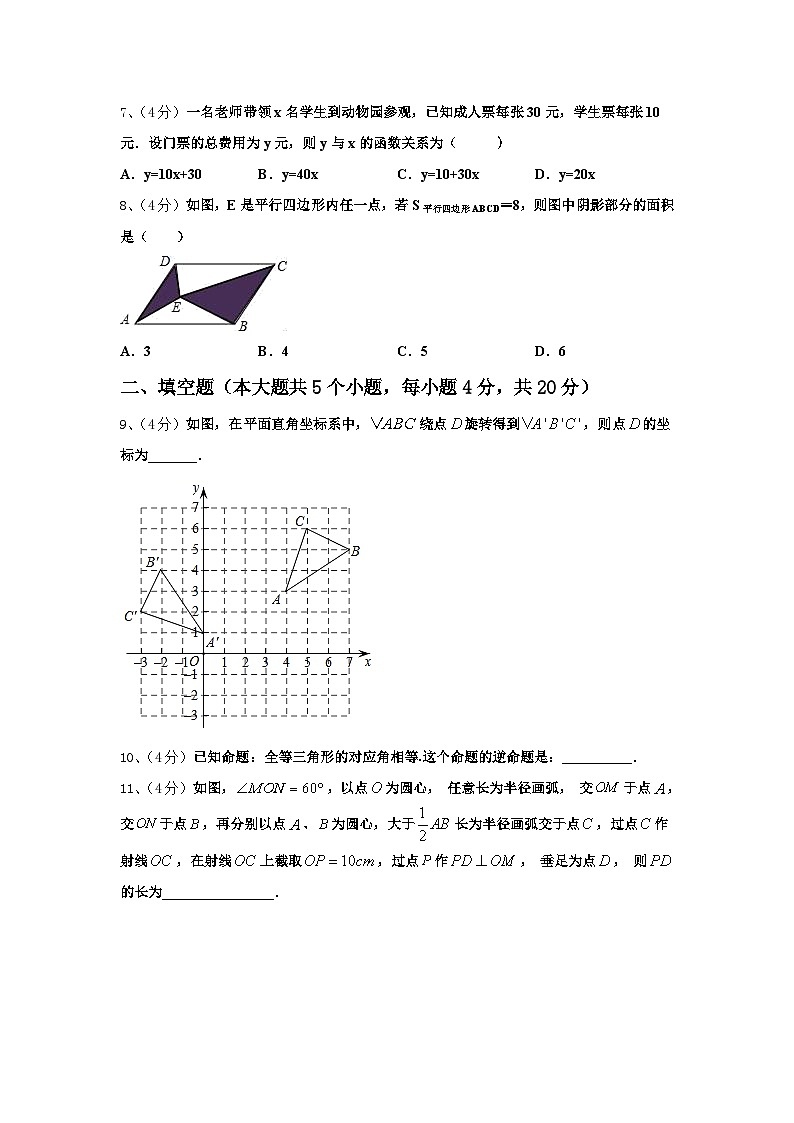
8、（4分）如图，E是平行四边形内任一点，若S平行四边形ABCD＝8，则图中阴影部分的面积是（ ）
A．3B．4C．5D．6
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在平面直角坐标系中，绕点旋转得到，则点的坐标为_______．
10、（4分）已知命题：全等三角形的对应角相等.这个命题的逆命题是：__________．
11、（4分）如图，，以点为圆心， 任意长为半径画弧， 交于点，交于点，再分别以点、为圆心，大于长为半径画弧交于点，过点作射线，在射线上截取，过点作， 垂足为点， 则的长为________________．
12、（4分）将函数y=3x+1的图象沿y轴向下平移2个单位长度，所得直线的函数表达式为_____．
13、（4分）如图，直线y=kx+b（k≠0）与x轴交于点（﹣4，0），则关于x的方程kx+b=0的解为x=_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D,
（1）求证：BE＝CF ；
（2）当四边形ACDE为菱形时，求BD的长．
15、（8分）阅读下列解题过程：
；
.
请回答下列问题：
（1）计算；
（2）计算.
16、（8分）已知：如图，C为线段BE上一点，AB∥DC，AB=EC，BC=CD．
求证：∠A=∠E．
17、（10分）如图，两块大小不等的等腰直角三角形按图1放置，点为直角顶点，点在上，将绕点顺时针旋转角度，连接、.
（1）若，则当 时，四边形是平行四边形；
（2）图2，若于点，延长交于点，求证：是的中点；
（3）图3，若点是的中点，连接并延长交于点，求证：.
18、（10分）如图1，在正方形ABCD中，点E是AB上一点，点F是AD延长线上一点，且DF=BE，连接CE、CF．
（1）求证：CE=CF．
（2）在图1中，若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗；为什么；
（3）根据你所学的知识，运用（1）、（2）解答中积累的经验，完成下列各题，如图2，在四边形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，且∠DCE=45°．
①若AE=6，DE=10，求AB的长；
②若AB=BC=9，BE=3，求DE的长．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）直线y＝3x﹣1向上平移4个单位得到的直线的解析式为：_____．
20、（4分）某公司招聘英语翻译，听、说、写成绩按3∶3∶2计入总成绩.某应聘者的听、说、写成绩分别为80分，90分，95分（单项成绩和总成绩满分均为百分制），则他的总成绩为____________分.
21、（4分）如图，以正方形ABCD的BC边向外作正六边形BEFGHC，则∠ABE＝___________度．
22、（4分）______.
23、（4分）分解因式：m2﹣9m＝_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）计算：
（1）
（2）已知a＝+2，b＝﹣2，求a2﹣b2的值．
25、（10分）有3个完全相同的小球，把它们分别标号为1，2，3，放在一个口袋中，随机地摸出一个小球不放回，再随机地摸出一个小球．
（1）采用树形图法（或列表法）列出两次摸球出现的所有可能结果；
（2）求摸出的两个球号码之和等于5的概率．
26、（12分）小芳从家骑自行车去学校，所需时间()与骑车速度()之间的反比例函数关系如图．
(1)小芳家与学校之间的距离是多少？
(2)写出与的函数表达式；
(3)若小芳点分从家出发，预计到校时间不超过点分，请你用函数的性质说明小芳的骑车速度至少为多少？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据二次根式有意义，二次根式中的被开方数是非负数，分式要有意义分母不为零，进行分析即可．
【详解】
A. 当a<0时，无意义，故此选项错误；
B. 当a>0或a<0时, 无意义，故此选项错误；
C. 当a=0时, 无意义，故此选项错误；
D. a是任意实数, 都有意义，故此选项正确；
故选D.
本题考查二次根式有意义的条件，需注意是a取任何值时二次根式都要有意义，若存在使二次根式无意义的a皆是错.
2、D
【解析】
逐项分解因式，即可作出判断．
【详解】
A、原式＝x（x2﹣1）＝x（x+1）（x﹣1），不符合题意；
B、原式不能分解，不符合题意；
C、原式不是分解因式，不符合题意；
D、原式＝（m+2）2，符合题意，
故选：D．
此题主要考查了提公因式法，以及公式法在因式分解中的应用，要熟练掌握．
3、D
【解析】
根据平行四边形的性质进行判断即可.
【详解】
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠BDC＝∠ABD，故选项A正确；
∵四边形ABCD是平行四边形，
∴∠DAB＝∠DCB，故选项B正确；
∵四边形ABCD是平行四边形，
∴AD＝BC，故选项C正确；
由四边形ABCD是平行四边形，不一定得出AC⊥BD，
故选D.
本题主要考查平行四边形的性质，掌握平行四边形的相关知识点是解答本题的关键．
4、C
【解析】
根据分式的基本性质逐一进行判断即可得答案．
【详解】
A、，故此选项不成立；
B、＝＝a+b，故此选项不成立；
C、＝＝a+1，故此选项成立；
D、＝＝﹣，故此选项不成立；
故选：C．
本题考查了分式的基本性质，分式的分子和分母同时乘以或除以同一个不为0的整式，分式的值不变；熟练掌握分式的基本性质是解题关键．
5、A
【解析】
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【详解】
解：0.000000102m＝1.02×10﹣7m；
故选A．
本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
6、B
【解析】
解：由题意得，
∵△ABC∽△A′B′C′，△A′B′C′的周长是△ABC的一半
∴位似比为2
∴S△ABC=4S△A′B′C=24cm2，
∴AB边上的高等于6cm．
故选B．
7、A
【解析】
根据师生的总费用，可得函数关系式．
【详解】
解：一名老师带领x名学生到动物园参观，已知成人票每张30元，学生票每张10元．设门票的总费用为y元，则y与x的函数关系为y=10x+30，
故选A．
本题考查了函数关系式，师生的总费用的等量关系是解题关键．
8、B
【解析】
解：设两个阴影部分三角形的底为AD，CB，高分别为h1，h2，则h1+h2为平行四边形的高，
∴
=4
故选：B
本题主要考查了三角形的面积公式和平行四边形的性质(平行四边形的两组对边分别相等).要求能灵活的运用等量代换找到需要的关系．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
连接AA′，BB′，作线段AA′，BB′的垂直平分线，两条垂直平分线交于点D，点D即为所求．
【详解】
解：连接AA′，BB′，作线段AA′，BB′的垂直平分线，两条垂直平分线交点即为点D，如图，旋转中心D的坐标为（3，0）．
故答案为：（3，0）．
本题考查了旋转的性质，掌握对应点连线的垂直平分线的交点就是旋转中心是解题的关键．
10、对应角相等的三角形全等
【解析】
根据逆命题的概念，交换原命题的题设与结论即可的出原命题的逆命题.
【详解】
命题“全等三角形对应角相等”的题设是“全等三角形”，结论是“对应角相等”，
故其逆命题是对应角相等的三角形是全等三角形．
故答案是：对应角相等的三角形是全等三角形．
考查了互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．
11、5cm
【解析】
根据角平分线的性质、RT△中，30°所对的直角边等于斜边的一般，本题得以解决．
【详解】
解：由题意可得，
OC为∠MON的角平分线，
∵，OC平分∠AOB，∴∠MOP=∠MON=30°,
∵，∴∠ODP=90°,
∵OP=10，
∴PD=OP=5，
故答案为：5cm．
本题考查了角平分线的性质及直角三角形的性质，解题的关键是掌握直角三角形的性质．
12、y=3x-1
【解析】
∵y=3x+1的图象沿y轴向下平移2个单位长度，
∴平移后所得图象对应的函数关系式为：y=3x+1﹣2，即y=3x﹣1．
故答案为y=3x﹣1．
13、-1
【解析】
方程kx+b=0的解其实就是当y=0时一次函数y=kx+b与x轴的交点横坐标．
【详解】
由图知：直线y=kx+b与x轴交于点（-1，0），
即当x=-1时，y=kx+b=0；
因此关于x的方程kx+b=0的解为：x=-1．
故答案为：-1
本题主要考查了一次函数与一次方程的关系，关键是根据方程kx+b=0的解其实就是当y=0时一次函数y=kx+b与x轴的交点横坐标解答．
三、解答题（本大题共5个小题，共48分）
14、（1）证明见解析（2）-1
【解析】
（1）先由旋转的性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，得出△ACF≌△ABE，从而得出BE=CF；
（2）由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的性质得∠AEB=∠ABE，根据平行线得性质得∠ABE=∠BAC=45°，所以∠AEB=∠ABE=45°，于是可判断△ABE为等腰直角三角形，所以BE=AC=，于是利用BD=BE﹣DE求解．
【详解】
（1）∵△AEF是由△ABC绕点A按顺时针方向旋转得到的，
∴AE=AB，AF=AC，∠EAF=∠BAC，
∴∠EAF+∠BAF=∠BAC+∠BAF，
即∠EAB=∠FAC，
在△ACF和△ABE中，
△ACF≌△ABE
BE=CF.
（2）∵四边形ACDE为菱形，AB=AC=1，
∴DE=AE=AC=AB=1，AC∥DE，
∴∠AEB=∠ABE，∠ABE=∠BAC=45°，
∴∠AEB=∠ABE=45°，
∴△ABE为等腰直角三角形，
∴BE=AC=，
∴BD=BE﹣DE=．
考点：1．旋转的性质；2．勾股定理；3．菱形的性质．
15、（1）；（2）
【解析】
（1）通过分母有理化进行计算；
（2）先分母有理化，然后合并即可．
【详解】
解：（1）
（2）原式

.
考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
16、见解析
【解析】
直接利用全等三角形的判定方法得出△ABC≌△ECD，即可得出答案．
【详解】
证明：∵AB∥DC，
∴∠B=∠ECD，
在△ABC和△ECD中，
，
∴△ABC≌△ECD（SAS），
∴∠A=∠E（全等三角形的对应角相等）．
本题考查了全等三角形的判定与性质，解题的关键是熟练的掌握全等三角形的判定与性质.
17、（1）时，四边形是平行四边形；（2）见解析；（3）见解析.
【解析】
（1）当AC∥DE时，因为AC=DE，推出四边形ACDE是平行四边形，利用平行四边形的性质即可解决问题．
（2）如图2中，作DM⊥FM于M，BN⊥FM交FM的延长线于N．利用全等三角形的性质证明BN=DM，再证明△BNG≌△DMG（AAS）即可解决问题．
（3）如图3中，延长CM到K，使得MK=CM，连接AK．KM．想办法证明△BCD≌△CAK（SAS），即可解决问题．
【详解】
（1）解：如图1-1中，连接AE．
当AC∥DE时，∵AC=DE，
∴四边形ACDE是平行四边形，
∴∠ACE=∠CED，
∵CE=CD，∠ECD=90°，
∴∠CED=1°，
∴α=∠ACE=1°．
故答案为1．
（2）证明：如图2中，作DM⊥FM于M，BN⊥FM交FM的延长线于N．
∵CF⊥AE，DM⊥FM，
∴∠CFE=∠CMD=∠ECD=90°，
∴∠ECF+∠CEF=90°，∠ECF+∠DCM=90°，
∴∠CEF=∠DCM，∵CE=CD，
∴△CFE≌△DMC（AAS），
∴DM=CF，
同法可证：CF=BN，
∴BN=DM，
∵BN⊥FM，
∴∠N=∠DMG=90°，
∵∠BGN=∠DGM，
∴△BNG≌△DMG（AAS），
∴BG=DG，
∴点G是BD的中点．
（3）证明：如图3中，延长CM到K，使得MK=CM，连接AK．KM．
∵AM-ME，CM=MK，
∴四边形ACEK是平行四边形，
∴AK=CE=CD，AK∥CE，
∴∠KAC+∠ACE=180°，
∵∠ACE+∠BCD=180°，
∴∠BCD=∠KAC，
∵CA=CB，CD=AK，
∴△BCD≌△CAK（SAS），
∵∠ACK=∠CBD，
∵∠ACK+∠BCN=90°，
∴∠CBD+∠BCN=90°，
∴∠CNB=90°，
∴CN⊥BD．
本题属于四边形综合题，考查了等腰直角三角形的性质，平行四边形的判定和性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题
18、（1）证明见解析；（2）成立；（3）①12；②7.1
【解析】
（1）先判断出∠B=∠CDF，进而判断出△CBE≌△CDE，即可得出结论；
（2）先判断出∠BCE=∠DCF，进而判断出∠ECF=∠BCD=90°，即可得出∠GCF=∠GCE=41°，得出△ECG≌△FCG即可得出结论；
（3）先判断出矩形ABCH为正方形，进而得出AH=BC=AB，
①根据勾股定理得，AD=8，由（1）（2）知，ED=BE+DH，设BE=x，进而表示出DH=10-x，用AH=AB建立方程即可得出结论；
②由（1）（2）知，ED=BE+DH，设DE=a，进而表示出DH=a-3，AD=12-a，AE=6，根据勾股定理建立方程求解即可得出结论．
【详解】
解：（1）在正方形ABCD中，
∵BC=CD，∠B=∠ADC，
∴∠B=∠CDF，
∵BE=DF，
∴△CBE≌△CDF，
∴CE=CF；
（2）成立，由（1）知，△CBF≌△CDE，
∴∠BCE=∠DCF，
∴∠BCE+∠ECD=∠DCF+∠ECD，
∴∠ECF=∠BCD=90°，
∵∠GCE=41°，
∴∠GCF=∠GCE=41°，
∵CE=CF，∠GCE=∠GCF，GC=GC，
∴△ECG≌△FCG，
∴GE=GF，
∴GE=DF+GD=BE+GD；
（3）如图2，过点C作CH⊥AD交AD的延长线于H，
∵AD∥BC，∠B=90°，
∴∠A=90°，
∵∠CHA=90°，
∴四边形ABCH为矩形，
∵AB=BC，
∴矩形ABCH为正方形，
∴AH=BC=AB，
①∵AE=6，DE=10，根据勾股定理得，AD=8，
∵∠DCE=41°，
由（1）（2）知，ED=BE+DH，
设BE=x，
∴10+x=DH，
∴DH=10-x，
∵AH=AB，
∴8+10-x=x+6，
∴x=6，
∴AB=12；
②∵∠DCE=41°，
由（1）（2）知，ED=BE+DH，
设DE=a，
∴a=3+DH，
∴DH=a-3，
∵AB=AH=9，
∴AD=9-（a-3）=12-a，AE=AB-BE=6，
根据勾股定理得，DE2=AD2+AE2，
即：（12-a）2+62=a2，∴a=7.1，
∴DE=7.1．
本题是四边形综合题，考查了矩形的判定，正方形的判定和性质，勾股定理，全等三角形的判定和性质，判断出△ECG≌△FCG是解本题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、y＝1x+1．
【解析】
根据平移k不变，b值加减即可得出答案．
【详解】
y＝1x－1向上平移4个单位则：
y＝1x－1＋4＝1x＋1，
故答案为：y＝1x＋1.
本题考查图形的平移变换和函数解析式之间的关系，平移后解析式有这样一个规律“左加右减，上加下减”．
20、87.1
【解析】分析：运用加权平均数的公式直接计算．用80分，90分，91分，分别乘以3，3，2，再用它们的和除以8即可．
详解：由题意知，总成绩=（80×3+90×3+91×2）÷（3+3+2）=87.1（分）．
故答案为：87.1．
点睛：本题考查的是加权平均数的求法．本题易出现的错误是直接求出80，90，91的平均数．
21、1
【解析】
分别求出正方形ABCD的内角∠ABC和正六边形BEFGHC的内角∠CBE的度数，进一步即可求出答案．
【详解】
解：∵四边形ABCD是正方形，
∴∠ABC=90°，
∵六边形BEFGHC是正六边形，
∴∠CBE=，
∴∠ABE=360°－(∠ABC+∠CBE)=360°－(90°+120°)=1°．
故答案为：1．
本题主要考查了正多边形的内角问题，属于基础题型，熟练掌握多边形的内角和公式是解题的关键．
22、
【解析】
先逐项化简，再进一步计算即可.
【详解】
原式=-1-3+1= .
故答案为：.
本题考查了实数的混合运算，正确化简各数是解答本题的关键.
23、m（m﹣9）
【解析】
直接提取公因式m即可．
【详解】
解：原式＝m（m﹣9）．
故答案为：m（m﹣9）
此题主要考查了提公因式法分解因式，关键是正确找出公因式．
二、解答题（本大题共3个小题，共30分）
24、（1）原式＝5；（2）原式＝8
【解析】
（1）根据完全平方公式、二次根式的乘法和加法可以解答本题；
（2）根据a、b的值可以求得a+b、a-b的值，从而可以求得所求式子的值．
【详解】
解：（1）
=
=5
（2）∵，
∴，
∴
=
=
本题考查二次根式的化简求值，解答本题的关键是明确二次根式化简求值的方法．
25、（1）见解析；（2）.
【解析】
（1）画树状图或列表都可以列出两次摸球出现的所有可能结果共有6种；（2）利用（1）中的结果可确定摸出的两个球号码之和等于5的结果有2种，然后利用概率公式计算即可．
【详解】
解：（1）根据题意，可以画出如下的树形图：
从树形图可以看出，摸出两球出现的所有可能结果共有6种；
（2）设两个球号码之和等于5为事件．
摸出的两个球号码之和等于5的结果有2种，它们是：．
．
考点：简单事件的概率．
26、 (1)1400；(2)；(3)小芳的骑车速度至少为．
【解析】
（1）直接利用反比例函数图象上点的坐标得出小芳家与学校之间的距离；
（2）利用待定系数法求出反比例函数解析式；
（3）利用y=8进而得出骑车的速度．
【详解】
(1)小芳家与学校之间的距离是：()；
(2)设，当时，，
解得：，
故与的函数表达式为：；
(3)当时，，
，在第一象限内随的增大而减小，
小芳的骑车速度至少为．
此题主要考查了反比例函数的应用，正确得出函数关系式是解题关键．
题号
一
二
三
四
五
总分
得分