山东省泰安市泰山区2024--2025学年上学期九年级数学第一次月考试卷

这是一份山东省泰安市泰山区2024--2025学年上学期九年级数学第一次月考试卷，共11页。试卷主要包含了在中，若，则的度数是，如图，在中，，，，则的长是等内容，欢迎下载使用。
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．做选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。
第I卷（选择题）
一、选择题（共12小题，每题4分，共48分）
1．如图，在中，，，，则的值为（ ）
A．B．C．D．
2．河堤横断面如图所示，米，迎水坡的坡度是1：2（坡度是坡面的铅直高度与水平宽度之比），则的长为（ ）
A．米B．米C．15米D．10米
3．点在函数图象上，下列说法中错误的是（ ）
A．它的图象分布在二、四象限B．当时，的值随的增大而增大
C．当时，的值随的增大而减小D．它的图象过点
4．在中，若，则的度数是（ ）
A．B．C．D．
5．已知三个点，，在反比例函数的图象上，其中，下列结论中正确的是（ ）
A．B．C．D．
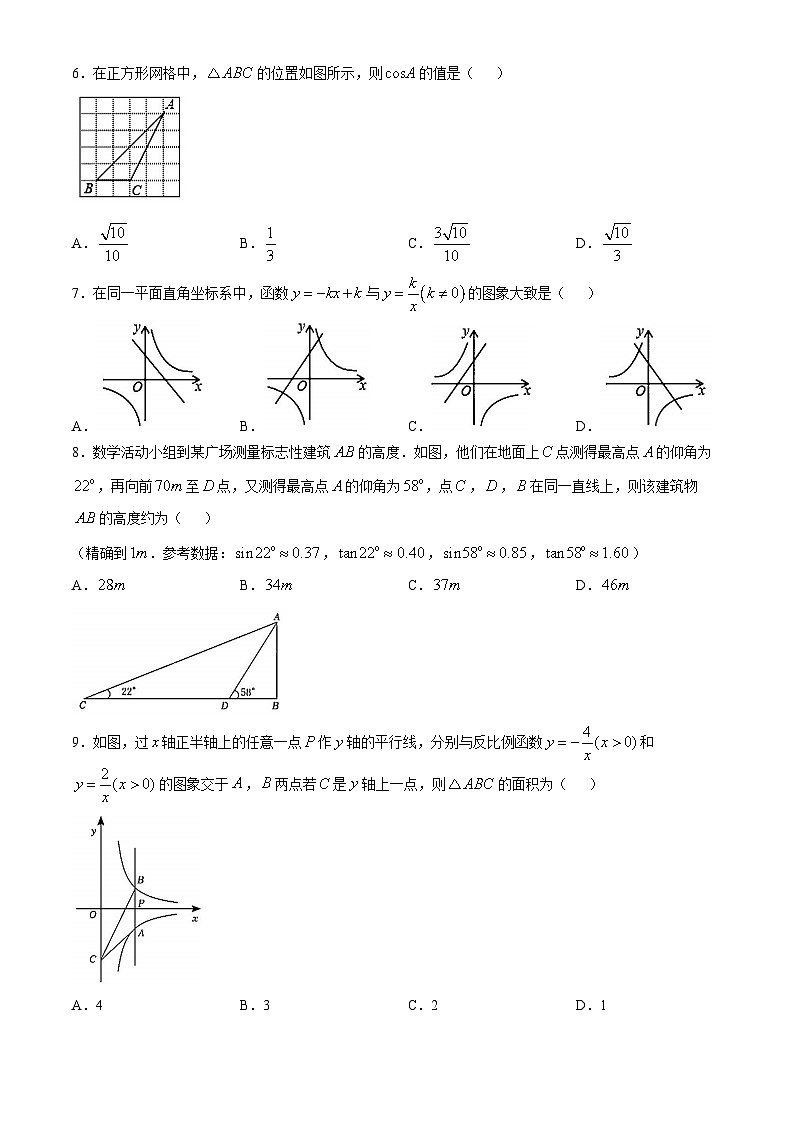
6．在正方形网格中，的位置如图所示，则的值是（ ）
A．B．C．D．
7．在同一平面直角坐标系中，函数与的图象大致是（ ）
A．B．C．D．
8．数学活动小组到某广场测量标志性建筑的高度．如图，他们在地面上点测得最高点的仰角为，再向前至点，又测得最高点的仰角为，点，，在同一直线上，则该建筑物的高度约为（ ）
（精确到．参考数据：，，，）
A．B．C．D．
9．如图，过轴正半轴上的任意一点作轴的平行线，分别与反比例函数和的图象交于，两点若是轴上一点，则的面积为（ ）
A．4B．3C．2D．1
10．如图，在中，，，，则的长是（ ）
A．B．C．D．9
11．反比例函数的图象上有，两点．下列正确的选项是（ ）
A．当时，B．当时，
C．当时，D．当时，
12．如图，正方形的顶点，在轴上，反比例函数的图象经过点和的中点，若，则的值是（ ）
A．4B．5C．6D．9
第II卷（非选择题）
二、填空题（共6小题，每题4分，共24分）
13．函数是关于的反比例函数，则__________．
14．已知等腰三角形的两边长为5和6，则该等腰三角形底角的余弦值为__________．
15．如图，在平面直角坐标系中，过原点的直线交反比例函数图象于，两点，轴于点，的面积为6，则的值为__________．
16．已知点为直线与双曲线的交点，则的值等于__________．
17．如图所示，某数学兴趣小组利用无人机测大楼的高度，无人机在空中点处，测得点距地面上点100米，点处俯角为，楼顶点处的俯角为，已知点与大楼的距离为80米（点，，，在同一平面内），则大楼的高度__________米．（结果精确到0.1米，参考数据：）．
18．如图，在平面直角坐标系中，为原点，点在第一象限，点是轴正半轴上一点，，双曲线过点，交于点，连接，若，则的值是__________．
三、解答题（共7小题，共78分）
19．（每题4分，共8分）计算：
（1）；
（2）．
20．（10分）如图，在平面直角坐标系中，一次函数的图像与轴、轴分别交于点、，与反比例函数的图像交于点．已知点坐标为，点坐标为．
（1）求反比例函数及一次函数的表达式；
（2）点在线段上，过点且平行于轴的直线交于点，交反比例函数图像于点．当时，求点的坐标．
21．（10分）某兴趣小组开展了测量电线塔高度的实践活动．如图所示，斜坡的坡度，，在处测得电线塔顶部的仰角为，在处测得电线塔顶部的仰角为．
（1）求点离水平地面的高度．
（2）求电线塔的高度（结果保留根号）．
22．（10分）拉杆箱是外出旅行常用工具．某种拉杆箱示意图如图所示（滚轮忽略不计），箱体截面是矩形，的长度为，两节可调节的拉杆长度相等，且与在同一条直线上．如图1，当拉杆伸出一节时，与地面夹角；如图2，当拉杆伸出两节（、）时，与地面夹角，两种情况下拉杆把手点距离地面高度相同．求每节拉杆的长度．
（参考数据：，，，）
23．（12分）如图为某景区平面示意图，为景区大门，，，分别为三个风景点．经测量，，，在同一直线上，且，在的正北方向，米，点在点的南偏东方向，在点的东南方向．（参考数据：，）
（1）求，两地的距离；（结果精确到0.1米）
（2）大门在风景点的南偏西方向，景区管理部门决定重新翻修之间的步道，求间的距离．
24．（14分）如图，一次函数的图象与反比例函数的图象交于点，与轴交于点．
（1）求，的值；
（2）直线过点，与反比例函数图象交于点，与轴交于点，，连接．
①求的面积；
②利用图象信息，直接写出不等式的解集．
③点在反比例函数的图象上，点在轴上，若以点，，，为顶点的四边形是平行四边形，请求出所有符合条件的点坐标．
25．（14分）探究：是否存在一个新矩形，使其周长和面积为原矩形的2倍、倍、倍？
（1）若该矩形是边长为2的正方形，是否存在一个正方形，使其周长和面积都是它的2倍？__________（填“存在”或“不存在”）．
（2）继续探究，若该矩形长为3，宽为2，是否存在一个矩形，使其周长和面积都为该矩形的2倍？
小明同学有以下思路：
设新矩形长和宽为，，则依题意，，联立得，再探究根的情况：
小慧同学认为：也可用反比例函数与一次函数图象证明，如图：，．则是否存在一个新矩形为原矩形周长和面积的2倍？请你结合小明和小慧的思路做出判断并说明理由．
（3）根据此方法，请你探究是否存在一个新矩形，使其周长和面积都为这个长为3，宽为2的矩形的倍？若存在，用图象表达；
（4）是否存在一个新矩形，使其周长和面积为长为3，宽为2的矩形的倍？请写出当结论成立时的取值范围．
初四上学期数学第一次月考答案
一、选择题（共12小题）
1．D 2．D 3．C 4．C 5．C 6．C 7．A 8．C
9．B 10．B 11．A 12．D
二、填空题（共6小题）
13．2 14．或． 15．． 16．． 17．69.3． 18．
三、解答题（共7小题）
19．解：（1）
；
（2）
．
20．解：（1）把点代入得，，解得，
反比例函数的表达式为，
把点，点代入得，
，解得，
一次函数的表达式为；
（2）设，
平行于轴，，，
，，解得，，点的纵坐标为，
把代入得，，点的坐标为．
21．解：（1）由题意得：，
斜坡的坡度，，
在中，，，，
，，
点离水平地面的高度为；
（2）过点作，垂足为，由题意得：，，
设米，米，米，
在中，，
（米），
在中，，
米，
解得：，
米，
电线塔的高度为米．
22．解：如图1，作，垂足为，设，则，
，，
如图2，作，垂足为，则，，
，，，
解得：．
答：每节拉杆的长度为．
23．解：（1）过点作于点，
由题意知，，
，，
，，
在中，米，
（米），
（米）．
答：、两地的距离约为339.4米；
（2）过点作于点，
由（1）得（米），
，，，
，，
在中，，，
（米），
在中，，
（米），（米），
24．解：（1）把，代入得，，，
把，代入得，，；
（2）点，点的纵坐标是0，，
点的纵坐标是，把代入得，
，
（2）①如图1，
作轴于，交于，
当时，，
，，
，
②
③设，，，．
当为对角线时，，，
当为对角线时
解得，，，舍去
当为对角线时
解得：，
综上点坐标为或．
25．解：（1）由题意得，给定正方形的周长为8，面积为4，
若存在新正方形满足条件，则新正方形的周长为16，面积为8，
对应的边长为：4和，不符合题意，
不存在新正方形的周长和面积是边长为2的正方形的2倍．
故答案为：不存在．
（2）从图象看来，函数和函数图象在第一象限有两个交点，
存在新矩形，使得周长和面积是原矩形的2倍．
（3）设新矩形长和宽为、，则依题意，，
联立，得：，
，
此方程无解，
不存在新矩形使得其周长和面积为原矩形的倍．
（4）设新矩形长和宽为、，则依题意，，
联立，得：，
，
设方程的两根为，，
当即时，，，
解得：或（舍），
当时，存在新矩形的周长和面积均为原矩形的倍．