辽宁省大连市第八十中学2024-2025学年九年级上学期10月月考数学试卷

这是一份辽宁省大连市第八十中学2024-2025学年九年级上学期10月月考数学试卷，共11页。试卷主要包含了抛物线的顶点坐标是，把二次函数化成的形式是，对二次函数的性质描述正确的是等内容，欢迎下载使用。

注意事项
1.请在答题卡上作答，在试卷上作答无效。
2.本试卷共三大题，23小题，满分120分。考试时间120分钟。
第一部分 选择题（共30分）
一、选择题（本题共10小题，每小题3分，共30分）
1.下列函数是二次函数的是（ ）
A.B.C.D.
2.二次函数的图象大致是（ ）
A. B. C. D.
3.抛物线的顶点坐标是（ ）
A.B.C.D.
4.把抛物线向左平移2个单位，再向上平移1个单位，所得的抛物线的解析式是（ ）
A.B.C.D.
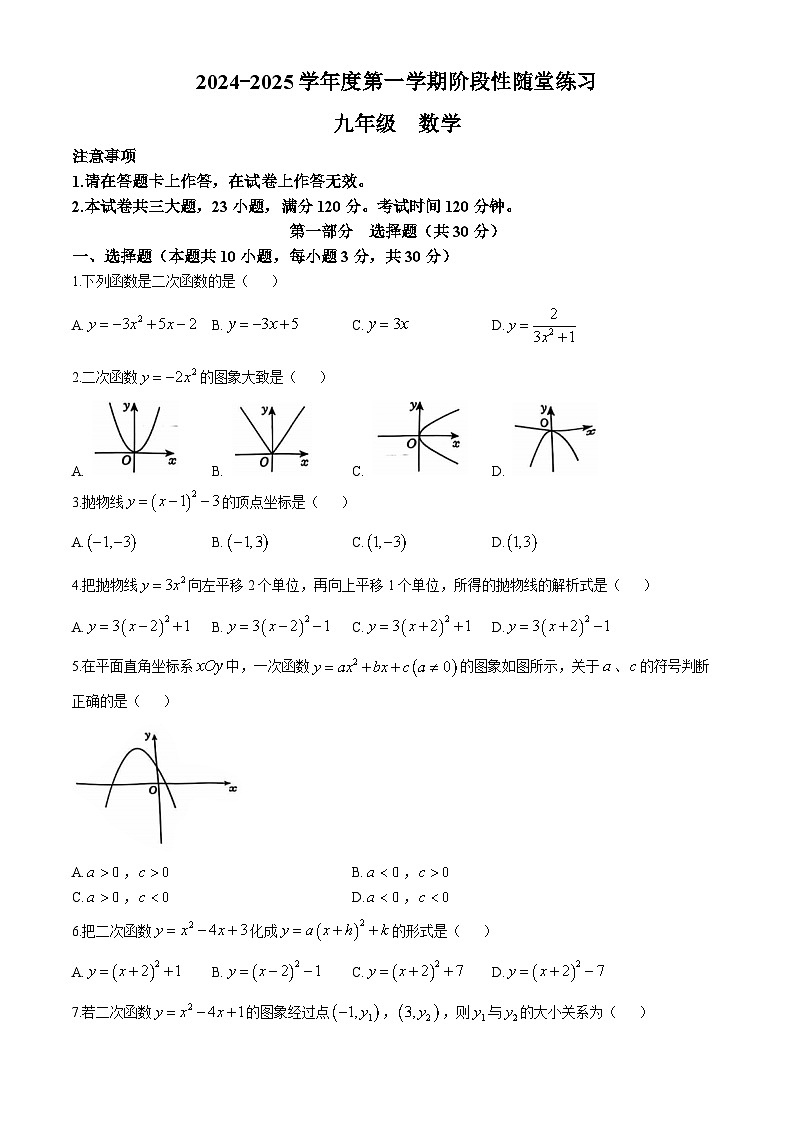
5.在平面直角坐标系中，一次函数的图象如图所示，关于、的符号判断正确的是（ ）
A.，B.，
C.，D.，
6.把二次函数化成的形式是（ ）
A.B.C.D.
7.若二次函数的图象经过点，，则与的大小关系为（ ）
A.B.C.D.不能确定
8.下表示用计算器探索函数时所得的数值：
则方程的一个解的取值范围为（ ）
A.B.C.D.
9.把一根长为50cm的铁丝弯成一个长方形，设这个长方形的一边长为，它的面积为，则与之间的函数关系式为（ ）
A.B.C.D.
10.对二次函数的性质描述正确的是（ ）
A.函数图象开口朝下B.当时，随的增大而减小
C.该函数图象与轴的交点位于轴负半轴D.该函数图象的对称轴在轴左侧
第二部分 非选择题（共90分）
二、填空题（本题共5小题，每小题3分，共15分）
11.函数的最大值为______.
12.抛物线的部分图象如图所示，其与轴的一个交点坐标为，对称轴为直线，抛物线与轴的另一个交点坐标为______.
13.如图，在平面直角坐标系中，抛物线与轴相交于点，，点的坐标为，若点在抛物线上，则的长为______.
14.如图，在期末体育测试中，小朱掷出的实心球的飞行高度（米）与水平距离（米）之间的关系大致满足二次函数，则小朱本次投掷实心球的成绩为米______.
15.如图，菱形的边长为2，点在轴的负半轴上，抛物线过点.若，则______.
三、解答题（本大题含8道小题，共75分）
16.（本题满分8分）
已知二次函数的图象经过和.
（1）求该抛物线的解析式；
（2）求抛物线的顶点坐标.
17.（本题满分9分）
二次函数的解析式为.
（1）求证：无论取何值，抛物线总与轴有交点；
（2）当时，
①求抛物线与轴的两个交点的坐标；
②当函数值大于0时，请直接写出的取值范围.
18.（本题满分9分）
如图，掷实心球是大连市中考体育考试中“五选二”当中的一个项目，一名男生掷实心球，已知实心球出手时离地面2米，当实心球行进的水平距离为4米时实心球被掷得最高，此时实心球离地面3.6米，设实心球行进的路线是如图所示的一段抛物线.
（1）求实心球行进的高度（米）与行进的水平距离（米）之间的函数关系式；
（2）如果实心球考试优秀成绩为9.6米，那么这名男生在这次考试中成绩是否能达到优秀？请说明理由.
19.（本题满分9分）
如图，抛物线与轴交于，对称轴是直线，直线经过点且与抛物线交于另一点.
（1）求抛物线的解析式；
（2）若是位于直线上方的抛物线上的一个动点，连接，，求的面积的最大值.
20.（本题满分9分）
某超市以每件13元的价格购进一种商品，销售时该商品的销售单价不低于进价且不高于18元.经过市场调查发现，该商品每天的销售量（件）与销售单价（元）之间满足如图所示的一次函数关系.
（1）求与之间的函数关系式；
（2）销售单价定为多少时，该超市每天销售这种商品所获的利润最大？最大利润是多少？
21.（本题满分9分）
在平面直角坐标系中，已知抛物线.
（1）求抛物线的对称轴；
（2）当时，设抛物线与轴交于，两点（点在点左侧），顶点为，若为等边三角形，求的值；
（3）过（其中）且垂直轴的直线与抛物线交于，两点.若对于满足条件的任意值，线段的长都不小于1，结合函数图象，直接写出的取值范围.
22.（本题满分10分）
【发现问题】城市的许多街道是相互垂直或平行的，因此往往不能沿直线行走到目的地，只能按直角拐弯的方式行走.我们可以按照街道的垂直和平行方向建立平面直角坐标系，对两点和，用以下方式定义两点间的“折线距离”：.
（1）①已知点，则______；
②函数的图象如图1，是图象上一点，若，则点的坐标为______；
（2）如图2，菱形顶点的坐标是，，.小明发现：菱形的边上会有两个点分别到原点的距离相等.若点在菱形的边上且，指出点在菱形的那条边上，并求出它的坐标.
【拓展运用】
（3）函数和函数的图象如图3，是函数图象上一点，是函数图象上一点，当和分别取到最小值时，求的值.
23.（本题满分12分）
如图1，在中，，点是边上一点，，将沿翻折至，与交于点.
（1）①通过测量，猜想并验证和的数量关系；
②求证：；
（2）如图2，过作交于点，若，，连接，求的长.
（3）如图3，若，求的长.
2024-2025学年度第一学期阶段性随堂练习
九年级数学
一、选择题
1.A 2.D 3.C 4.C 5.B 6.B 7.A 8.C 9.D 10.D
二、填空题
11.8 12. 13.4 14.8 15.
三、解答题
16.（1）将，坐标分别代入解析式中得到
（2）由顶点坐标公式可知顶点坐标
17.（1）由根的判别式可知
所以抛物线与轴有交点。
（2）1当，得，当时，或3
所以交点坐标
2
18.（1）解：抛物线顶点
设，将代入
（2）当时，（舍）
答：成绩为10m，能达到优秀。
19.（1）对称轴为1，
令，，，
将代入，
（2） ，
过作轴
设，
当时，最大面积为.
20.（1）将，代入

（2）
当时，随增大而增大
当时，最大
答：售价18元时，最大利润700元。（9分）
21.（1）
（2）当时，
，
如图1，顶点
，
是等边三角形
，
（3），
22.（1）⑤（1分） ② （2分）
（2），，
设解析式为，，代入

当在上，设

点不能在点右侧
（3）解：设
，
当时，最小，
设 ，
当时，
当时，最小值为2
当时，
当时，最小值为3
当时，最小值为3
当时，最小
23.（1）
设，
（2），
，
设，，，
在中，，
（舍），
，，
（3）过作，取中点，连接
是的中位线
设，，

在中，，，

0
0.25
0.5
0.75
1
1.31
3