2024-2025学年浙江省丽水市“五校高中发展共同体”10月联考高一数学试题（含解析）

展开

这是一份2024-2025学年浙江省丽水市“五校高中发展共同体”10月联考高一数学试题（含解析），共14页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.下列关系中，正确的是( )
A. −2∈N+B. 32∈ZC. π∉QD. 5∉N
2.若命题p:∃x>0，x2−3x+2>0，则命题p的否定为( )
A. ∃x>0，x2−3x+2≤0B. ∃x≤0，x2−3x+2≤0
C. ∀x≤0，x2−3x+2>0D. ∀x>0，x2−3x+2≤0
3.若a,b,c为实数，且aA. ac2ab>b2D. ba>ab
4.为了加强家校联系，王老师组建了一个由学生，家长和教师组成的QQ群.已知该群中男学生人数多于女学生人数，女学生人数多于家长人数，家长人数多于教师人数，教师人数的两倍多于男学生人数.则该QQ群教师人数的最小值为( )
A. 3B. 4C. 5D. 6
5.若f(x)对于任意实数x都有2f(x)−f(1x)=2x+1，则f(12)=( )
A. 3B. 4C. 83D. 43
6.已知函数y=f(x)的定义域为[−1,4]，则y=f(2x+1) x−1的定义域为( )
A. [−1,32)B. (1,32]C. (1,9]D. [−5,32]
7.已知不等式ax2+bx+c>0的解集为(2,4)，则不等式cx2+bx+a<0的解集为( )
A. (14,12)B. (−∞,14)∪(12,+∞)
C. (2,4)D. (−∞,2)∪(4,+∞)
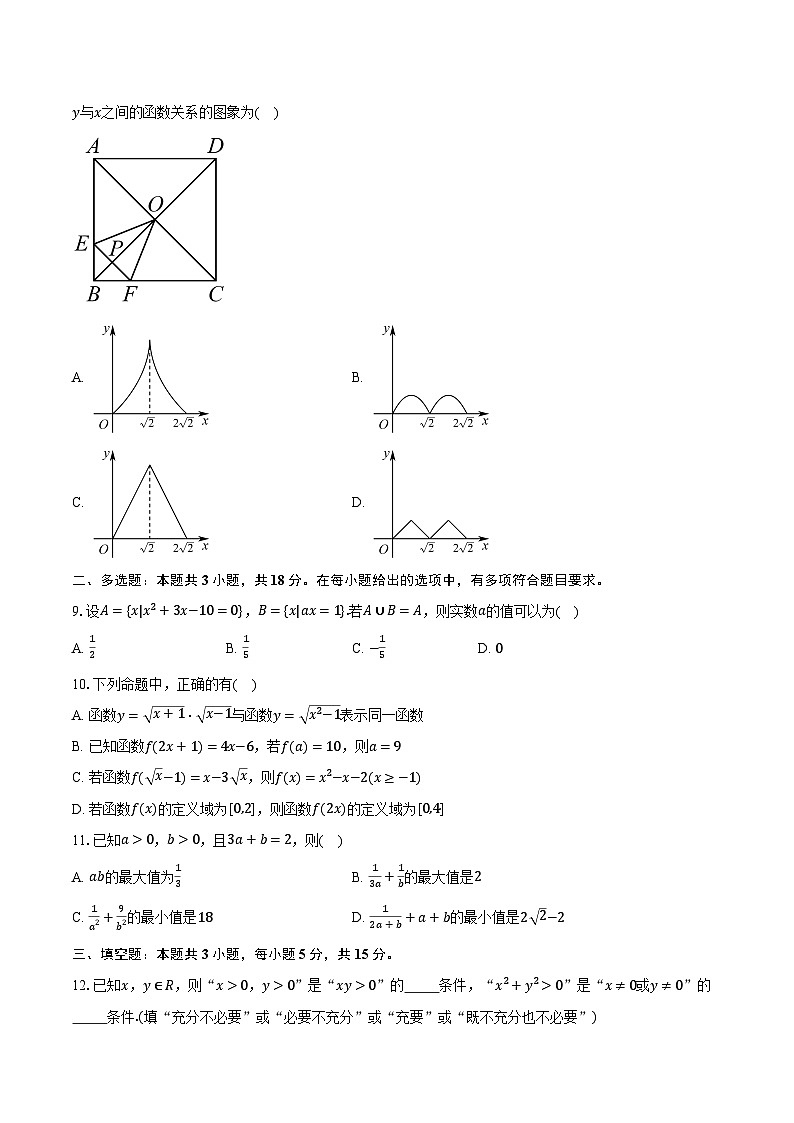
8.如图，在边长为2的正方形ABCD中，对角线AC与BD相交于点O，点P是BD上的一个动点，过点P作EF//AC，分别交正方形的两条边于点E，F，连接OE，OF，设BP=x，△OEF的面积为y，则能大致反映y与x之间的函数关系的图象为( )
A. B.
C. D.
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。
9.设A={x|x2+3x−10=0}，B={x|ax=1}.若A∪B=A，则实数a的值可以为( )
A. 12B. 15C. −15D. 0
10.下列命题中，正确的有( )
A. 函数y= x+1⋅ x−1与函数y= x2−1表示同一函数
B. 已知函数f(2x+1)=4x−6，若f(a)=10，则a=9
C. 若函数f( x−1)=x−3 x，则fx=x2−x−2x≥−1
D. 若函数fx的定义域为0,2，则函数f2x的定义域为0,4
11.已知a>0，b>0，且3a+b=2，则( )
A. ab的最大值为13B. 13a+1b的最大值是2
C. 1a2+9b2的最小值是18D. 12a+b+a+b的最小值是2 2−2
三、填空题：本题共3小题，每小题5分，共15分。
12.已知x，y∈R，则“x>0，y>0”是“xy>0”的条件，“x2+y2>0”是“x≠0或y≠0”的条件.(填“充分不必要”或“必要不充分”或“充要”或“既不充分也不必要”)
13.已知a∈R，函数f(x)=x2−4,x>2|x−3|+a,x⩽2，若f(f( 6))=3，则a= ．
14.已知函数f(x)=x2−2ax+1(a∈R)，若非空集合A={x|f(x)≤0}，B={x|f(f(x))≤1}，满足A=B，则实数a的取值范围是
四、解答题：本题共5小题，共60分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题12分)
已知全集U=R，集合A={x|x2−2x−3≤0}，集合B={x|x−1x+2>0}，集合C={x|m−1(1)求A∪B，A∩∁UB
(2)若A∩C=C，求实数m的取值范围．
16.(本小题12分)
已知x，y都是正数．
(1)若3x+2y=6，求xy的最大值;
(2)若x+2y=3，求1x+1y的最小值．
17.(本小题12分)
为摆脱美国政府针对中国高科技企业的封锁，加强自主性，某企业计划加大对芯片研发部的投入，据了解，该企业研发部原有100名技术人员，年人均投入60万元，现将这100名技术人员分成两部分：技术人员和研发人员，其中技术人员x名(x∈N*)，调整后研发人员的年人均投入增加4x%，技术人员的年人均投入调整为60(m−2x25)万元．
(1)要使这100−x名研发人员的年总投入不低于调整前的100名技术人员的年总投入，求调整后的技术人员的人数x最多为多少人?
(2)若技术人员在已知范围内调整后，必须研发人员的年总投入始终不低于技术人员的年总投入，求出正整数m的最大值．
18.(本小题12分)
已知关于的x不等式ax2+(a−1)x−1>0．
(1)若a=−2时，求不等式的解集;
(2)若a∈R，解这个关于x的不等式;
(3)∀x∈(0,+∞)，(ax−1)(x+1)>(2a+1)x−a恒成立，求a的范围．
19.(本小题12分)
《见微知著》谈到：从一个简单的经典问题出发，从特殊到一般，由简单到复杂，从部分到整体，由低维到高维，知识与方法上的类比是探索发展的重要途径，是发现新问题、新结论的重要方法．
例如，已知ab=1，求证：11+a+11+b=1．
证明：原式=abab+a+11+b=b1+b+11+b=1．
波利亚在《怎样解题》中也指出：“当你找到第一个蘑菇或作出第一个发现后，再四处看看，他们总是成群生长.”类似上述问题，我们有更多的式子满足以上特征．
请根据上述材料解答下列问题：
(1)已知ab=1，求11+a2+11+b2的值;
(2)若abc=1，解方程5axab+a+1+5bxbc+b+1+5cxca+c+1=1;
(3)若正数a，b满足ab=1，求M=11+a+11+2b的最小值．
答案和解析
1.【答案】C
【解析】【分析】
本题考查常用数集以及元素与集合的关系，是基础题．
【解答】
解：A:⋅2∉N+， A错误;
B:32∉Z，B 错误;
C:π∉Q， C正确;
D:5∈N， D错误
故选C．
2.【答案】D
【解析】【分析】
本题主要考查存在量词命题的否定，属基础题．
根据存在量词命题的否定为全称量词命题即可得到结论．
【解答】解：命题p:∃x>0，x2−3x+2>0为存在量词命题，
则该命题的否定为∀x>0，x2−3x+2≤0，
故选：D．
3.【答案】C
【解析】【分析】
本题考查了不等式的基本性质，考查了推理能力与计算能力，属于基础题．
利用不等式的基本性质即可得出．
【解答】
解：∵a则A.当c=0时，ac2B.由已知可得1a>1b，因此不成立；
C.由已知可得：a2>ab>b2，因此正确；
D.由已知可得：a2>b2，∴a2ab>b2ab，化为ab>ba，因此不成立．
故选：C．
4.【答案】B
【解析】【分析】本题主要考查了不等式的性质，属于基础题．
设男学生女学生人数分别为x，y人，教师人数为z，家长人数为m，x，y，z，m都是正整数，则x>yy>mm>z2z>x，进而可得答案．
【解答】解：设男学生女学生人数分别为x，y人，教师人数为z，家长人数为m，x，y，z，m都是正整数，
则由题意有x>yy>mm>z2z>x，即z此时y最小为6，m最小为5，x最小为7，
故选B．
5.【答案】A
【解析】【分析】
本题考查函数值的求法，考查运算求解能力，属于基础题．由f(x)对于任意实数x都有2f(x)−f(1x)=2x+1，列方程组，求出f(x)=43x+23x+1，由此能求出f(12)的值．
【解答】
解：∵f(x)对于任意实数x都有2f(x)−f(1x)=2x+1，
∴2f(x)−f(1x)=2x+12f(1x)−f(x)=2x+1，
解得f(x)=43x+23x+1，
∴f(12)=43×12+23×12+1=3．
故选：A．
6.【答案】B
【解析】【分析】
本题考查函数的定义域及其求法，是基础题．
由已知f(x)的定义域，再根据函数成立的条件建立不等式进行求解即可．
【解答】
解：因为y=f(x)的定义域是[−1,4]，
所以要使得y=f(2x+1) x−1有意义，
需满足−1≤2x+1≤4x−1>0，解得1则函数y=f(2x+1) x−1的定义域为是(1,32].
7.【答案】B
【解析】【分析】
本题考查了一元二次不等式的解集与相应的一元二次方程的根与系数的关系，考查了计算能力，属于中档题．
由不等式ax2+bx+c>0的解集是(2,4)可知：2，4是一元二次方程ax2+bx+c=0的实数根，且 a<0.然后利用根与系数的关系可得b=−6a,c=8a，代入不等式cx2+bx+a<0即可得出．
【解答】
解：因为不等式ax2+bx+c>0的解集是(2,4)，
所以2，4是一元二次方程ax2+bx+c=0的实数根，且a<0.
所以2+4=−ba,2×4=ca，
即b=−6a,c=8a．
所以不等式cx2+bx+a<0化为8ax2−6ax+a<0，即8x2−6x+1>0，
解得x<14或x>12．
所以不等式cx2+bx+a<0的解集为x|x<14或x>12．
故选B．
8.【答案】B
【解析】【分析】
本题考查函数图象的实际应用，属于中档题．
分点P在OB上和点P在DO上两种情况讨论，由面积公式可求y与x的函数关系，即可求解．
【解答】
解：当点P在OB上时，
∵四边形ABCD是正方形，边长为2，
∴AB=BC=2，AC⊥BD，∠ACB=∠CAB=45∘，
∴AC=2 2，BO=DO=AO=CO= 2，
∵EF//AC，
∴∠BAC=∠BEF=45∘，∠BFE=∠BCA=45∘，
∠AOB=∠EPB=90∘，
∴∠BEF=∠BFE，
∴BE=BF，
∵∠BPE=90∘，
∴BP=EP=FP=x，
∴OP= 2−x，
∴y=12×EF×OP=12×2x×( 2−x)
=−x2+ 2x，(0⩽x⩽ 2)
当点P在DO上时，
同理可得：y=−x2+3 2x−4，( 2故选：B．
9.【答案】ACD
【解析】【分析】
本题主要考查集合间的基本关系和集合运算，考查了分类讨论的数学思想，属于基础题．
根据A∪B=A可得：B⊆A，因为B={x|ax=1}，所以分B=⌀和B≠⌀两种情况进行讨论，进而求解即可．
【解答】解：因为A∪B=A，所以B⊆A，
又因为B={x|ax=1}，所以分B=⌀和B≠⌀两种情况进行讨论，
当B=⌀时，也即方程ax=1无解，所以a=0;
当B≠⌀时，方程ax=1有一解，即B={1a}，
因为A={2,−5}，所以1a=2或−5，
解得：a=12或−15，
综上可知：实数a的值为0或12或−15，
故选ACD．
10.【答案】BC
【解析】【分析】
本题考查同一函数的概念，函数求值，函数解析式以及抽象函数定义域，属于中档题．
分别求两个函数的定义域即可判断A；由函数解析式可得若f(a)=10，则2x+1=a4x−6=10即可判断B；利用配凑法可求解函数f(x)解析式，即可判断C；结合抽象函数定义域即可判断D．
【解答】
解：y=f(x)= x+1⋅ x−1的定义域是{x|x+1⩾0x−1⩾0}={x|x⩾1},
y=g(x)= x2−1的定义域是{x|x2−1⩾0}={x|x⩾1，或x⩽−1}，
两函数的定义域不同，故不是同一函数，A错误;
函数f(2x+1)=4x−6，若f(a)=10，则2x+1=a4x−6=10⇒x=4a=9，故B正确；
若函数f x−1=x−3 x=( x−1)2−( x−1)−2，则fx=x2−x−2x≥−1，故C正确；
若函数fx的定义域为0,2，则函数f2x中，0⩽2x⩽2⇒0⩽x⩽1，即函数f2x的定义域为0,1，故D错误．
故选BC．
11.【答案】AC
【解析】【分析】
本题考查利用基本不等式求最值，根据基本不等式的性质逐项进行判断即可。
【解答】
解：因为a>0，b>0，且3a+b=2，所以2 3ab≤2，所以ab≤13，
当且仅当3a=b=1时，等号成立，则A正确;
由题意可得13a+1b=12(3a+b)(13a+1b)=12(b3a+3ab+2)≥12×(2 b3a⋅3ab+2)=2，
当且仅当3a=b时，等号成立，则B错误;
因为ab≤13，所以1a2+9b2≥6ab≥18，当且仅当3a=b=1时，等号成立，则C正确;
由3a+b=2，得b=2−3a，对于D，由a>0b=2−3a>0，得012a+b+a+b=12a+2−3a+a+(2−3a)=12−a+2−2a=12−a+2(2−a)−2≥2 2−2，
当且仅当12−a=2(2−a)，当a=2± 22时，2± 22>23，矛盾，故等号取不到，故D错误.故选AC．
12.【答案】充分不必要；充要
【解析】【分析】
本题考查充分、必要、充要条件的判断，属于基础题．
根据充分条件和必要条件的概念，直接判断即可．
【解答】解：当x>0，y>0时，xy>0，满足充分性；
因为xy>0时，x>0，y>0或x<0，y<0，不满足必要性；
所以，y>0是的充分不必要条件；
当x2+y2>0，所以x≠0或y≠0，满足充分性；
当x≠0或y≠0时，x2+y2>0，满足必要性，
所以“x2+y2>0”是“x≠0或y≠0”的充要条件．
故答案为充分不必要；充要．
13.【答案】2
【解析】【分析】
本题考查求分段函数的函数值，属于基础题．
求出f( 6)=2，再代入f(f( 6))=3，即可求出结果．
【解答】解：因为 6>2，
所以f( 6)=6−4=2，
所以f(f( 6))=f(2)=1+a=3，解得a=2．
故答案为2．
14.【答案】[−1− 2,−1]
【解析】【分析】
本题考查集合相等、二次函数的最值、二次函数与一元二次方程、不等式的解的对应关系，属于中档题．
通过直接代入f(x)=x2−2ax+1，然后解一元二次不等式，通过分别判断两一元二次不等式的方程的Δ,Δ′，从而进行求解即可。
【解答】解：由f(f(x))≤1，可得(x2−2ax+1)2−2a(x2−2ax+1)+1≤1，
即(x2−2ax+1)(x2−2ax+1−2a)≤0，
由A=B，可得x2−2ax+1−2a≥0在R上恒成立，即△=4a2−4(1−2a)≤0，
解得−1− 2≤a≤−1+ 2，①
又集合A是非空集合，所以x2−2ax+1≤0在R上有解，
则Δ′=4a2−4⩾0，解得a⩽−1或a⩾1，②
综合① ②可得：a∈[−1− 2,−1]．
15.【答案】解：根据题意：(1)集合A={x|−1≤x≤3}，
集合B={x|x<−2或x>1}
A∪B={x|x<−2或x≥−1}，
A∩CUB={x|−1≤x≤1}
(2)因为A∩C=C，所以C⊆A，
若C=⌀，则m−1≥2m+1⇒m≤−2
若C≠⌀，则m−1<2m+1⇒m>−2时，可得m−1≥−12m+1≤3⇒0≤m≤1，
∴实数m的取值范围为{m|m≤−2或0≤m≤1}
【解析】本题考查了集合关系中的参数取值问题、交集及其运算和交、并、补集的混合运算，是基础题．
(1)先解不等式得出集合A、B，再由集合的运算可得结果；
(2)因为A∩C=C，所以C⊆A，分C=⌀和C≠⌀两种情况求解即可．
16.【答案】解：
(1)因为3x+2y=6，所以xy=16⋅3x⋅2y≤16×3x+2y22=32，
当且仅当3x=2y，即x=1，y=32时，等号成立.所以xy的最大值为32
(2)∵x+2y=3，
∴1=x3+2y3，
∴1x+1y=(1x+1y)(x3+2y3)
=13+23+x3y+2y3x
≥1+2 x3y⋅2y3x=1+2 23，
当且仅当x3y=2y3x，即x=3 2−3，y=3−3 22时取等号，
∴最小值为1+2 23．
【解析】本题主要考查基本不等式的应用，注意基本不等式的使用条件，以及等号成立的条件，式子的变形是解题的关键，属于基础题．
(1)由于3x+2y=6，再根据xy=16·3x·2y，利用基本不等式求得xy的最大值；
(2)由x+2y=3，得到1=x3+2y3，故1x+1y=(1x+1y)(x3+2y3)，利用基本不等式求得最小值．
17.【答案】解：(1)由题意得(100−x)⋅60⋅(1+4x%)≥100×60，x∈N*，
解得0故调整后的技术人员的人数最多为75人；
(2)由研发人员的年总投入始终不低于技术人员的年总投入有(100−x)⋅60⋅(1+4x%)≥x⋅60⋅(m−2x25)，
即(100x−1)(1+x25)≥m−2x25，
整理得m≤100x+x25+3，
∵100x+x25+3≥2 100x⋅x25+3=7，当且仅当x=50时等号成立，
∴m≤7，
故正整数m的最大值为7．
【解析】本题考查根据实际问题选择函数类型，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．
(1)根据题意列出不等式(100−x)⋅60⋅(1+4x%)≥100×60，x∈N*，求解即可得出答案；
(2)根据题意列出不等式(100−x)⋅60⋅(1+4x%)≥x⋅60⋅(m−2x25)，进行常变量分离，利用基本不等式，求解即可得出答案．
18.【答案】解：(1)a=−2时，−2x2−3x−1>0
⇒2x2+3x+1<0
⇒(2x+1)(x+1)<0
⇒−1则所求不等式的解集为：(−1,−12)；
(2)当a=0时，ax2+(a−1)x−1>0⇔−x−1>0⇒x<−1；
当a≠0时，ax2+(a−1)x−1>0⇔(ax−1)(x+1)=a(x−1a)(x+1)>0，
当a>0时，有1a>−1，则此时不等式解集为：(−∞,−1)∪(1a,+∞)；
当a<0，a(x−1a)(x+1)>0⇔(x−1a)(x+1)<0．
若1a<−1，即−1若1a>−1，即a<−1时，不等式解集为：(−1,1a)；
若1a=−1，即a=−1时，不等式解集为空集．
综上，a=0时，解集为(−∞,−1)；a=−1时，解集为⌀；
a>0时，解集为(−∞,−1)∪(1a,+∞)；
−1(3)(ax−1)(x+1)>(2a+1)x−a⇒a(x2−x+1)>2x+1，
因x2−x+1=(x−12)2+34≥34>0，则a>2x+1x2−x+1．
则题目等价于a>2x+1x2−x+1max,x>0．
令2x+1=t，因x>0，则t>1．
则2x+1x2−x+1=tt−122−t−12+1
=4tt2−4t+7=4t+7t−4
⩽42 t·7t−4=2 7−2=2 7+43，
当且仅当t=7t，即t= 7时等号成立，
所以a>2 7+43，即a的取值范围为2 7+43,+∞．
【解析】本题考查不等式的解法以及不等式的恒成立问题，考查运算求解能力，属于中档题．
(1)由题可得−2x2−3x−1>0，即可得答案；
(2)当a=0时，不等式变为一次不等式，当a≠0时，对ax2+(a−1)x−1=0分解因式，讨论根的大小即可得答案；
(3)由题，可得∀x>0，a>2x+1x2−x+1，利用换元法结合基本不等式可得答案．
19.【答案】解：(1)11+a2+11+b2=abab+a2+abab+b2=bb+a+aa+b=1;
(2)∵abc=1，
∴aab+a+1=aab+a+abc=1b+1+bc，
cca+c+1=cca+c+abc=1a+1+ab=abca+abc+ab=bc1+bc+b，
∴原方程可化为5xb+1+bc+5bxbc+b+1+5bcx1+bc+b=1，
即5(1+b+bc)xb+1+bc=1，即5x=1，∴x=15;
(3)∵正数a、b满足ab=1，
∴M=11+a+11+2b=abab+a+11+2b=bb+1+11+2b
=(b+1)−1b+1+11+2b=1−1b+1+11+2b=1−b(1+b)(1+2b)
=1−b2b2+3b+1=1−12b+3+1b≥1−12 2+3=2 2−2
当且仅当2b=1b，即b= 22时取等号，此时a= 2，符合题意，
∴M的最小值为2 2−2．
【解析】本题考查利用基本不等式求最值和类比推理，属于中档题．
(1)根据例子进行类比即可证明；
(2)将abc代入方程求解；
(3)由M=11+a+11+2b=abab+a+11+2b=1−12b+3+1b，利用基本不等式进行求解即可．

2024-2025学年浙江省丽水市“五校高中发展共同体”10月联考高一数学试题（含解析）

更专业

更丰富

更便捷

真低价

欢迎来到教习网