江苏省扬州市梅岭中学教育集团2024-2025学年八年级上学期10月月考数学试题

这是一份江苏省扬州市梅岭中学教育集团2024-2025学年八年级上学期10月月考数学试题，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（时间：120分钟）
一、选择题（每题3分，共计24分，把正确答案填在答题纸相应的位置上．）
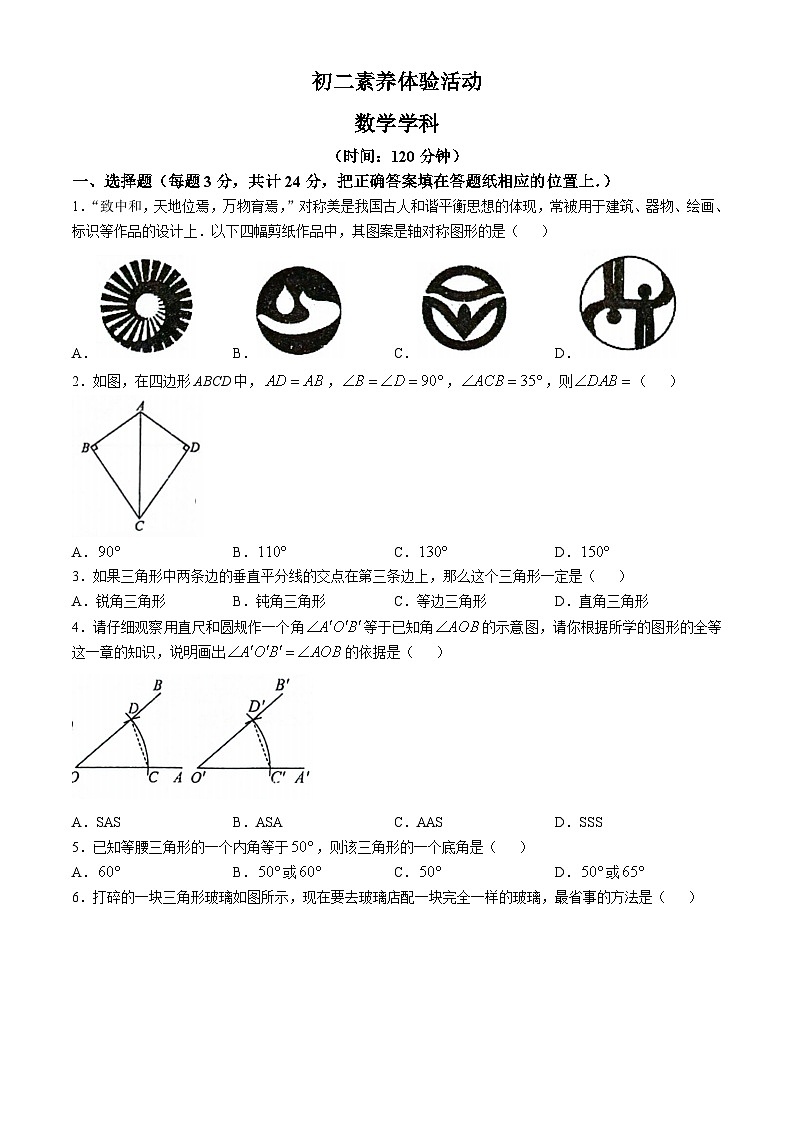
1．“致中和，天地位焉，万物育焉，”对称美是我国古人和谐平衡思想的体现，常被用于建筑、器物、绘画、标识等作品的设计上．以下四幅剪纸作品中，其图案是轴对称图形的是（ ）
A．B．C．D．
2．如图，在四边形ABCD中，，，，则（ ）
A．B．C．D．
3．如果三角形中两条边的垂直平分线的交点在第三条边上，那么这个三角形一定是（ ）
A．锐角三角形B．钝角三角形C．等边三角形D．直角三角形
4．请仔细观察用直尺和圆规作一个角等于已知角的示意图，请你根据所学的图形的全等这一章的知识，说明画出的依据是（ ）
A．SASB．ASAC．AASD．SSS
5．已知等腰三角形的一个内角等于，则该三角形的一个底角是（ ）
A．B．或C．D．或
6．打碎的一块三角形玻璃如图所示，现在要去玻璃店配一块完全一样的玻璃，最省事的方法是（ ）
A．带①②去B．带②③去C．带③④去D．带②④去
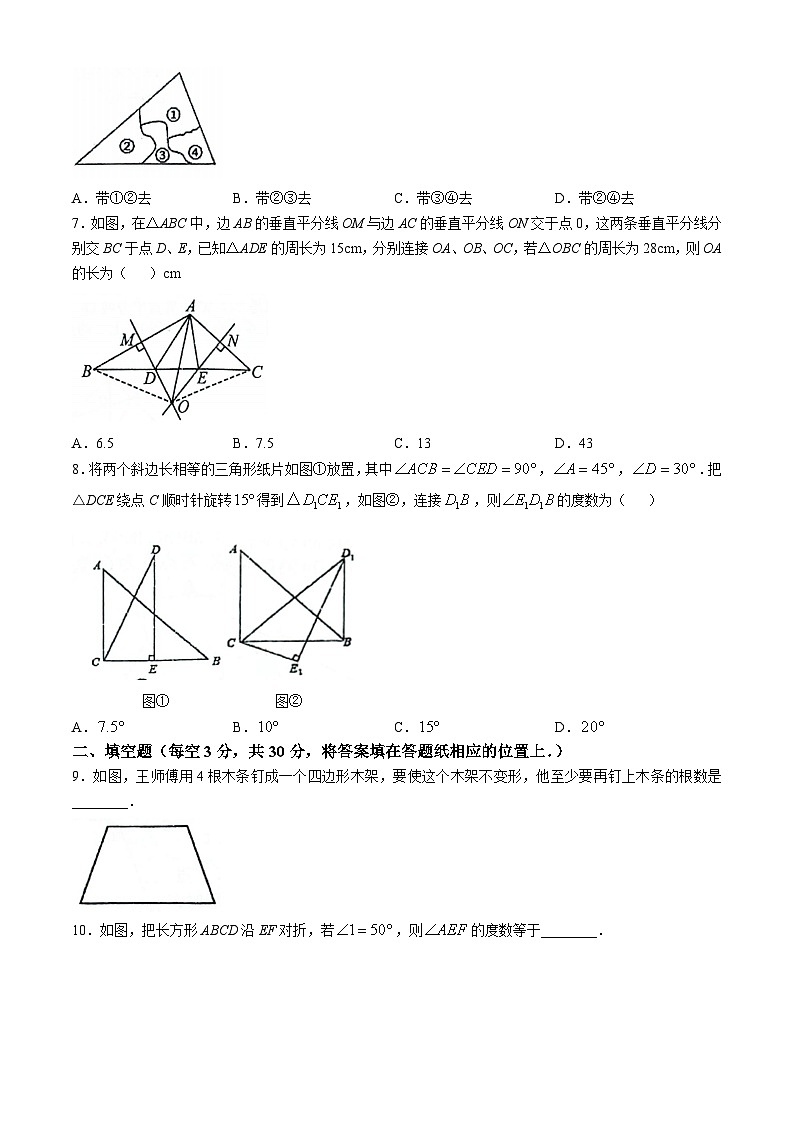
7．如图，在△ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点0，这两条垂直平分线分别交BC于点D、E，已知△ADE的周长为15cm，分别连接OA、OB、OC，若△OBC的周长为28cm，则OA的长为（ ）cm
A．6.5B．7.5C．13D．43
8．将两个斜边长相等的三角形纸片如图①放置，其中，，．把△DCE绕点C顺时针旋转得到，如图②，连接，则的度数为（ ）
图① 图②
A．B．C．D．
二、填空题（每空3分，共30分，将答案填在答题纸相应的位置上．）
9．如图，王师傅用4根木条钉成一个四边形木架，要使这个木架不变形，他至少要再钉上木条的根数是________．
10．如图，把长方形ABCD沿EF对折，若，则的度数等于________．
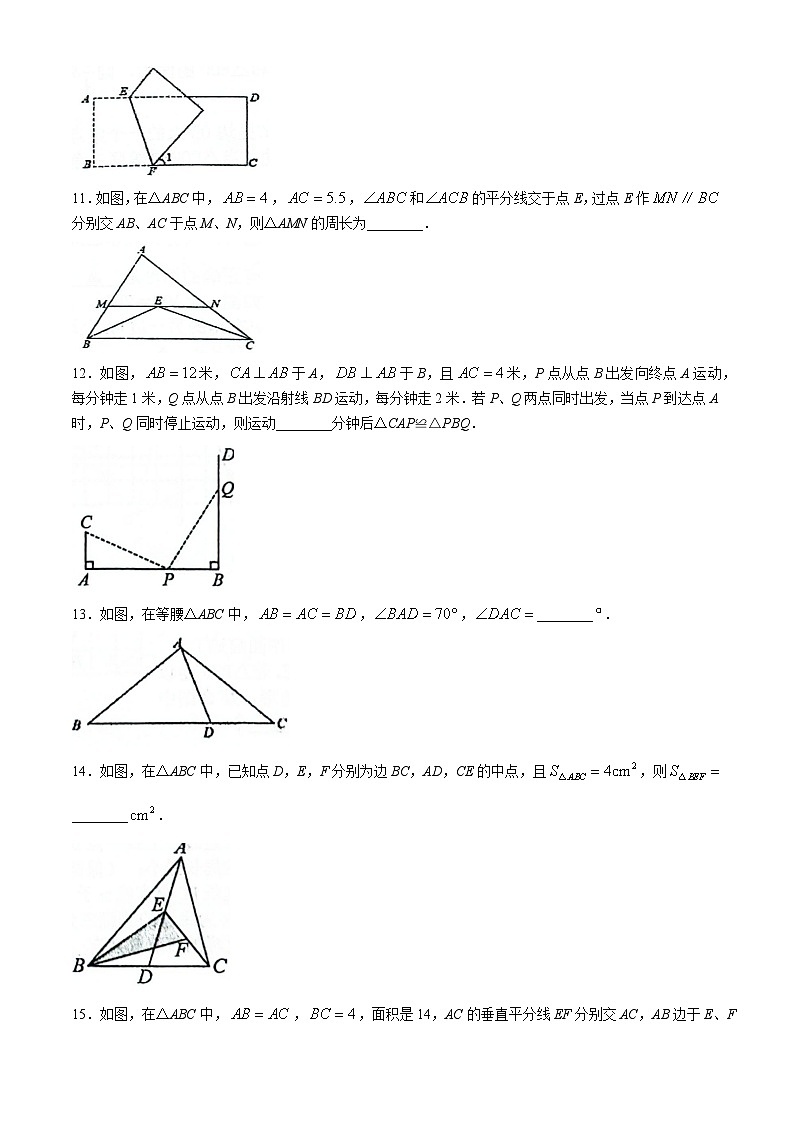
11．如图，在△ABC中，，，和的平分线交于点E，过点E作分别交AB、AC于点M、N，则△AMN的周长为________．
12．如图，米，于A，于B，且米，P点从点B出发向终点A运动，每分钟走1米，Q点从点B出发沿射线BD运动，每分钟走2米．若P、Q两点同时出发，当点P到达点A时，P、Q同时停止运动，则运动________分钟后△CAP≌△PBQ．
13．如图，在等腰△ABC中，，，________．
14．如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且，则________．
15．如图，在△ABC中，，，面积是14，AC的垂直平分线EF分别交AC，AB边于E、F点．若点D为BC边的中点，点M为线段EF上一动点，则的最小值为________．
16．如图，在射线OA，OB上分别截取，连接，在、上分别截取，连接，按此规律作下去，若，则________．（用含的代数式表示）
17．如图，在△ABC中，，，D是BC的中点，点E、F分别在边AB、AC上，且，下列结论：①△BED≌△AFD；②；③，分别表示△ABC和△EDF的面积，则；④；所有正确的结论是________．
18．如图，，点C是边OB上的一个定点，点P在角的另一边OA上运动，当△COP是等腰三角形时，________．
三、解答题（共96分，把解答过程写在答题纸相对应的位置上．）
19．（本题8分）如图，在的方格图中，每个小方格都是边长为1个单位的正方形，每个小正方形的顶点叫做格点．已知△ABC的三个顶点在格点上．
（1）画出，使它与△ABC关于直线m对称；
（2）在直线m上找一点D，使得△BCD的周长最小；（保留作图痕迹）
（3）延长BC交直线m于E，若△BEF是以BE为底边的等腰三角形，那么图中这样的格点F共有________个．
20．（本题8分）如图，在△ABC中，．
（1）用无刻度直尺和圆规完成下列作图（不写作法，保留画图痕迹）；
①作△ABC的高CD；
②作的平分线交AC于点E，交CD于点F；
（2）结合（1）中作图，求证：．
21．（本题8分）如图，在四边形ABCD中，，，，，垂足为E．
（1）求证：△ABD≌△ECB；
（2）若，求的度数．
22．（本题8分）如图，已知点D，E分别是△ABC的边BA和BC延长线上的点，作的平分线AF，若．
（1）求证：△ABC是等腰三角形；
（2）作的平分线交AF于点G，若，求的度数．
23．（本题10分）如图，在△ABC中，，EF垂直平分AC，交AC于点F，交BC于点E，且．
（1）若，求的度数；
（2）若△ABC周长26cm，，求DC长．
24．（本题10分）如图，在△ABC中，BD是高，点D是AC边的中点，点E在BC边的延长线上，ED的延长线交AB于点F，且，若．
（1）求证：△ABC是等边三角形；
（2）请判断线段AD与CE的大小关系，并说明理由．
25．（本题10分）在△ABC中，，BE平分，于D，，点H是BC边的中点，连接DH，交BE于点G，连接CG．
（1）求证：；
（2）求的度数．
26．（本题10分）如图①，在Rt△ABC中，，，，，现有一动点P，从点A出发，沿着三角形的边运动，回到点A停止，速度为3cm/s，设运动时间为ts．
图① 图②
（1）如图①，当________时，△APC的面积等于△ABC面积的一半；
（2）如图②，在△DEF中，，，，．在△ABC的边上，若另外有一个动点Q，与点P同时从点A出发，沿着边运动，回到点A停止．在两点运动过程中的某一时刻，恰好△APQ与△DEF全等，求点Q的运动速度．
27．（本题12分）我们把两个面积相等但不全等的三角形叫做偏等积三角形．
【初步尝试】
（1）如图1，△ABD与△ACD是偏等积三角形，，，且线段AD的长度为正整数，则AD的长度为________；
图1
【理解探究】
（2）如图2，已知△ABC为直角三角形，，以AB，AC为边向外作正方形ABDE，正方形ACFG，连接EG．求证：△ABC与△AEG为偏等积三角形；
图2
（3）如图3，将△ABC分别以AB，BC，AC为边向外作正方形ABDE，正方形BCFG，正方形ACMN，连接DG，FM，NE，则图中有________组偏等积三角形；
图3
【综合运用】
（4）如图4，四边形ABED是一片绿色花园，△ACB、△DCE是等腰直角三角形，，已知，△ACD的面积为．计划修建一条经过点C的笔直的小路CF，点F在BE边上，FC的延长线经过AD的中点G．若小路每米造价600元，请计算修建小路的总造价．
图4
28．（本题12分）在△ABC中，，．若点D在的平分线所在的直线上．
（1）如图1，当点D在△ABC的外部时，过点D作于E，作交AC的延长线于F，且．
图1
①求证：点D在BC的垂直平分线上；
②________；
（2）如图2，当点D在线段BC上时，若，BE平分，交AC于点E，交AD与点F，过点F作，交BC于点G．
图2
①________；
②若，求GC的长度；
（3）如图3，过点A的直线，若，，点D到△ABC三边所在直线的距离相等，则点D到直线l的距离是________．
图3
答 案
一、选择题
1-4：CBDD5-8：DAAC
二、填空
9．110．11．9.512．4
13．14．115．716．
17．①②③18．或或
三、解答
19．
（3）3
20．解：（1）如图，
（2）证明：∵，
∴，
∴，
∵，
∴，
∵，
∴，
∵，
∴．
21．（1）证明：∵，
∴．
∵，，
∴，
在△ABD和△ECB中，
∴△ABD≌△ECB（AAS）；
（2）解：∵△ABD≌△ECB，
∴，
∵，
∴，
又∵，
∴，
∴．
22．（1）证明：∵AF平分，
∴，
∵，
∴，，
∴，
∴△ABC是等腰三角形；
（2）解：∵，，
∴，
∴，
∴，
∵CG平分，
∴
∵，
∴
23．（1）∵，，EF垂直平分AC，
∴，
∴，
∵，
∴
∴
（2）∵△ABC周长26cm，，
∴，
∴，
即，
∴，
∴．
24．（1）证明：∵，点D是AC边的中点，
∴BD垂直平分AC，
∴，
∵，
∴，
∵，
∴，
∴△ABC是等边三角形；
（2）解：，理由如下：
∵△ABC是等边三角形，
∴，
∵，，
∴，
∴，
∵点D是AC边的中点，
∴，
∴．
25．（1）证明：∵，BE平分，
∴，
∴．
易证△ADC≌△FDB，
∴，
∴；
（2）解：∵，
∴，
∵，
∴△BCD是等腰直角三角形，
∴，
∵BE平分，
∴，
∵，点H是BC边的中点，
∴，
∴，
∴，
∴．
26．（1）或；
（2）设点Q的运动速度为acm/s，
∵△APQ与△DEF全等，，
∴，或，，
当P在AC上，点Q在AB上时，
若，，
∴，
∴，
若，，
∴，
∴，
当点P在AB上，点Q在AC时，
若，，
∴，
∴，
若，，
∴，
∴，
综上所述：点Q的运动速度为或或或．
27．（1）3
（2）△ACD与△BCE是偏等积三角形，
理由：如图3，∵
图3
∴，
∵，
∴，
∴，
∵，，
∴△ACD与△BCE不全等，
作于点F，交DC的延长线于点G，则，
∵，
∴，
在△ACG和△BCF中，
∴△ACG≌△BCF（AAS），
∴，
∴，
∴△ACD与△BCE面积相等，
∴△ACD与△BCE是偏等积三角形；
（3）答案为：6．
（4）由（2）同理得，，
图3
过点A作，交CG的延长线于M，
∴，
∵点G为AD的中点，
∴，
∵，
∴△AGM≌△DGC（AAS），
∴，
∵，
∴，
∵，
∴，
∵，，
∴△MAC≌△ECB（SAS），
∴，
∵，
∴，
∴，
∴，
∵，
∴，
∴修建小路的总造价为（元）．
28（1）①如图1，
图1
证明：连接BD，CD，
∵AD平分，
，，
∴，，
∵，
∴△BED≌△CFD（SAS），
∴，
∴点D在BC的垂直平分线上；
②1；
（2）如图2，
图2
①，
②；
（3）点D到l的距离是2或6．