2025届江西省婺源县九年级数学第一学期开学联考模拟试题【含答案】

这是一份2025届江西省婺源县九年级数学第一学期开学联考模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）甲、乙两位射击运动员的10次射击练习成绩的折线统计图如图所示，则下列关于甲、乙这10次射击成绩的说法中正确的是（ ）
A．甲的成绩相对稳定，其方差小B．乙的成绩相对稳定，其方差小
C．甲的成绩相对稳定，其方差大D．乙的成绩相对稳定，其方差大
2、（4分）若无解，则m的值是（ ）
A．3B．﹣3C．﹣2D．2
3、（4分）下列图形是中心对称图形但不是轴对称图形的是（ ）
A．菱形B．矩形C．正三角形D．平行四边形
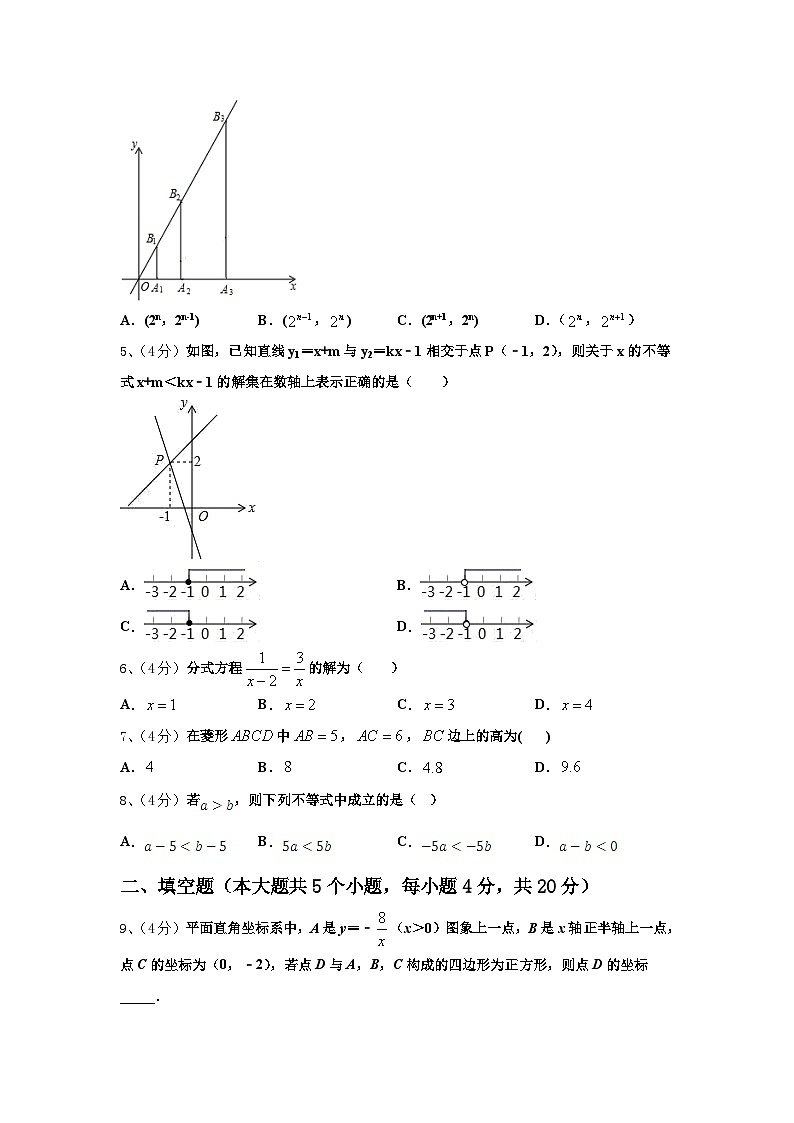
4、（4分）如图，过点作轴的垂线，交直线于点；点与点关于直线对称；过点作轴的垂线，交直线于点；点与点关于直线对称；过点作轴的垂线，交直线于点；按此规律作下去，则点的坐标为
A．(2n，2n-1)B．(，)C．(2n+1，2n)D．（，）
5、（4分）如图，已知直线y1＝x+m与y2＝kx﹣1相交于点P（﹣1，2），则关于x的不等式x+m＜kx﹣1的解集在数轴上表示正确的是（ ）
A．B．
C．D．
6、（4分）分式方程的解为（ ）
A．B．C．D．
7、（4分）在菱形中，，边上的高为( )
A．B．C．D．
8、（4分）若，则下列不等式中成立的是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）平面直角坐标系中，A是y＝﹣（x＞0）图象上一点，B是x轴正半轴上一点，点C的坐标为（0，﹣2），若点D与A，B，C构成的四边形为正方形，则点D的坐标_____．
10、（4分）如图，已知两点A（6，3），B（6，0），以原点O为位似中心，相似比为1：3把线段AB缩小，则点A的对应点坐标是_________
（2，1）或（-2，-1）
11、（4分）一组数据：的方差是__________．
12、（4分）如图，把Rt△ABC(∠ABC＝90°)沿着射线BC方向平移得到Rt△DEF，AB＝8，BE＝5，则四边形ACFD的面积是________．
13、（4分） 若10个数的平均数是3，方差是4，现将这10个数都扩大2倍，则这组新数据的方差是_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）解不等式组，并将不等式组的解集在下面的数轴上表示出来：．
15、（8分）解答题．
某校学生积极为地震灾区捐款奉献爱心．小颖随机抽查其中30名学生的捐款情况如下：（单位：元）2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、1．
（1）这30名学生捐款的最大值、最小值、极差、平均数各是多少？
（2）将30名学生捐款额分成下面5组，请你完成频数统计表：
（3）根据上表，作出频数分布直方图．
16、（8分）为缓解“停车难”的问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图，按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图计算CE．（精确到0.1m）
（下列数据提供参考：20°＝0.3420，20°＝0.9397，20°＝0.3640）
17、（10分）在正方形AMFN中，以AM为BC边上的高作等边三角形ABC，将AB绕点A逆时针旋转90°至点D，D点恰好落在NF上，连接BD，AC与BD交于点E，连接CD，
(1)如图1，求证：△AMC≌△AND；
(2)如图1，若DF=，求AE的长；
(3)如图2,将△CDF绕点D顺时针旋转（）,点C,F的对应点分别为、，连接、，点G是的中点,连接AG，试探索是否为定值，若是定值，则求出该值；若不是，请说明理由.
18、（10分）（1）在图中以正方形的格点为顶点，画一个三角形，使三角形的边长分别为、2、；
（2）求此三角形的面积及最长边上的高.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）约分：_______.
20、（4分）如图是一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②′，…依此类推，若正方形①的边长为64m，则正方形⑨的边长为________cm．
21、（4分）如图，在△ABC中，∠CAB＝65°，在同一平面内，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′∥AB，则∠B′AB等于_____．
22、（4分）等腰三角形的一个外角为100︒，则这个等腰三角形的顶角为_________.
23、（4分）如图，平面直角坐标系中，经过点B(﹣4，0)的直线y＝kx+b与直线y＝mx+2相交于点A(，-1)，则不等式mx+2＜kx+b＜0的解集为____．
二、解答题（本大题共3个小题，共30分）
24、（8分）某商店经销一种双肩包，已知这种双肩包的成本价为每个30元．市场调查发现，这种双肩包每天的销售量y（单位:个）与销售单价x（单位:元）有如下关系：y=－x+60（30≤x≤60）．
设这种双肩包每天的销售利润为w元．
（1）求w与x之间的函数解析式；
（2）这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
（3）如果物价部门规定这种双肩包的销售单价不高于48元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元？
25、（10分）为进一步提升企业产品竞争力，某企业加大了科研经费的投入，2016年该企业投入科研经费5000万元就，2018年投入科研经费7200万元，假设该企业这两年投入科研经费的年平均增长率相同．
（1）求这两年该企业投入科研经费的年平均增长率；
（2）若该企业科研经费的投入还将保持相同的年平均增长率，请你预算2019年该企业投入科研经费多少万元．
26、（12分）某加工厂购进甲、乙两种原料,若甲原料的单价为元千克,乙原料的单价为元千克.现该工厂预计用不多于万元且不少于万元的资金购进这两种原料共千克.
(l)若需购进甲原料千克,请求出的取值范围；
(2)经加工后:甲原料加工的产品,利润率为；每一千克乙原料加工的产品售价为元.则应该怎样安排进货,才能使销售的利润最大？
(3)在(2)的条件下,为了促销,公司决定每售出一千克乙原料加工的产品,返还顾客现金元,而甲原料加工的产品售价不变,要使所有进货方案获利相同,求的值
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
结合图形，乙的成绩波动比较小，则波动大的方差就小.
【详解】
从图看出：乙选手的成绩波动较小，说明它的成绩较稳定的，甲的波动较大，则其方差大.
故选：.
此题考查了方差的意义.方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定.
2、D
【解析】
方程两边同乘以x-3可得m+1-x=0，因无解，可得x=3，代入得m=2，故选D.
3、D
【解析】
根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．
【详解】
解：A、菱形是中心对称图形，也是轴对称图形，故本选项错误；
B、矩形是中心对称图形，也是轴对称图形，故本选项错误；
C、正三角形不是中心对称图形，是轴对称图形，故本选项错误；
D、平行四边形是中心对称图形但不是轴对称图形，故本选项正确．
故选：D．
本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
4、B
【解析】
先根据题意求出点A2的坐标，再根据点A2的坐标求出B2的坐标，以此类推总结规律便可求出点的坐标．
【详解】
∵
∴
∵过点作轴的垂线，交直线于点
∴
∵
∴
∵过点作轴的垂线，交直线于点
∴
∵点与点关于直线对称
∴
以此类推便可求得点An的坐标为，点Bn的坐标为
故答案为：B．
本题考查了坐标点的规律题，掌握坐标点的规律、轴对称的性质是解题的关键．
5、D
【解析】
利用函数图象,找出直线y=x+m在直线y=kx-1的下方所对应的自变量的范围即可
【详解】
解析
根据图象得,当x1b．故本选项错误；
C、在不等式的两边同时乘以-1，不等号的方向发生改变，即-1a2．故本选项错误.
本题主要考查了不等式的基本性质．在解答不等式的问题时，应密切关注符号的方向问题．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4，﹣2）或（2，﹣4）或（2﹣2，2﹣2）．
【解析】
首先依据题意画图图形，对于图1和图2依据正方形的对称性可得到点D的坐标，对于图3可证明△AEC≌△BFA，从而可得到AE=BF，然后由反比例函数的解析式可求得点A的坐标，然后可得到点D的坐标．
【详解】
如图1所示：当CD为对角线时．
∵OC＝2，AB＝CD＝4，
∴D（4，﹣2）．
如图2所示：
∵OC＝2，BD＝AC＝4，
∴D（2，﹣4）．
如图3所示：过点A作AE⊥y轴，BF⊥AE，则△AEC≌△BFA．
∴AE＝BF．
设点A的横纵坐标互为相反数，
∴A（2，﹣2）
∴D（2﹣2，2﹣2）．
综上所述，点D的坐标为（4，﹣2）或（2，﹣4）或（2﹣2，2﹣2）．
故答案为：（4，﹣2）或（2，﹣4）或（2﹣2，2﹣2）．
本题主要考查的是正方形的性质，反比例函数的性质，依据题意画出复合题意得图形是解题的关键．
10、（2，1）或（-2，-1）
【解析】
如图所示：
∵A（6，3），B（6，0）两点，以坐标原点O为位似中心，相似比为，
∴A′、A″的坐标分别是A′（2，1），A″（（﹣2，﹣1）．
故答案为（2，1）或（﹣2，﹣1）．
11、.
【解析】
根据方差的公式进行解答即可.
【详解】
解：==2019，
==0.
故答案为：0.
本题考查了方差的计算.
12、40
【解析】
根据平移的性质可得CF=BE=5，然后根据平行四边形的面积公式即可解答.
【详解】
由平移的性质可得：CF=BE=5,
∵AB⊥BF，
∴四边形ACFD的面积为：AB·CF=8×5=40，
故答案为40.
本题考查了平移的性质和平行四边形面积公式，掌握平移的性质和平行四边形面积公式是解题的关键.
13、1
【解析】
根据方差的性质可知，数据中的每个数据都扩大2倍，则方差扩大4倍，即可得出答案．
【详解】
解：∵将这组数据中的每个数据都扩大2倍，所得到的一组数据的方差将扩大4倍，
∴新数据的方差是4×4＝1，
故答案为：1．
本题考查了方差：一般地设有n个数据，x1，x2，…xn，若每个数据都扩大相同的倍数后，方差则变为这个倍数的平方倍．
三、解答题（本大题共5个小题，共48分）
14、，将不等式组的解集在数轴上表示见解析.
【解析】
分别解两个不等式得两个不等式的解集，然后根据确定不等式组解集的方法确定解集，最后利用数轴表示其解集．
【详解】
由（1）可得
由（2）可得
∴原不等式组解集为
本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
15、 (1) 最大值为1，最小值为2，极差为48，平均数为17.7元．(2)填表见解析；（3）补图见解析.
【解析】
分析：（1）根据给出的数据以及极差、平均数的计算方法直接计算即可解答．
（2）分别找出各组的人数填表即可解答．
（3）根据频数分布表画出频数分布直方图即可解答．
详解：（1）这30名学生捐款的最大值为1，
最小值为2，
极差为1﹣2=48，
平均数为
（2+5+35+8+5+10+15+20+15+5+45+10+2+8+20+30+40+10+15+15+30+15+8+25+25+30+15+8+10+1）÷30=17.7元．
（2）填表如下：
．
（3）画图如下：
点睛：本题主要考查极差、平均数的定义以及画频数分布直方图的能力，正确画图是关键．
16、限高应标3.0．
【解析】
由图得：ÐA＝ÐDCE＝20º
∵AB＝10，在Rt△ABD中，＝，
∴BD＝10×0.3640＝3.64
∴DC＝BD－BC＝3.64－0.5＝3.14
∵在Rt△DEC中，＝，
∴CE＝3.14×0.9397≈3.0
答：限高应标3.0．
这是一题用利用三角函数解决的实际问题，关键在于构造直角三角形Rt△ABD和Rt△DEC.
17、（1）见解析；（2）AE＝；（3）（3），理由见解析.
【解析】
（1）运用四边形AMFN是正方形得到判断△AMC,△AND是Rt△，进一步说明△ABC是等边三角形，在结合旋转的性质，即可证明.
（2）过E作EG⊥AB于G,在BC找一点H，连接DH,使BH=HD，设AG＝，则AE= GE=，得到△GBE是等腰直角三角形和∠DHF=30°，再结合直角三角形的性质，判定Rt△AMC≌Rt△AND，最后通过计算求得AE的长；
（3）延长F1G到M,延长BA交的延长线于N,使得，可得≌，从而得到 ，可知∥, 再根据题意证明≌，进一步说明是等腰直角三角形，然后再使用勾股定理求解即可.
【详解】
（1）证明：∵四边形AMFN是正方形，
∴AM=AN ∠AMC=∠N=90°
∴△AMC,△AND是Rt△
∵△ABC是等边三角形
∴AB=AC
∵旋转后AB=AD
∴AC=AD
∴Rt△AMC≌Rt△AND(HL)
（2）过E作EG⊥AB于G,在BC找一点H，连接DH,使BH=HD，
设AG＝
则AE= GE=
易得△GBE是等腰直角三角形
∴BG=EG＝
∴AB=BC=
易得∠DHF=30°
∴HD=2DF= ，HF=
∴BF=BH+HF=
∵Rt△AMC≌Rt△AND(HL)
∴易得CF=DF=
∴BC=BF-CF=
∴
∴
∴AE＝
（3）；
理由：如图2中,延长F1G到M,延长BA交的延长线于N,使得,则≌,
∴ ,
∴∥,
∴
∵
∴
∴,
∵
∴≌（SAS）
∴
∴
∴是等腰直角三角形
∴
∴
∴
本题考查正方形的性质、三角形全等、以及勾股定理等知识点，综合性强，难度较大，但解答的关键是正确做出辅助线.
18、（1）三角形画对 （2）三角形面积是5 高是
【解析】
试题分析：（1）根据勾股定理画出三角形即可；（2）求出三角形的面积，再由三角形的面积公式即可得出结论.
试题解析：
（1）如图，△ABC即为所求.
（2），
最长边的高为：.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据分式的基本性质，分子分母同时除以公因式3ab即可。
【详解】
解：分子分母同时除以公因式3ab，得：
故答案为：
本题考查了分式的基本性质的应用，分式的约分找到分子分母的公因式是关键，是基础题。
20、4
【解析】
第一个正方形的边长为64cm，则第二个正方形的边长为64×cm，第三个正方形的边长为64×（）2cm，依此类推，通过找规律求解．
【详解】
根据题意：第一个正方形的边长为64cm；
第二个正方形的边长为：64×=32cm；
第三个正方形的边长为：64×（）2cm，
…
此后，每一个正方形的边长是上一个正方形的边长的 ，
所以第9个正方形的边长为64×（）9-1=4cm，
故答案为4
本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．
21、50°
【解析】
由平行线的性质可求得∠C/CA的度数，然后由旋转的性质得到AC=AC/，然后依据三角形的性质可知∠AC/C的度数，依据三角形的内角和定理可求得∠CAC/的度数，从而得到∠BAB/的度数.
解：∵CC/∥AB，
∴∠C/CA=∠CAB=65°，
∵由旋转的性质可知：AC=AC/,
∴∠ACC/=∠AC/C=65°.
∴∠CAC/=180°-65°-65°=50°.
∴∠BAB/=50°.
22、12.
【解析】
因为题中没有指明该外角是顶角的外角还是底角的外角，所以应该分两种情况进行讨论．
【详解】
解：当100°的角是顶角的外角时，顶角的度数为180°-100°=80°；
当100°的角是底角的外角时，底角的度数为180°-100°=80°，所以顶角的度数为180°-2×80°=20°；
∴顶角的度数为80°或20°．
故答案为80°或20°．
本题考查等腰三角形的性质，三角形内角和定理及三角形外角性质等知识；分情况进行讨论是解答问题的关键．
23、﹣4＜x＜﹣
【解析】
根据函数的图像，可知不等式mx+2＜kx+b＜0的解集就是y=mx+2在函数y=kx+b的下面，且它们的值小于0的解集是﹣4＜x＜﹣.
故答案为﹣4＜x＜﹣.
二、解答题（本大题共3个小题，共30分）
24、（1）w=－x2+90x－1800；（2）当x=45时，w有最大值，最大值是225（3）该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为40元
【解析】试题分析：（1）根据销售利润=单个利润×销售量，列出式子整理后即可得；
（2）由（1）中的函数解析式，利用二次函数的性质即可得；
（3）将w=200代入（1）中的函数解析式，解方程后进行讨论即可得.
试题解析：（1）w=（x﹣30）•y=（﹣x+60）（x﹣30）=﹣x2+30x+60x﹣1800=﹣x2+90x﹣1800，
w与x之间的函数解析式w=﹣x2+90x﹣1800；
（2）根据题意得：w=﹣x2+90x﹣1800=﹣（x﹣45）2+225，
∵﹣1＜0，
当x=45时，w有最大值，最大值是225；
（3）当w=200时，﹣x2+90x﹣1800=200，
解得x1=40，x2=50，
∵50＞42，x2=50不符合题意，舍去，
答：该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为40元．
25、（1）这两年该企业投入科研经费的年平均增长率为20%；（2）2019年该企业投入科研经费8640万元．
【解析】
（1）设这两年该企业投入科研经费的年平均增长率为x，根据2016年及2018年投入科研经费，即可得出关于x的一元二次方程，解之取其正值即可得出结论；
（2）根据2019年投入科研经费＝2018年投入科研经费×（1+增长率），即可求出结论．
【详解】
解：（1）设这两年该企业投入科研经费的年平均增长率为x，
根据题意得：5000（1+x）2＝7200，
解得：x1＝0.2＝20%，x2＝﹣2.2（不合题意，舍去）．
答：这两年该企业投入科研经费的年平均增长率为20%．
（2）7200×（1+20%）＝8640（万元）．
答：2019年该企业投入科研经费8640万元．
本题考查了一元二次方程的应用，解题的关键是：（1）找准等量关系，正确列出一元二次方程；（2）根据2019年投入科研经费＝2018年投入科研经费×（1＋增长率），列式计算．
26、（1）；（2）购进甲原料7千克，乙原料13千克时，获得利润最大；（3）；
【解析】
（1）根据题意，由该工厂预计用不多于万元且不少于万元的资金购进这两种原料，列出不等式组，求出x的范围即可；
（2）根据题意，可求出甲、乙每千克的利润，比较大小，在（1）的前提下，选出利润最大的进货方案即可；
（3）根据题意，要使所有进货方案获利相同，列出方程，求出m的值即可.
【详解】
解：（1）需购进甲原料千克，则乙原料为（20-x）千克，则
，解得：，
∴x的取值范围为：；
（2）根据题意，有
甲原料每千克的利润为：
乙原料每千克的利润为：元，
由（1）知，，则进货方案有4种，分别为：
①购进甲7千克，乙13千克；
②购进甲8千克，乙12千克；
③购进甲9千克，乙11千克；
④购进甲10千克，乙10千克；
∵，
∴购进乙原料越多，利润越大，
∴当购进甲原料7千克，乙原料13千克时，获得利润最大，
最大利润为：元；
（3）由（2）知，要使所有进货方案获利相同，则有

解得：；
∴当时，所有进货方案的获得利润相同；
本题考查了二元一次方程组的应用、以及解一元一次不等式组，解题的关键是：找准等量关系，正确列出不等式组和方程，并求解；
题号
一
二
三
四
五
总分
得分