2025届泉州市重点中学数学九上开学考试模拟试题【含答案】

这是一份2025届泉州市重点中学数学九上开学考试模拟试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
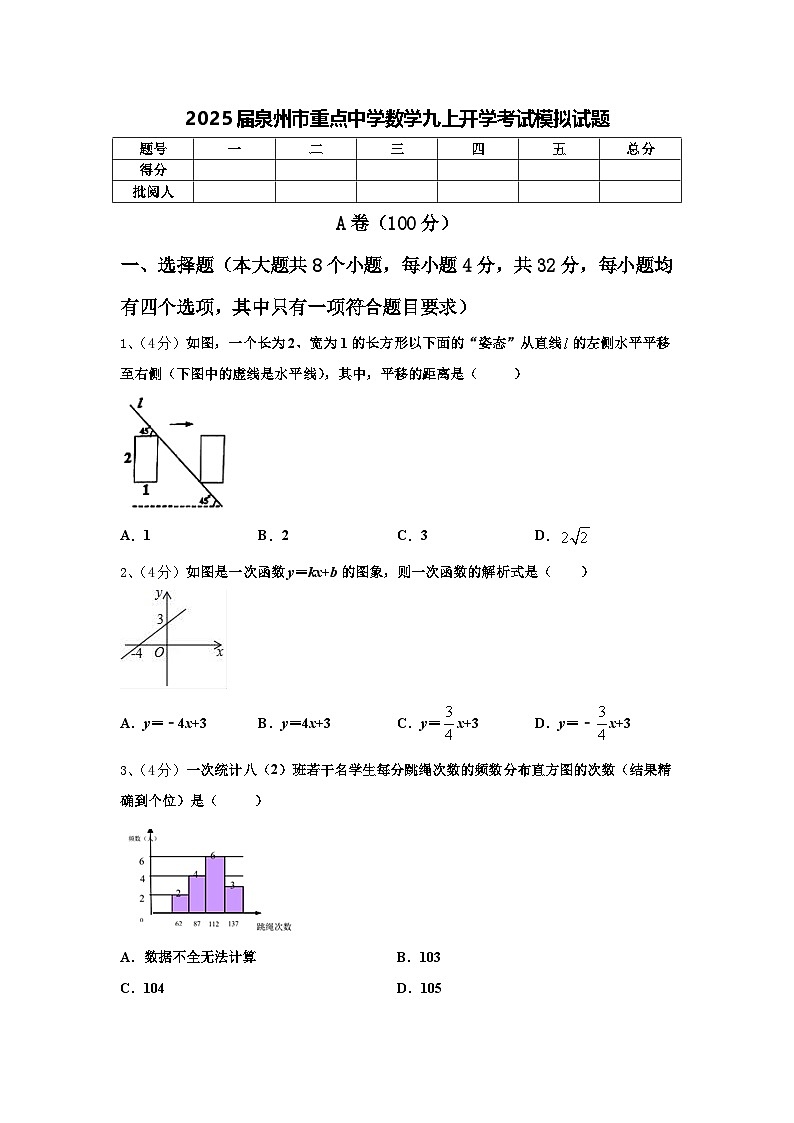
1、（4分）如图，一个长为2、宽为1的长方形以下面的“姿态”从直线的左侧水平平移至右侧（下图中的虚线是水平线），其中，平移的距离是（ ）
A．1B．2C．3D．
2、（4分）如图是一次函数y＝kx+b的图象，则一次函数的解析式是（ ）
A．y＝﹣4x+3B．y＝4x+3C．y＝x+3D．y＝﹣x+3
3、（4分）一次统计八（2）班若干名学生每分跳绳次数的频数分布直方图的次数（结果精确到个位）是（ ）
A．数据不全无法计算B．103
C．104D．105
4、（4分）正方形ABCD的边长为2，以AD为边作等边△ADE，则点E到BC的距离是（ ）
A．2+B．2-C．2+，2-D．4-
5、（4分）与可以合并的二次根式是（ ）
A．B．C．D．
6、（4分）关于x的一元二次方程有两个不相等的实数根，则实数m的取值范围为（ ）
A．B．C．D．
7、（4分）下列四组线段中，可以构成直角三角形的是（ ）
A．4，5，6B．2，3，4C．1.5，2，2.5D．1，，3
8、（4分）已知△ABC的三边分别是a，b，c，且满足|a-2|++（c-4）2=0，则以a，b，c为边可构成（ ）
A．以c为斜边的直角三角形B．以a为斜边的直角三角形
C．以b为斜边的直角三角形D．有一个内角为的直角三角形
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，Rt△ABC中，∠ACB=90°，点D为斜边AB的中点，CD=6cm，则AB的长为 cm．
10、（4分）点P的坐标为，则点P到x轴的距离是________，点P到y轴的距离是________．
11、（4分）将代入反比例函数中，所得函数值记为，又将代入函数中，所得函数值记为，再将代入函数中，所得函数值记为，如此继续下去，则________.
12、（4分）先化简：，再对a选一个你喜欢的值代入，求代数式的值．
13、（4分）如图，直线y1＝－x＋a与直线y2＝bx－4相交于点P(1，－3)，则不等式－x＋a≥bx－4的解集是___________．
三、解答题（本大题共5个小题，共48分）
14、（12分）直线与轴轴分别交于点A和点B，M是OB上一点，若将△ABM沿AM折叠，点B恰好落在轴上的点B′处，试求出直线AM的解析式.
15、（8分）已知与成正比例，且当时，，则当时，求的值.
16、（8分）某经销商从市场得知如下信息：
他计划用4万元资金一次性购进这两种品牌手表共100块，设该经销商购进A品牌手表x块，这两种品牌手表全部销售完后获得利润为y元．
（1）试写出y与x之间的函数关系式；
（2）若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案；
（3）选择哪种进货方案，该经销商可获利最大；最大利润是多少元.
17、（10分）我国古代数学著作《九章算术》中的一个问题．原文是：今有池方一丈，葭生其中央，出水尺．引葭赴岸，适与岸齐问水深、葭长各几何译文大意是：如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池边的中点，它的顶端恰好到达池边的水面．问水的深度与这根芦苇的长度分别是多少？
18、（10分）如图，抛物线y＝﹣x2﹣x+4与x轴交于A，B两点(A在B的左侧)，与y轴交于点C．
(1)求点A，点B的坐标；
(2)求△ABC的面积；
(3)P为第二象限抛物线上的一个动点，求△ACP面积的最大值．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知关于的方程的解是正数，则的取值范围是__________．
20、（4分）分解因式：__________．
21、（4分）若一个三角形的三边长为6，8，10，则最长边上的高是____________.
22、（4分）如图一个圆柱，底圆周长10cm，高4cm，一只蚂蚁沿外壁爬行，要从A点爬到B点，则最少要爬行_______cm .
23、（4分）在Rt△ABC中，∠C＝90°，若a=6，b=8，则c=________．
二、解答题（本大题共3个小题，共30分）
24、（8分）完成下列运算
（1）计算：
（2）计算：
（3）计算：
25、（10分）如图：矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1．
（1）判断△BEC的形状，并说明理由？
（2）判断四边形EFPH是什么特殊四边形？并证明你的判断；
（3）求四边形EFPH的面积．
26、（12分）在平面直角坐标系xOy中，点P到封闭图形F的“极差距离”D(P，W)定义如下：任取图形W上一点Q，记PQ长度的最大值为M，最小值为m(若P与Q重合，则PQ＝0)，则“极差距离”D(P，W)＝M﹣m.如图，正方形ABCD的对角线交点恰与原点O重合，点A的坐标为(2，2)
(1)点O到线段AB的“极差距离”D(O，AB)＝______.点K(5，2)到线段AB的“极差距离”D(K，AB)＝______.
(2)记正方形ABCD为图形W，点P在x轴上，且“极差距离”D(P，W)＝2，求直线AP的解析式.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据平移的性质即可解答.
【详解】
如图连接，根据平行线的性质得到∠1=∠2，
如图，平移的距离的长度
故选C.
此题考查平移的性质，解题关键在于利用平移的性质求解.
2、C
【解析】
将点（﹣4，0）、（0，1）坐标代入一次函数y＝kx+b求出k、b即可．
【详解】
解：设一次函数解析式为：y＝kx+b，
根据题意，将点A（﹣4，0）和点B（0，1）代入得：
，
解得：，
∴一次函数解析式为：y＝x+1．
故选C．
本题考查的是待定系数法求一次函数的解析式，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
3、C
【解析】
根据频数分布直方图可知本次随机抽查的学生人数为：2+4+6+3=15（人）；然后取每一小组中间的数值近似地作为该组内每位学生的每分钟跳绳次数，再用加权平均数求解即可.
【详解】
解：根据频数分布直方图可知本次随机抽查的学生人数为：2+4+6+3=15（人）；所以这若干名学生每分钟跳绳次数的平均数=（62×2+87×4+112×6+137×2）÷15≈103.67≈104，
故选C.
本题考查学生读取频数分布直方图的能力和利用统计图获取信息的能力.对此类问题，必须认真观察题目所给的统计图并认真的思考分析，才能作出正确的判断，从而解决问题.
4、C
【解析】
由等边三角形的性质可得点E到AD上的距离为，分两种情况可求点E到BC的距离．
【详解】
解：∵等边△ADE的边长为2
∴点E到AD上的距离EG为，
当△ADE在正方形外面，
∴点E到BC的距离=2+
当△ADE在正方形里面
∴点E到BC的距离=2-
故选：C．
本题考查了正方形的性质，等边三角形的性质，熟练运用正方形的性质是本题的关键．
5、C
【解析】
先对各个选项中的二次根式化简为最简二次根式（被开方数中不含分母且被开方数中不含有开得尽方的因数或因式），再在其中找的同类二次根式（化成最简二次根式后的被开方数相同,这样的二次根式叫做同类二次根式.）.
【详解】
A. 为最简二次根式，且与不是同类二次根式，故错误；
B. = -3，与不是同类二次根式，故错误；
C. ，与是同类二次根式，故正确；
D. 为最简二次根式，且与不是同类二次根式，故错误.
故选C.
本题考查二次根式的加减，能将各个选项中根式化简为最简二次根式，并能找对同类二次根式是本题的关键.
6、B
【解析】
根据方程有两个不等的实数根，故△＞0，得不等式解答即可.
【详解】
试题分析：由已知得△＞0，即（﹣3）2﹣4m＞0，
解得m＜．
故选B．
此题考查了一元二次方程根的判别式.
7、C
【解析】
由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
【详解】
解：A、42+52=41≠62，不可以构成直角三角形，故A选项错误；
B、22+32=13≠42，不可以构成直角三角形，故B选项错误；
C、1.52+22=6.25=2.52，可以构成直角三角形，故C选项正确；
D、，不可以构成直角三角形，故D选项错误．
故选：C．
本题考查勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
8、B
【解析】
利用非负数的性质求得a、b、c的数值，利用勾股定理的逆定理判定三角形的形状即可．
【详解】
解：由题意可得：a=，b=2，c=4，
∵22+42=20，()2＝20，
即b2+c2=a2，
所以△ABC是以a为斜边的直角三角形．
故选B．
本题考查了非负数的性质和勾股定理的逆定理，根据非负数的性质求得a、b、c的值是解决此题的关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1.
【解析】
试题分析：∵在Rt△ABC中，∠ACB=90°，D是AB的中点，
∴线段CD是斜边AB上的中线；
又∵CD=6cm，
∴AB=2CD=1cm．
故答案是：1．
考点：直角三角形斜边上的中线．
10、2 1
【解析】
根据在平面直角坐标系中，任何一点到x轴的距离等于这一点纵坐标的绝对值，到y轴的距离等于这一点横坐标的绝对值，即可解答本题．
【详解】
解：点P的坐标为，则点P到x轴的距离是2，点P到y轴的距离是1．
故答案为2；1．
本题考查在平面直角坐标系中，点到坐标轴的距离，比较简单．
11、2
【解析】
可依次求出y的值，寻找y值的变化规律，根据规律确定的值.
【详解】
解：将代入反比例函数中得；
将代入函数得；
将代入函数得；
将代入函数得
由以上计算可知：y的值每三次重复一下
故y的值在重复670次后又计算了2次，所以
故答案为：2
本题属于反比例函数的求值规律题，找准函数值的变化规律是解题的关键.
12、；3
【解析】
原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，将a=3代入计算即可求出值．
【详解】
原式．
∵且
∴当a=3时，原式=
此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
13、x≤1.
【解析】
观察函数图象得到当x