2025届山东省滨州惠民县联考九年级数学第一学期开学教学质量检测试题【含答案】

这是一份2025届山东省滨州惠民县联考九年级数学第一学期开学教学质量检测试题【含答案】，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）在平面直角坐标系中，点（﹣2，﹣a2﹣3）一定在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2、（4分）下表是校女子排球队12名队员的年龄分布：
则关于这12名队员的年龄的说法正确的是（ ）
A．中位数是14B．中位数是14.5C．众数是15D．众数是5
3、（4分）不等式 的解集为（ ）.
A．B．C．D．
4、（4分）关于x的不等式组的解集为x＜3，那么m的取值范围为（ ）
A．m=3B．m＞3C．m＜3D．m≥3
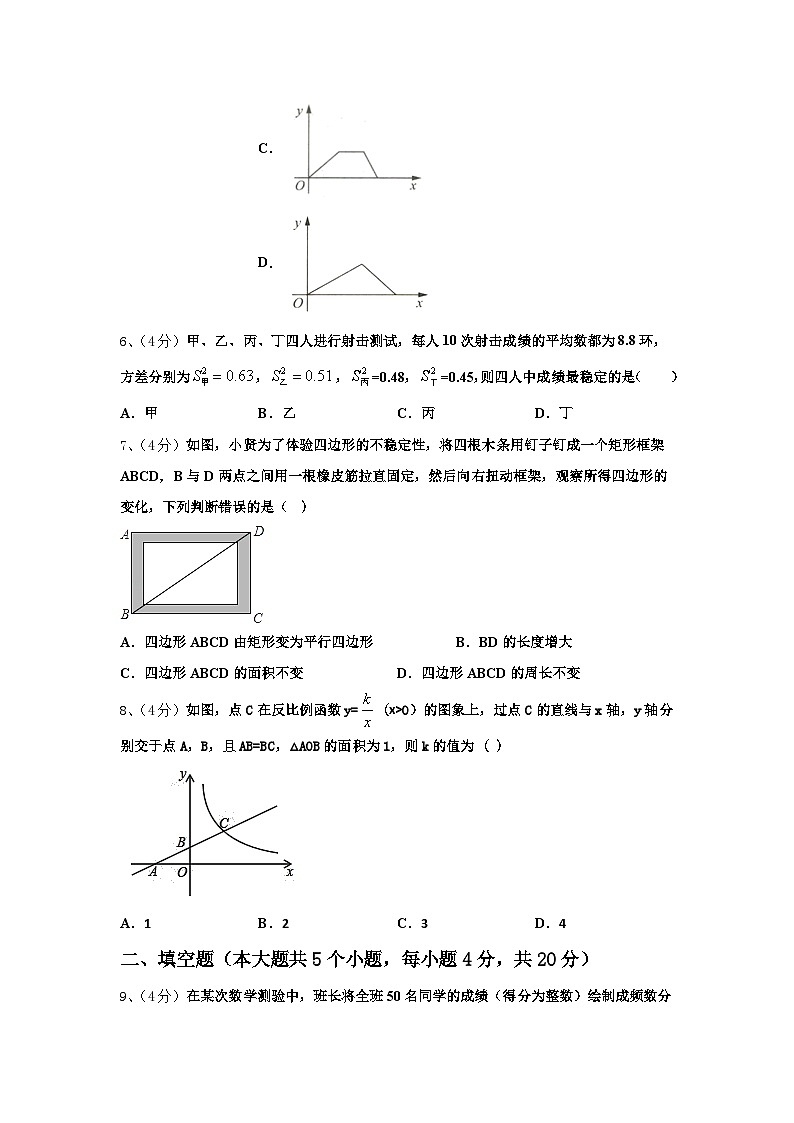
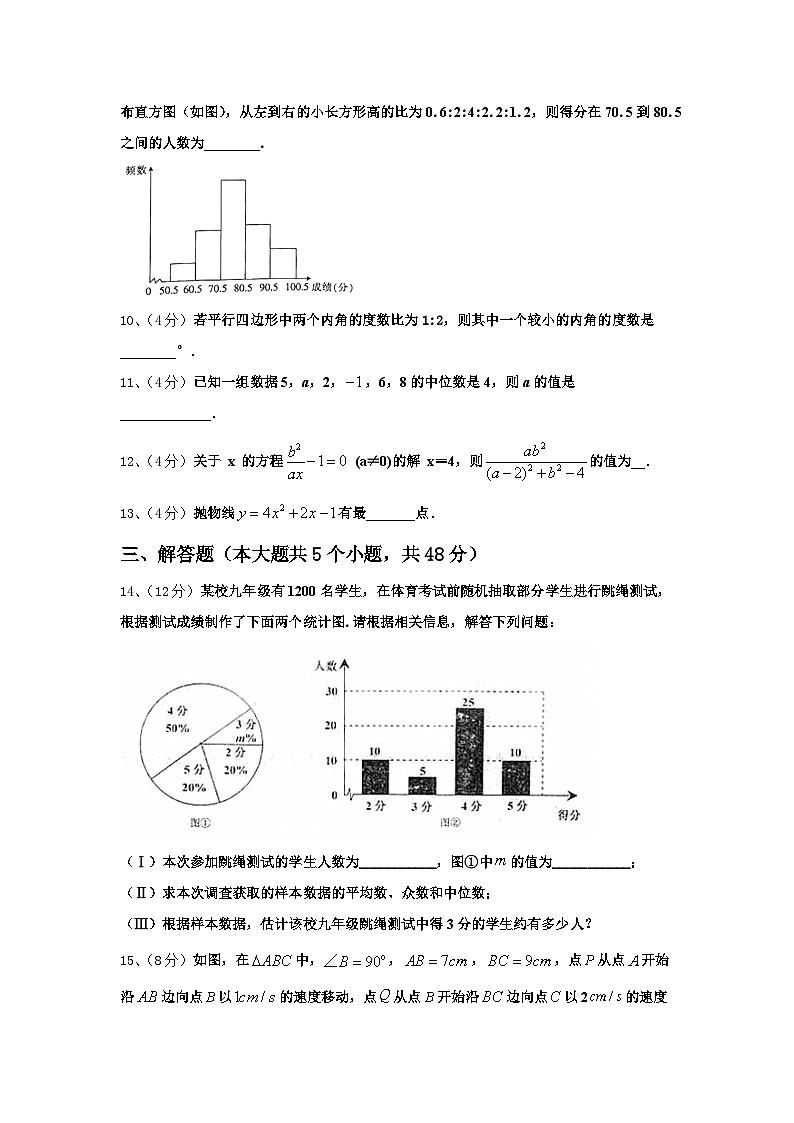
5、（4分）小华的爷爷每天坚持体育锻炼，某天他慢跑从家到中山公园，打了一会儿太极拳后坐公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图像是（ ）.
A．B．C．D．
6、（4分）甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都为8.8环，方差分别为，，=0.48，=0.45，则四人中成绩最稳定的是（ ）
A．甲B．乙C．丙D．丁
7、（4分）如图，小贤为了体验四边形的不稳定性，将四根木条用钉子钉成一个矩形框架ABCD，B与D两点之间用一根橡皮筋拉直固定，然后向右扭动框架，观察所得四边形的变化，下列判断错误的是（ ）
A．四边形ABCD由矩形变为平行四边形 B．BD的长度增大
C．四边形ABCD的面积不变D．四边形ABCD的周长不变
8、（4分）如图，点C在反比例函数y=（x>0）的图象上，过点C的直线与x轴，y轴分别交于点A，B，且AB=BC，△AOB的面积为1，则k的值为（ ）
A．1B．2C．3D．4
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）在某次数学测验中，班长将全班50名同学的成绩（得分为整数）绘制成频数分布直方图（如图），从左到右的小长方形高的比为0.6:2:4:2.2:1.2，则得分在70.5到80.5之间的人数为________.
10、（4分）若平行四边形中两个内角的度数比为1:2，则其中一个较小的内角的度数是________°．
11、（4分）已知一组数据5，a，2，，6，8的中位数是4，则a的值是_____________．
12、（4分）关于 x 的方程 (a≠0)的解 x＝4，则的值为__．
13、（4分）抛物线有最_______点．
三、解答题（本大题共5个小题，共48分）
14、（12分）某校九年级有1200名学生，在体育考试前随机抽取部分学生进行跳绳测试，根据测试成绩制作了下面两个统计图.请根据相关信息，解答下列问题：
（Ⅰ）本次参加跳绳测试的学生人数为___________，图①中的值为___________；
（Ⅱ）求本次调查获取的样本数据的平均数、众数和中位数；
（Ⅲ）根据样本数据，估计该校九年级跳绳测试中得3分的学生约有多少人？
15、（8分）如图，在中，，，，点从点开始沿边向点以的速度移动，点从点开始沿边向点以2的速度移动．
（1）如果点，分别从点，同时出发，那么几秒后，的面积等于6？
（2）如果点，分别从点，同时出发，那么几秒后，的长度等于7？
16、（8分）为了解某校八年级学生每周平均课外阅读时间的情况,随机抽查了该校八年级部分学生,对其每周平均课外阅读时间进行统计,根据统计数据绘制成如图的两幅尚不完整的统计图:
（1）本次共抽取了多少人?并请将图1的条形图补充完整；
（2）这组数据的众数是________；求出这组数据的平均数；
（3）若全校有1500人,请你估计每周平均课外阅读时间为3小时的学生多少人?
17、（10分）如图，平面直角坐标系中，已知点，若对于平面内一点C，当是以AB为腰的等腰三角形时，称点C时线段AB的“等长点”．
请判断点，点是否是线段AB的“等长点”，并说明理由；
若点是线段AB的“等长点”，且，求m和n的值．
18、（10分）（本小题满分12分）
直线y=x+6和x轴，y轴分别交于点E，F，点A是线段EF上一动点（不与点E重合），过点A作x轴垂线，垂足是点B，以AB为边向右作长方形ABCD，AB：BC=3：1．
（1）当点A与点F重合时（图1），求证：四边形ADBE是平行四边形，并求直线DE的表达式；
（2）当点A不与点F重合时（图2），四边形ADBE仍然是平行四边形？说明理由，此时你还能求出直线DE的表达式吗？若能，请你出来．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）有一个质地均匀的正方体，其六个面上分别写着直角梯形、等腰梯形、矩形、正方形、菱形、平行四边形，投掷这个正方体后，向上的一面的图形是对角线相等的图形的概率是_______；
20、（4分）如图，正方形ABCD中，，点E、F分别在边AD和边BC上，且，动点P、Q分别从A、C两点同时出发，点P自A→F→B方向运动，点Q自C→D→E→C方向运动若点P、Q的运动速度分别为1cm/s，3cm/s，设运动时间为，当A 、C、P、Q四点为顶点的四边形是平行四边形时则t= ________________
21、（4分）在实数范围内定义一种运算“﹡”，其规则为a﹡b＝a2﹣b2，根据这个规则，方程（x+1）﹡3＝0的解为_____．
22、（4分）在大课间活动中，体育老师对甲、乙两名同学每人进行10次立定跳远测试，他们的平均成绩相同，方差分别是，则甲、乙两名同学成绩更稳定的是 ．
23、（4分）如图，在四边形中，交于E,若，则的长是_____________
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在平面直角坐标系中，，顶点；直线．
（1）点的坐标是______，对角线与的交点的坐标是______．
（2）①过点的直线的解析式是______．
②过点的直线的解析式是______．
③判断①、②中两条直线的位置关系是______．
（3）当直线平分的面积时，的值是______．
（4）一次函数的图像______（填“能”或“不能”）平分的面积．
25、（10分）如图，的一个外角为，求，，的度数.
26、（12分）如图，中，，点从点出发沿射线移动，同时，点从点出发沿线段的延长线移动，已知点、的移动速度相同，与直线相交于点.
（1）如图1，当点在线段上时，过点作的平行线交于点，连接、，求证：点是的中点；
（2）如图2，过点作直线的垂线，垂足为，当点、在移动过程中，线段、、有何数量关系？请直接写出你的结论： .
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据直角坐标系的坐标特点即可判断.
【详解】
解：∵a2+3≥3＞0，
∴﹣a2﹣3＜0，
∴点（﹣2，﹣a2﹣3）一定在第三象限．
故选C．
此题主要考查直角坐标系点的特点，解题的关键是熟知各象限坐标特点.
2、C
【解析】
根据众数、中位数的定义逐一计算即可判断．
【详解】
观察图表可知：人数最多的是5人，年龄是1岁，故众数是1．
共12人，中位数是第6，7个人平均年龄，因而中位数是1．
故选：．
本题主要考查众数、中位数，熟练掌握众数、中位数的定义是解题的关键．
3、B
【解析】
先移项，再系数化为1即可得到不等式的解集.
【详解】
解：移项得：
合并同类项得：
系数化为1得：
故选：B
本题考查了一元一次不等式的解法，熟练掌握计算法则是关键，当两边除以负数时，要注意不等号的方向要改变.
4、D
【解析】
解不等式组得：，
∵不等式组的解集为x＜3
∴m的范围为m≥3，
故选D．
5、C
【解析】
根据在每段中，离家的距离随时间的变化情况即可进行判断．
【详解】
图象应分三个阶段，第一阶段：慢步到离家较远的绿岛公园，在这个阶段，离家的距离随时间的增大而增大；第二阶段：打了一会儿太极拳，这一阶段离家的距离不随时间的变化而改变。故D错误；第三阶段：搭公交车回家，这一阶段，离家的距离随时间的增大而减小，故A错误，并且这段的速度大于第一阶段的速度，则B错误.
故选：C.
本题考查函数图象，解题的关键是由题意将图象分为三个阶段进行求解.
6、D
【解析】
根据方差的意义进行判断．
【详解】
解：∵＜＜＜
∴四人中成绩最稳定的是丁．
故选：D．
本题考查了方差：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
7、C
【解析】
试题分析：由题意可知，当向右扭动框架时，BD可伸长，故BD的长度变大，四边形ABCD由矩形变为平行四边形 ，因为四条边的长度不变，所以四边形ABCD的周长不变.原来矩形ABCD的面积等于BC乘以AB，变化后平行四边形ABCD的面积等于底乘以高，即BC乘以BC边上的高，BC边上的高小于AB，所以四边形ABCD的面积变小了，故A,B,D说法正确，C说法错误.故正确的选项是C.
考点：1.四边形面积计算；2.四边形的不稳定性.
8、D
【解析】
【分析】过点C作轴，设点 ，则 得到点C的坐标，根据的面积为1，得到的关系式，即可求出的值.
【解答】过点C作轴，
设点 ，则
得到点C的坐标为：
的面积为1，
即

故选D.
【点评】考查反比例函数图象上点的坐标特征，掌握待定系数法是解题的关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、20
【解析】
所有小长方形高的比为0.6：2：4：2.2：1.2，可以求出得分在70.5到80.5之间的人数的小长方形的高占总高的比，进而求出得分在70.5到80.5之间的人数．
【详解】
解：人
故答案为：20
考查频数分布直方图的制作特点以及反映数据之间的关系，理解各个小长方形的高表示的实际意义，用所占比去乘以总人数就得出相应的人数．
10、60°
【解析】
根据平行四边形的性质得出，推出，根据，求出即可.
【详解】
四边形是平行四边形，
，
，
，
.
故答案为：.
本题考查了平行线的性质和平行四边形的性质的应用，能熟练地运用性质进行计算是解此题的关键，题目比较典型，难度不大.
11、1
【解析】
先确定从小到大排列后a的位置，再根据中位数的定义解答即可．
【详解】
解：根据题意，a的位置按照从小到大的排列只能是：﹣1，2，a，5，6，8；
根据中位数是4，得：，解得：a=1．
故答案为：1．
本题考查的是中位数的定义，属于基本题型，熟知中位数的概念是解题的关键．
12、4
【解析】
将x=4代入已知方程求得b =4a，然后将其代入所以的代数式求值．
【详解】
∵关于x的方程 (a≠0)的解x=4，
∴，
∴b=4a，
∴= ，
故答案是：4.
此题考查分式方程的解，分式的化简求值，解题关键在于求得b =4a
13、低
【解析】
因为：，根据抛物线的开口向上可得答案．
【详解】
解：因为：，所以根据抛物线的开口向上，抛物线图像有最低点．
故答案：低．
本题考查的符号决定抛物线的图像的开口方向，掌握抛物线的图像特点是解题关键．
三、解答题（本大题共5个小题，共48分）
14、（I）50，1；（Ⅱ）3.7，4，4（Ⅲ）120人
【解析】
（I）把条形图中的各组人数相加即可求得参加跳绳测试的学生人数，利用百分比的意义求得m即可；
（Ⅱ）利用加权平均数公式求得平均数，然后利用众数、中位数定义求解；
（Ⅲ）利用总人数乘以对应的百分比即可求解．
【详解】
解：（Ⅰ）本次参加跳绳的学生人数是1+5+25+1=50（人），
m=10×=1．
故答案是：50，1；
（Ⅱ）平均数是：（1×2+5×3+25×4+1×5）=3.7（分），
∵在这组数据中，4出现了25次，出现次数最多；
∴这组样本数据的众数是：4；
∵将这组样本数据自小到大的顺序排列，其中处于最中间位置的两个数都是4，有
∴这组样本数据的中位数是：4；
（Ⅲ）∵在50名学生中跳绳测试得3分的学生人数比例为1%，
∴估计该校该校九年级跳绳测试中得3分的学生有1200×1%=120（人）．
答：该校九年级跳绳测试中得3分的学生有120人．
本题考查的是条形统计图的综合运用，还考查了加权平均数、中位数和众数以及用样本估计总体．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
15、（1）出发1秒后，的面积等于6；（2）出发0秒或秒后，的长度等于7．
【解析】
（1）设秒后，的面积等于6，根据路程=速度×时间，即可用x表示出AP、BQ和BP的长，然后根据三角形的面积公式列一元二次方程，并解方程即可；
（2）设秒后，的长度等于7，根据路程=速度×时间，即可用y表示出AP、BQ和BP的长，利用勾股定理列一元二次方程，并解方程即可．
【详解】
解： （1）设秒后，的面积等于6，
∵点从点开始沿边向点以的速度移动，点从点开始沿边向点以2的速度移动
∴，
∴
则有
∴（此时2×6=12＞BC，故舍去）
答：出发1秒后，的面积等于6
（2）设秒后，的长度等于7
∵点从点开始沿边向点以的速度移动，点从点开始沿边向点以2的速度移动
∴，
∴
解得
答：出发0秒或秒后，的长度等于7．
此题考查的是一元二次方程的应用，掌握几何问题中的等量关系和行程问题公式是解决此题的关键．
16、（1）60人，图见解析；（2）众数是3，平均数是2.75；（3）500人.
【解析】
（1）根据统计图中的数据可以求得本次共抽取了学生多少人，阅读3小时的学生有多少人，从而可以将条形统计图补充完整；
（2）根据统计图中的数据可以求得众数和平均数；
（3）根据统计图中的数据可以求得课外阅读时间为3小时的学生有多少人．
【详解】
解：（1）由图2知阅读时间为2小时的扇形图圆形角为90°，即阅读时间为2小时的概率为，再根据图1可知阅读2小时的人数为15人，所以本次共抽取了15÷ =60名学生，阅读3小时的学生有：60-10-15-10-5=20（名），
补充完整的条形统计图如下图所示；
（2）由条形统计图可得，
这组数据的众数是3，
这组数据的平均数是：；
（3）1500× =500（人），
答：课外阅读时间为3小时的学生有500人．
本题考查条形统计图、扇形统计图、用样本估计总体、加权平均数、众数，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
17、是线段AB的“等长点”，不是线段AB的“等长点”，理由见解析；，或，．
【解析】
先求出AB的长与B点坐标，再根据线段AB的“等长点”的定义判断即可；
分两种情况讨论，利用对称性和垂直的性质即可求出m，n．
【详解】
点，，
，，，
．
点，
，
，
是线段AB的“等长点”，
点，
，，
，，
不是线段AB的“等长点”；
如图，
在中，，，
，
．
分两种情况：
当点D在y轴左侧时，
，
，
点是线段AB的“等长点”，
，
，
，；
当点D在y轴右侧时，
，
，
，
点是线段AB的“等长点”，
，
．
综上所述，，或，．
本题考查了新定义，锐角三角函数，直角三角形的性质，等腰三角形的性质，坐标与图形性质解的关键是理解新定义，解的关键是画出图形，是一道中等难度的中考常考题．
18、（1）；（2）四边形ADBE仍然是平行四边形；.
【解析】
试题分析：对于直线y=x+6，分别令x与y为0求出y与x的值，确定出E与F坐标，
（1）当A与F重合时，根据F坐标确定出A坐标，进而确定出AB的长，由AB与BC的比值求出BC的长，确定出AD=BE，而AD与BE平行，利用一组对边平行且相等的四边形为平行四边形得到四边形AEBD为平行四边形；根据AB与BC的长确定出D坐标，设直线DE解析式为y=kx+b，将D与E坐标代入求出k与b的值，即可确定出直线DE解析式；
（2）当点A不与点F重合时，四边形ADBE仍然是平行四边形，理由为：根据直线y=x+6解析式设出A坐标，进而表示出AB的长，根据A与B横坐标相同确定出B坐标，进而表示出EB的长，发现EB=AD，而EB与AD平行，利用一组对边平行且相等的四边形为平行四边形得到四边形AEBD为平行四边形；根据BC的长求出OC的长，表示出D坐标，设直线DE解析式为y=k1x+b1，将D与E坐标代入求出k1与b1的值，即可确定出直线DE解析式．
试题解析：对于直线y=x+6，
令x=0，得到y=6；令y=0，得到x=﹣8，即E（﹣8，0），F（0，6），
（1）当点A与点F重合时，A（0，6），即AB=6，
∵AB：BC=2：1，
∴BC=8，
∴AD=BE=8，
又∵AD∥BE，
∴四边形ADBE是平行四边形；
∴D（8，6），
设直线DE解析式为y=kx+b（k、b为常数且k≠0），
将D（8，6），E（﹣8，0）代入得：，
解得：b=2，k=．
则直线DE解析式为y=x+2；
（2）四边形ADBE仍然是平行四边形，理由为：
设点A（m，m+6）即AB=m+6，OB=﹣m，即B（m，0），
∴BE=m+8，
又∵AB：BC=2：1，
∴BC=m+8，
∴AD=m+8，
∴BE=AD，
又∵BE∥AD，
∴四边形ADBE仍然是平行四边形；
又∵BC=m+8，
∴OC=2m+8，
∴D（2m+8，m+6），
设直线DE解析式为y=k1x+b1（k1、b1为常数且k1≠0），
将D与E坐标代入得：，
解得：k1=，b1=2，
则直线DE解析式为y=x+2．
考点：一次函数综合题．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
【分析】先求出总的情况和对角线相等的情况，再根据概率公式可求得.
【详解】因为，出现的图形共有6种情况，对角线相等的有（等腰梯形，正方形，矩形）3这情况，所以，P（对角线相等）=
故答案为：
【点睛】本题考核知识点：概率.解题关键点：掌握概率的求法.
20、3s或6s
【解析】
根据两点速度和运动路径可知，点Q在EC上、点P在AF上或和点P在BC上时、点Q在AD上时，A、C、P、Q四点为顶点的四边形是平行四边形．根据平行四边形性质构造方程即可．
【详解】
由P、Q速度和运动方向可知，当Q运动EC上，P在AF上运动时，
若EQ=FP，A、C、P、Q四点为顶点的四边形是平行四边形
∴3t-7=5-t
∴t=3
当P、Q分别在BC、AD上时
若QD=BP，形A、C、P、Q四点为顶点的四边形是平行四边形
此时Q点已经完成第一周
∴4-[3（t-4）-4]=t-5+1
∴t=6
故答案为：3s或6s．
本题考查了正方形的性质，平行四边形的判定和性质，动点问题的分类讨论和三角形全等有关知识．解答时注意分析两个动点的相对位置关系．
21、x=2、-4
【解析】
先根据新定义得到，再移项得，然后利用直接开平方法求解.
【详解】
(x+1)﹡3＝0，
，
，
，
所以、.
故答案为：、.
本题考查了解一元二次方程-直接开平方法：如果方程化成的形式，那么可得，如果方程能化成（）的形式，那么.
22、乙
【解析】
试题分析：方差就是和中心偏离的程度，用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）在样本容量相同的情况下，方差越小，说明数据的波动越小，越稳定．因此，
∵，∴甲、乙两名同学成绩更稳定的是乙．
23、
【解析】
过点A作AM⊥BD于M,先证明△AEM≌△BEC，得出AM=BC，BE=ME，再根据得出三角形ADM是等腰直角三角形，从而得出AM=BC,结合已知和勾股定理得出DB和BC的长即可
【详解】
过点A作AM⊥BD于M,则
∵
∴
∵EA=EC，
∴
∴AM=BC，BE=ME
∵则设EB=2k,ED=5k
∴EM=2k,DM=3k
∵,
∴AM=DM=BC=3k,BM=4k
则AB=5k=5，k=1
∴DB=7,BC=3
∵
∴DC=
故答案为：
本题考查了全等三角形的判定与性质，等腰直角三角形的性质与判定，以及勾股定理，熟练掌握相关知识是解题的关键
二、解答题（本大题共3个小题，共30分）
24、（1）；（2）①；②； ③相交；（3）1； （1）不能．
【解析】
（1）根据平行四边形的性质以及A、B两点的坐标可得CD∥AB∥x轴，CD=AB=1，再利用平移的性质得出点C的坐标；根据平行四边形的对角线互相平分得出E是BD的中点，再利用线段的中点坐标公式求出点E的坐标；
（2）①将点A（1，1）代入y=kx-3k+1，求出k的值即可；
②将点B（5，1）代入y=kx-3k+1，求出k的值即可；
③将两直线的解析式联立组成方程组：，解得：，即可判断①、②中两条直线的位置关系是相交；
（3）当直线y=kx-3k+1平分▱ABCD的面积时，直线y=kx-3k+1经过▱ABCD对角线的交点E（2，0），将E点坐标代入y=kx-3k+1，求出k的值即可；
（1）将x=2代入y=kx-2k+1，求出y=1≠0，即直线y=kx-2k+1不经过▱ABCD对角线的交点E（2，0），即可判断一次函数y=kx-2k+1的图象不能平分▱ABCD的面积．
【详解】
解：（1）∵四边形ABCD是平行四边形，A（1，1），B（5，1），
∴CD∥AB∥x轴，CD=AB=1，
∵D（-1，-1），
∴点C的坐标是（-1+1，-1），即（3，-1），
∵E是对角线AC与BD的交点，
∴E是BD的中点，
∵B（5，1），D（-1，-1），
∴点E的坐标是（2，0）．
故答案为（3，-1），（2，0）；
（2）①将点A（1，1）代入y=kx-3k+1，
得1=k-3k+1，解得，
则所求的解析式是．
故答案为：；
②将点B（5，1）代入y=kx-3k+1，
得1=k-3k+1，解得，
则所求的解析式是；
故答案为：；
③由，解得
∴①、②中两条直线的位置关系是相交，交点是（3，1）．
故答案为：相交；
（3）∵直线y=kx-3k+1平分▱ABCD的面积时，
∴直线y=kx-3k+1经过▱ABCD对角线的交点E（2，0），
∴0=2k-3k+1，解得k=1．
故答案为：1；
（1）∵x=2时，y=kx-2k+1=1≠0，
∴直线y=kx-2k+1不经过▱ABCD对角线的交点E（2，0），
∴一次函数y=kx-2k+1的图象不能平分▱ABCD的面积．
故答案为：不能．
本题考查了两条直线的交点问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解．也考查了平行四边形的性质，一次函数的性质，一次函数图象上点的坐标特征，线段的中点坐标公式等知识．
25、，，
【解析】
利用已知可先求出∠BCD=110°，根据平行四边形的性质知，平行四边形的对角相等以及邻角互补来求∠A，∠B，∠D的度数．
【详解】
∵四边形ABCD是平行四边形，
∴∠A=∠BCD，∠B=∠D，AB//CD，
∵▱ABCD的一个外角为38°，
∴∠BCD=142°，
∴∠A=142°，∠B=∠DCE=38°，∴∠D=38°．
本题主要考查了平行四边形的性质，解题的关键是掌握平行四边形对角相等，邻角互补．
26、（1）见解析；（2）或.
【解析】
（1）由题意得出BD=CE，由平行线的性质得出∠DGB=∠ACB，由等腰三角形的性质得出∠B=∠ACB，得出∠B=∠DGB，证出BD=GD=CE，即可得出结论；
（2）由（1）得：BD=GD=CE，由等腰三角形的三线合一性质得出BM=GM，由平行线得出GF=CF，即可得出结论．
【详解】
（1）四边形CDGE是平行四边形．理由如下：
∵D、E移动的速度相同，
∴BD=CE，
∵DG∥AE，
∴∠DGB=∠ACB，
∵AB=AC，
∴∠B=∠ACB，
∴∠B=∠DGB，
∴BD=GD=CE，
又∵DG∥CE，
∴四边形CDGE是平行四边形；
（2）当点D在AB边上时，BM+CF=MF；理由如下：
如图2，
由（1）得：BD=GD=CE，
∵DM⊥BC，
∴BM=GM，
∵DG∥AE，
∴GF=CF，
∴BM+CF=GM+GF=MF．
同理可证，当D点在BA的延长线上时，可证， 如图3，4.
本题考查了等腰三角形的判定与性质、平行四边形的判定与性质；熟练掌握等腰三角形的性质，并能进行推理论证是解决问题的关键．
题号
一
二
三
四
五
总分
得分
年龄（岁）
13
14
15
16
人数（名）
1
4
5
2