广东省汕头市潮阳区铜盂镇2023-2024学年八年级上学期期末数学试题

这是一份广东省汕头市潮阳区铜盂镇2023-2024学年八年级上学期期末数学试题，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

（全卷总共120分，考试用时120分钟）
一、单选题（本大题共10小题，每小题3分，共30分）
1.杨絮，又名大叶杨花絮.据《本草纲目》记载，杨絮具有清热解毒、益肝明目等功效，杨树果实将要成熟时，果实开裂，杨絮四处飞扬，飘在大街上会让人呼吸道不畅，因此，行道树禁止种植杨树，建议种其他树种.据测定，某种杨絮纤维的直径约为0.0000105m，该数据用科学记数法表示为（）
A.B.C.D.
2.已知三角形的两边长分别为5和9，则此三角形的第三边长可能为（）
A.3B.4C.10D.14
3.若分式的值为零，则的值是（）
A.2B.C.D.0
4.下列各式从左到右分解因式正确的是（）
A.B.
C.D.
5.正五边形的内角等于（）度.
A.60B.72C.90D.108
6.下列计算正确的是（）
A.B.C.D.
7.将一副三角板的直角顶点重合，并按如图方式放置，其中，则的度数为（）
A.B.C.D.
8.如图，已知：直线、被所截，交点分别是点、，其中，，点是线段上一点，.则（）
A.B.C.D.
9.如图，在和中，，以下条件不能判定的是（）
A.B.C.D.
10.若数使关于的分式方程的解为非负数，且使关于的不等式组
的解集为，则符合条件的所有整数的个数为（）
A.5B.6C.7D.8
二、填空题（一）（本大题共6小题，每小题3分，共18分）
11.如果分式有意义，那么的取值范围是________.
12.一个机器人从点出发，每前进1米，就向右转体，照这样走下去，如果他恰好能回到点，且所走过的路程最短，则的值等于________.
13.如图，是尺规法作的平分线时保留的痕迹，这样作可使，全等的根据是________.
14.若关于的方程无解.则________.
15.如图，在中，，，交于点，若，则________.
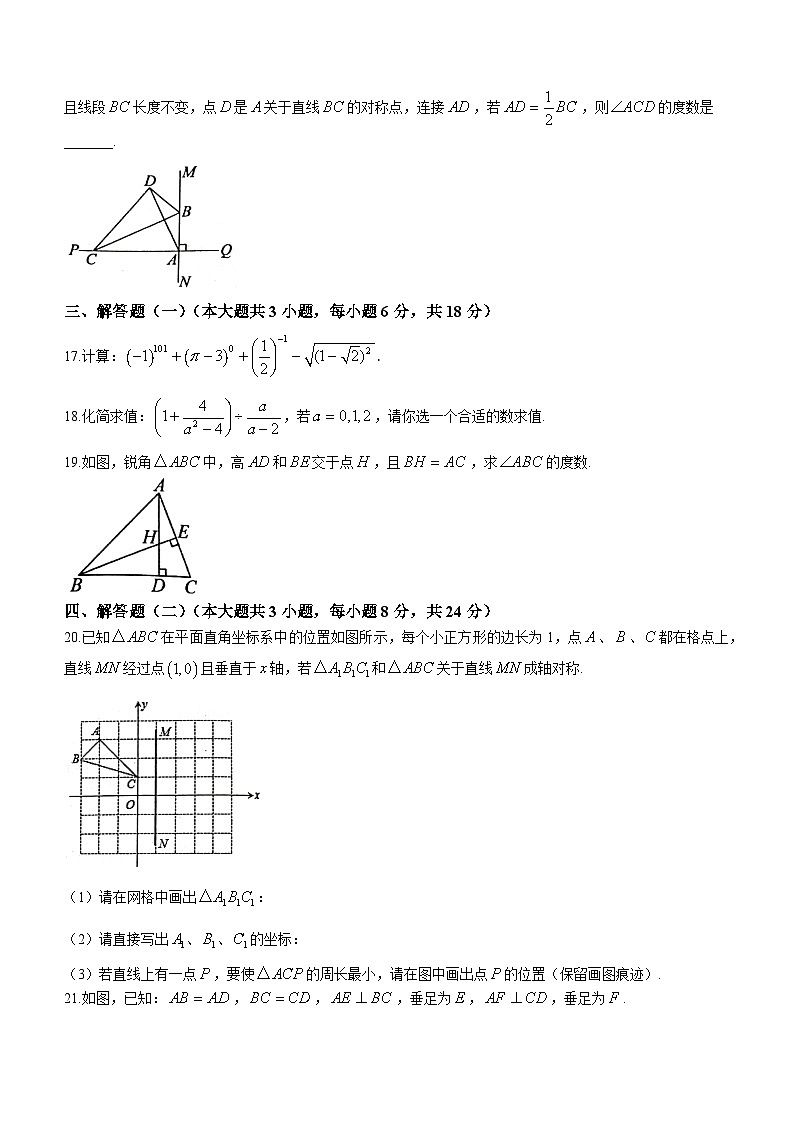
16.如图，直线与直线相交于点，并且互相垂直，点和点分别是直线和上的两个动点，且线段长度不变，点是关于直线的对称点，连接，若，则的度数是_______.
三、解答题（一）（本大题共3小题，每小题6分，共18分）
17.计算：.
18.化简求值：，若，请你选一个合适的数求值.
19.如图，锐角中，高和交于点，且，求的度数.
四、解答题（二）（本大题共3小题，每小题8分，共24分）
20.已知在平面直角坐标系中的位置如图所示，每个小正方形的边长为1，点、、都在格点上，直线经过点且垂直于轴，若和关于直线成轴对称.
（1）请在网格中画出：
（2）请直接写出、、的坐标：
（3）若直线上有一点，要使的周长最小，请在图中画出点的位置（保留画图痕迹）.
21.如图，已知：，，，垂足为，，垂足为.
求证：（1）；
（2）.
22.某玩具商店用2500元购进一批儿童玩具，上市后很快脱销，接着又用4500元购进第二批这种玩具，所购数量是第一批数量的15倍，但每套进价多了10元.
（1）求第一批玩具每套的进价是多少元？
（2）如果这两批玩具每套售价相同，且全部售完后，商店想要获得不低于1750元的利润，那么每套售价至少是多少元？
五、解答题（三）（本大题共3小题，每小题10分，共30分）
23.观察下列等式：
完成下列问题：
（1）________
（2）________（结果用幂表示）.
（3）已知，，求.
24.如图，在中，，，点为内一点，且.
（1）求证：；
（2），为延长线上的一点，且.
①求证：平分；
②若点在上，且，请判断、的数量关系，并给出证明；
25.如图，在平面直角坐标系中，，，且，满足，点，关于轴对称.
图1图2
（1）求，两点坐标：
（2）如图1，点为射线上点右侧一动点，过点作交直线于，连，是否存在点，使？若存在，求点坐标：若不存在，说明理由.
（3）如图2，点为轴正半轴上一动点，点为第一象限内一动点，且，过点作于点.
①若点在的延长线上，求证：平分；
②的值是否发生变化？若不变，求其值，若变化，请说明理由.
2023~2024学年度第一学期八年级期末质量监测数学答案
1.B
【分析】根据科学记数法表示较小的数，一般形式为，其中，为由原数左边起第一个不为零的数字前面的0的个数所决定，进而求解.
【详解】，故选B.
【点睛】本题考查了用科学记数法表示较小的数，一般形式为，其中，正确确定与的值是解题的关键，
2.C
【分析】根据三角形的三边关系确定第三边的取值范围，结合选项解答即可.
【详解】解：设三角形的第三边长为，
则，即，
能作为第三边长，故选：C
【点睛】本题考查的是三角形的三边关系，掌握三角形两边之和大于第三边、三角形的两边差小于第三边是解题的关键.
3.B
【分析】根据分式的值为零的条件：分子等于零，分母不等于零，进行列式求解即可.
【详解】解：由题意可知：，
解得：，故选：B.
【点睛】此题考查了分式的值为零的条件，熟练掌握分式的值为零的条件是解题的关键.
4.D
【分析】根据分解因式进行判断即可.
【详解】解：A、等式右边不是整式积的形式，错误；
B、是整式的乘法运算，错误；
C、等式左边不能分解因式，错误；
D、正确.
故选：D.
【点睛】本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解因式，分解因式要彻底是解题关键。
5.D
【分析】根据多边形内角和公式进行求解即可.
【详解】解：五边形内角和：，
所以，正五边形的内角为：.
故选：D
【点睛】本题考查了多边形内角和公式，正多边形的定义，熟记多边形内角和公式是解题的关键.
6.B
【分析】利用幂的乘方与积的乘方的法则，同底数幂的乘法法则，合并同类项法则对每个选项进行分析，即可得出答案。
【详解】解：A、，则此项错误，不符合题意；
B、，则此项正确，符合题意；
C、，则此项错误，不符合题意；
D、，则此项错误，不符合题意；
故选：B.
【点睛】本题考查了幂的乘方与积的乘方，同底数幂的乘法，合并同类项，熟练掌握幂的乘方与积的乘方的法则，同底数幂的乘法法则，合并同类项法则是解题关键.
7.D
【分析】根据平行线的性质可得，再由三角形外角的性质，即可求解.
【详解】解：如图，与交于点，
根据题意得：，，，，
.
故选D.
【点睛】本题主要考查了平行线的性质，三角形外角的性质，熟练掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.
8.B
【详解】试题解析：，，.，
.
故选B.
考点：平行线的性质
9.D
【分析】本题考查添加条件使三角形全等，涉及三角形全等判定，根据四个选项中的条件，结合已知条件，由三角形全等的判定定理逐项验证即可得到答案.
【详解】解：A、在和中，，，添加，由三角形全等的判定定理SAS即可确定，该选项不符合题意；
B、在和中，，，添加，由三角形全等的判定定理ASA即可确定，该选项不符合题意；
C、在和中，，，添加，由三角形全等的判定定理AAS即可确定，该选项不符合题意；
D、在和中，，，添加，由三角形全等的判定定理SSS、SAS、AAS即可确定无法判断，该选项符合题意；故选：D.
10.C
【分析】根据分式方程的解为非负数求得，根据不等式组的解集为，求得，利用分式的分母不等于0得到，即可得到的取值范围，且，根据整数的意义得到的整数值.
【详解】解分式方程，得，分式方程的解为非负数，
，解得，关于的不等式组，得，
不等式组的解集为，，，，
，且，
整数为：、、0、2、3、4、5，共有7个，故选：C
【点睛】此题考查根据分式方程的解的情况求未知数的取值范围，根据不等式组的解集情况求末知数的取值范围，确定不等式的整数解，正确理解题意并计算是解题的关键.
11.不等于
【分析】直接利用分式的分母不等于0，进而得出答案，
【详解】由题意，得：
，解得：，故答案为：.
【点睛】本题考查了分式有意义的条件，利用分母不能为零得出不等式是解题关键.
12.120
【分析】根据多边形的外角和等于360°，用，所得最小整数就是多边形的边数，然后再求出即可.
【详解】解：根据题意，机器人所走过的路线是正多边形，
边数，走过的路程最短，则最小，最大，最小是3，最大是.
故答案为：120.
【点睛】本题考查了多边形的外角与边数的关系，判断出机器人走过的路线是正多边形并知道边数最少的多边形是三角形是解题的关键.
13..
【分析】根据角平分线的作图方法解答.
【详解】根据角平分线的作法可知，，，又是公共边，
的根据是“SSS”.
故答案为SSS.
【点睛】本题考查了全等三角形的判定，熟悉角平分线的作法，找出相等的条件是解题的关键.
14.3
【分析】先去分母得到整式方程，整理得，由于关于的方程无解，则，即，然后把代入即可求出的值.
【详解】去分母得，整理得，
关于的方程无解.，即，，.
故答案为3.
【点睛】此题考查分式方程的解，解题关键在于利用方程无解进行解答.
15.9
【分析】此题考查了直角三角形两锐角互余，含直角三角形的性质，首先根据直角三角形两锐角互余得到，，然后利用含直角三角形的性质求解即可.解题的关键是熟练掌握直角三角形两锐角互余，含直角三角形的性质.
【详解】解：，，
，，，
，，，，
，.
故答案为：9.
16.或
【分析】分两种情况：当时，取的中点，连接、，当时，取的中点，连接、，根据直角三角形斜边上的中线的性质、等边三角形的判定得出是等边三角形，进而依据轴对称的性质、等腰三角形的性质、三角形外角的定义及性质以及三角形内角和定理进行计算即可得出答案.
【详解】解：如图，当时，取的中点，连接、，
，为的中点，
，
点是关于直线的对称点，
垂直平分，，
，，，
是等边三角形，，，
，，，
，，
；
当时，取的中点，连接、，
同理可得，，
，，，
，
综上所述，的度数是30°或150°，故答案为：30°或150°.
【点睛】本题主要考查了等边三角形的判定与性质、直角三角形的性质、等腰三角形的判定与性质、三角形内角和定理、三角形外角的定义及性质、轴对称的性质等知识点，采用分类讨论的思想是解此题的关键.
17.
【分析】根据整数指数幂的定义、任何非零数的零次幂为1、负整数指数幂的定义、二次根式的运算法化简原式，从而求出答案.
【详解】原式.
【点睛】本题主要考查了整式的运算和整数指数幂，解本题的要点在于熟知各种数幂的计算以及整式的运算法.
18.化简得（5分）取1，并说明不能取0或2得（7分）求出值为
【详解】试题分析：先把所给的分式化成最简分式，然后把代入计算即可.
试题解析：，
因为分母不能为0，所以不能取0和2，所以取，则原式
考点：分式的化简求值
19.的度数为
【分析】先根据三角形全等的判定定理与性质得出，再根据等腰三角形的性质即可得出答案.
【详解】由题意得，
在和中，
是等腰三角形
即的度数为.
【点睛】本题考查了三角形全等的判定定理与性质、等腰三角形的性质等知识点，找出两个全等三角形是解题关键.
20.（1）如图所示，即为所求：
（2）如图所示，、、，
（3）如图所示，点即为所求.
【分析】（1）直接利用轴对称图形的性质得出对应点位置进而得出答案；
（2）直接在坐标系中写出各点坐标即可；
（3）连接，进而得到与交点，即为点.
【详解】（1）如图所示，即为所求；
（2）如图所示，、、，
（3）如图所示，点即为所求.
【点睛】此题主要考查对称轴图形的坐标变换，解题的关键是根据题意正确作出图像再进行求解.
21.详见解析.
【分析】（1）先利用SSS证明，再根据全等三角形的对应角相等即可得出；
（2）根据全等三角形的对应角相等得出，再根据角的平分线上的点到角的两边的距离相等即可得出.
【详解】（1）在与中，
，；
（2），
，
，垂足为，，垂足为，
.
【点睛】本题考查了全等三角形的判定与性质，角平分线的性质，证明出是解题的关键.
22.（1）第一批玩具每套的进价是50元
（2）每套售价至少是70元
【分析】（1）设第一批玩具每套的进价是元，由题意：某玩具商店用2500元购进一批儿童玩具，接着又用4500元购进第二批这种玩具，所购数量是第一批数量的1.5倍，但每套进价多了10元.列出分式方程，解方程即可；
（2）设每套售价是元，由题意：这两批玩具每套售价相同，且全部售完后，商店想要获得不低于1750元利润，列出一元一次不等式，解不等式即可.
【详解】（1）解：设第一批玩具每套的进价是元，
根据题意可得：，
解得：，
经检验，是分式方程的解，且符合题意.
答：第一批玩具每套的进价是50元
（2）解：设每套售价是元，（套），（套），
由题意得：，
解得：，答：每套售价至少是70元.
【点睛】本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出分式方程；（2）找出数量关系，正确列出一元一次不等式.
23.（1）；（2）；（3）76.
【分析】（1）根据规律可得结果；
（2）利用（1）得出的规律先计算即可得出结果；
（3）利用（1）得出的规律变形，再用完全平方公式进行变形，变成只含及的形式，整体代入计算即可得到结果.
【详解】解：（1），
，
由此规律可得：
，
故答案是：；
（2）由（1）的规律可得
.
故答案是：.
（3）已知，，求.
.
故答案是：76.
【点睛】此题考查了多项式乘以多项式，弄清题中的规律是解本题的关键.
24.（1）见解析
（2）①见解析；②，见解析
【分析】（1）如图，延长，交于点，可证，
于是，
由三线合一，得证；
（2）①可求，根据三角形内角和定理及外角知识，
可求，，
进一步求证，结论得证；
②，理由如下，图，连接，得是等边三角形，于是，可证，于是，得.
【详解】（1）证明：如图，延长，交于点，
，，，
.
.
，.
（2）①，，
.
.
.
，即平分.
②，理由如下，
如图，连接，，，
是等边三角形.
.
中，，.
.
.
.
，，.
.
.
【点睛】本题考查等腰三角形性质，全等三角形的判定和性质，等边三角形的判定和性质，三角形的内角和定理；添加辅助线，构造全等三角形是解题的关键.
25.（1），
（2）存在，
（3）①见详解②不变化，2
【分析】（1）由，可得，根据非负数的性质可得，，即可获得答案；
（2）连接，过点作轴于点，首先证明，由可得，再利用轴对称的性质可得，则有，易得，证明，由全等三角形的性质可得，结合，可计算，可获得答案；
（3）过点作于点，首先证明，可得，即可证明平分;
②在上取，证明，可得，即可获得答案.
【详解】（1）解：，
整理可得，
，，
解得，
，
点，关于轴对称，；
（2）连接，过点作轴于点，如下图，点，关于轴对称，
，，，，，
，，，
，
为等腰直角三角形，，
，
，
，，，
，即，
，，
，轴，
，
，
又，，
，
，
，即，
，，
；
（3）①证明：过点作于点，如下图，
，，
又，，
，，
，，平分；
②不变化，在上取，连接，如下图，
，垂直平分，
，，
平分，，，
，，
，，
.
【点睛】本题主要考查了坐标与图形、轴对称的性质、线段垂直平分线的性质、全等三角形的判定与性质、角平分线的性质的知识，解题关键是正确作出辅助线，构造全等三角形.