
河北省保定市莲池区2023-2024学年九年级上学期期末数学试题
展开
这是一份河北省保定市莲池区2023-2024学年九年级上学期期末数学试题,共10页。
注意事项:1.本试卷共8页,总分120分,考试时间120分钟.
2.答题前,考生务必将姓名、准考证号填写在答题卡上相应的位置.
3.所有答案均在答题卡上作答,在本试卷或草稿纸上作答无效.答题前,请仔细阅读答题卡,上的“注意事项”,按照“注意事项”的规定答题.
4.答选择题时,用2B铅笔将答题卡上对应题目的答题标号涂黑;答非选择题时,请在答题卡上对应题目的答题区域内答题.
卷Ⅰ(选择题,共42分)
一、选择题(本大题共16个小题,1~10题,每小题3分;11~16题,每小题2分;共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中,属于二次函数的是()
A.B.C.D.
2.一个正方体截去四分之一,得到如图所示的几何体,其主视图是()
A.B.C.D.
3.一个口袋中有红球、白球共20个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有40次摸到白球.请你估计这个口袋中有()个白球.
A.4B.6C.8D.12
4.用配方法解方程,下列变形正确的是()
A.B.C.D.
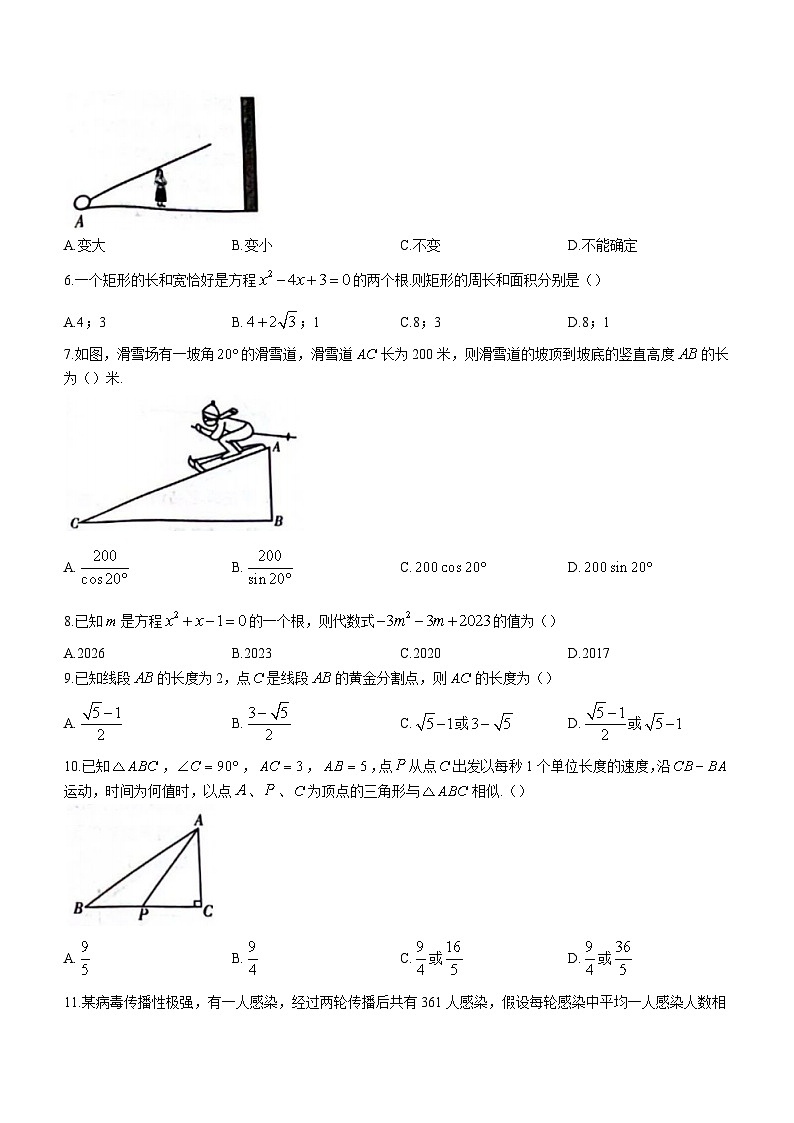
5.如图,在一间黑屋子的地面处有一盏探照灯,当人从灯向墙运动时,他在墙上的影子的大小变化情况是()
A.变大B.变小C.不变D.不能确定
6.一个矩形的长和宽恰好是方程的两个根.则矩形的周长和面积分别是()
A.4;3B.;1C.8;3D.8;1
7.如图,滑雪场有一坡角的滑雪道,滑雪道长为200米,则滑雪道的坡顶到坡底的竖直高度的长为()米.
A.B.C.D.
8.已知是方程的一个根,则代数式的值为()
A.2026B.2023C.2020D.2017
9.已知线段的长度为2,点是线段的黄金分割点,则的长度为()
A.B.C.或D.或
10.已知,,,,点从点出发以每秒1个单位长度的速度,沿运动,时间为何值时,以点、、为顶点的三角形与相似.()
A.B.C.或D.或
11.某病毒传播性极强,有一人感染,经过两轮传播后共有361人感染,假设每轮感染中平均一人感染人数相同,按这样的速度第三轮后共有()人被传染.
A.380B.6859C.7220D.6498
12.如图,在正方形中,是的中点,阴影部分的面积是2,则正方形的边长是()
A.B.C.D.
13.如图,在给定的平行四边形上,作一个菱形,甲、乙二人的做法如下:
甲:分别以、为圆心,长为半径画弧,交于点,交于点,连接,则四边形为菱形;
乙:以为圆心,长为半径画弧,交于点,连接,作的垂直平分线交于点,则四边形为菱形;
根据两人的做法可判断()
A.甲正确,乙错误B.乙正确,甲错误C.甲、乙均正确D.甲、乙均错误
14.如图,一次函数的图象与反比例函数是的图象交于,两点,过点作轴于点,过点作轴于点,连接,.下列结论正确的是()
A.点和点关于原点对称
B.当时,
C.反比例函数中都随的增大而减小
D.的面积等于的面积
15.已知:如图与关于点位似,且位似比为1:3,设的横坐标为,则的对应点的横坐标为()
A.B.C.D.
16.已知二次函数的部分图象如图所示,点是坐标系的原点,点是图象对称轴上的点,图象与轴交于点,则下面结论:
①关于的方程的解是,;②;③若时,,则点的坐标是;④若时,,则周长的最小值是.
其中正确的是()
A.①②B.③④C.①②③④D.①②③
卷Ⅱ(非选择题共78分)
二、填空题(本大题共3个小题,每小题3分,共9分)
17.若,则_______________.
18.如图,在矩形中,平分,,那么的度数为_______________.
19.在平面直角坐标系中,抛物线与轴正半轴有交点,则的取值范围___________,当时,抛物线在轴上方;当时,抛物线在轴下方,则_________.
三、解答题(本大题共7个小题,共69分)
20.(本小题满分7分)关于的一元二次方程.
(1)当时,求的值;
(2)请判断方程根的情况,并说明理由;
(3)若的一个根是,求方程的另外一个根.
21.(本小题满分8分)“这么近,那么美,周末到河北.”越来越多的外地游客利用假期来领略河北优美的自然风光和厚重的历史文化.保定市莲池区某中学组建了一支学生讲解员队伍,到下面四个景区志愿服务.
景区有:直隶总督署—用A表示;古莲花池—用B表示;
淮军公所—用C表示;保定军校博物馆—用D表示,
将编号A,B,C,D分别写在四张卡片上,每名同学随机抽取一张后放回,并到其抽到的景区志愿服务.
(1)小明抽到“直隶总督署”志愿服务的概率是_______________.
(2)小明和小亮是同班同学,求他们抽到同一景区志愿服务的概率.(请用树状图或列表的方法写出分析过程.)
22.(本小题满分8分)小明同学用木板制作一个带有卡槽的三角形支架,如图所示.已知,,,小明的平板宽度为17cm,卡槽与等长,小明同学能否将平板放入卡槽内?请说明你的理由.(提示:,,)
23.(本小题满分9分)如图,在中,,,将绕点逆时针旋转一定的角度()得到,连接、交于点,当时,判断四边形的形状,并说明理由.
24.(本小题满分11分)如图点在函数(是常数,,)的图象上,将点先向下平移4个单位,再向右平移2个单位,得点,点恰好落在函数的图象上.
(1)求函数的解析式;
(2)连接,,,求的面积;
(3)一次函数(,是常数,)经过,两点,直接写出时,的取值范围.
25.(本小题满分12分)如图,在某中学的一场篮球赛中,小明在距离篮圈中心5m(水平距离)远处跳起投篮,已知球出手时离地面2.2m,当篮球运行的水平距离为3m时达到离地面的最大高度4m,设篮球在空中的运行路线为一条抛物线,篮圈中心距地面3m.
(1)建立如图的平面直角坐标系,求篮球运行路线所在抛物线的函数表达式;通过计算说明此球能否投至篮筐中心(不考虑篮球大小和篮球的反弹)
(2)探究一:若出手的角度,力度和高度都不变,则小明朝着篮球架再向前或向后移动多少米投篮能将篮球投至篮中心(结果精确到0.1m,参考数据:)?
探究二:若出手的角度,力度和高度都发生改变的情况下,但抛物线的顶点不变,求小明出手的高度应为多少米才能将篮球投至篮筐中心?
26.(本小题满分14分)如图,在矩形中,,.为中点,直角的直角顶点在边运动,始终过点.设.
(1)求证:;
(2)若与所在的直线有交点,该交点用表示,用含的代数式表是的长,并求出的最大值;
(3)求出当过点时的值.
(4)__________时,为等腰三角形.
2023—2024学年第一学期期末质量监测
九年级数学参考答案
一、选择题
1.D 2.B 3.C 4.C 5.B 6.C 7.D 8.C 9.C 10.D
11.B 12.B 13.C 14.D 15.D 16.D
二、填空题
17.18.19.12
三、解答题
20.(1)当时,,∴,;
(2),∴方程有两个不相等的实数根;
(3)当,,∴.
21.(1)
(2)
共有16种等可能的结果,小明和小亮抽到同一景区志愿服务的结果有4种,(抽到同一景区志愿服务).
22.小明同学能将手机放入卡槽内.
理由:作于点,
∵,,
∴,,
∵,∴,
∴,∵,
∴小明同学能将手机放入卡槽内.
23.旋转角为120°时,四边形是菱形.
∵,,∴.
∵,∴.
∴,∴.
同理,∴四边形是平行四边形,
又∵,∴四边形是菱形.
24.(1)由题意可知,在上,
∴,∴,∴
(2)过点作轴于点,过点作轴于点,
,交于点,则,
∴,∴;
(3).
25.(1)∵抛物线的顶点为,∴设,
把代入,得,∴,
当时,,,∴不能投进.
(2)探究一:当时,,
解得(舍),,.
∴小明向后退0.2m.
探究二:设,把代入,得.
∴,当时,,
∴小明出手的高度应为1.75m.
26.(1)∵,∴,
∵,∴,∴.
(2)∵,,∴,
∴,即,∴,
∴的最大值为.
(3)∵过点,∴,即,解得,.
(4)4,6或.
小亮
小明
相关试卷
这是一份河北省保定市莲池区2023-2024学年上学期八年级上学期期末数学试题,文件包含河北省保定市莲池区2023-2024学年上学期八年级上学期期末数学试题pdf、答案数学pdf等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。
这是一份河北省保定市莲池区2023-2024学年九年级上学期1月期末 数学试题,共9页。
这是一份河北省保定市莲池区2023-2024学年七年级下学期期末数学试题,共11页。








