黑龙江省双鸭山市集贤县2022-2023学年八年级下学期期末数学试题（含答案）

这是一份黑龙江省双鸭山市集贤县2022-2023学年八年级下学期期末数学试题（含答案），共10页。试卷主要包含了单选题，四象限，则k的值是，解答题等内容，欢迎下载使用。
一、单选题（每小题3分，满分30分）
1．下列根式中，化简后能与进行合并的是（ ）
A．B．C．D．
2．若，化简的结果是（ ）
A． B． C． D．
3．如图是楼梯的一部分，若，，，一只蚂蚁在A处发现C处有一块糖，则这只蚂蚁吃到糖所走的最短路程为（ ）
A．B．3C．D．
4．两艘轮船从同一港口同时出发，甲船时速40海里，乙船时速30海里，两个小时后，两船相距100海里，已知甲船的航向为北偏东，则乙船的航向为（ ）
A．南偏东44°B．北偏西44° C．南偏东44°或北偏西44° D．无法确定
5．如图，、两点被池塘隔开，在点A、B外选一点，连接，，并分别找出它们的中点、，连接，现测得＝，则长为（ ）
A．B．C．D．
6．如图，在矩形中，，对角线相于点，，则的长为（ ）
A．8B．4C．D．2
7．如图，在平行四边形中，于于，平行四边形的周长为（ ）
A． B． C．20 D．12
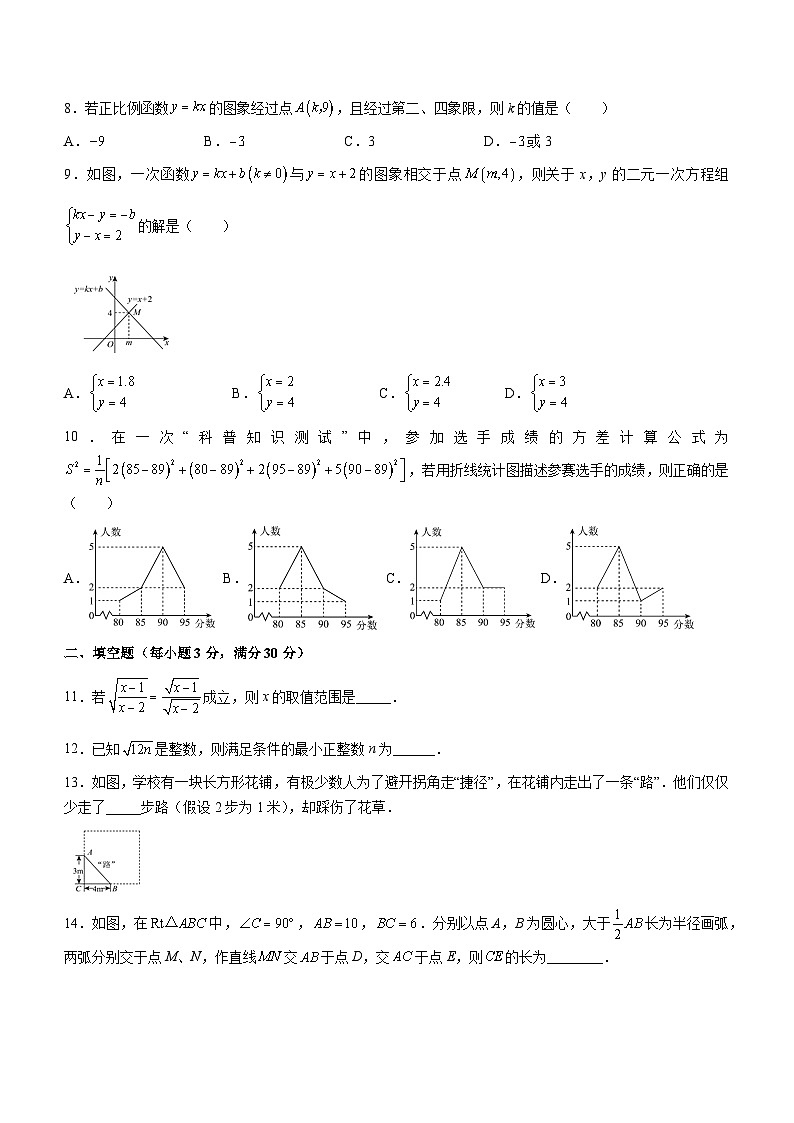
8．若正比例函数的图象经过点，且经过第二、四象限，则k的值是（ ）
A．B．C．3D．或3
9．如图，一次函数与的图象相交于点，则关于x，y的二元一次方程组的解是（ ）
A． B． C． D．
10．在一次“科普知识测试”中，参加选手成绩的方差计算公式为，若用折线统计图描述参赛选手的成绩，则正确的是（ ）
A． B． C． D．
二、填空题（每小题3分，满分30分）
11．若成立，则x的取值范围是_____．
12．已知是整数，则满足条件的最小正整数n为______．
13．如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了_____步路（假设2步为1米），却踩伤了花草．
14．如图，在中，，，．分别以点A，B为圆心，大于长为半径画弧，两弧分别交于点M、N，作直线交于点D，交于点E，则的长为________．
15．如图，在中，，若是AB边的中线，则_____．
16．已知以A、B、C、D四个点为顶点的平行四边形中，顶点A、B、C的坐标分别为，则顶点D的坐标为___________．
17．如图，菱形中，，于点，交于点，于点．若△BFG的周长为6，则菱形的边长为_______．
18．为了了解400名八年级男生的身体发育情况，随机抽取了100名八年级男生进行身高测量，得到统计表，则频数最大一组的组中值为______________．
19．如图，将直线向下平移3个单位得到一个一次函数的图像，那么这个一次函数的表达式为____________．
第18题表格
第20题图
第19题图
A
20.如图，过原点的两条直线分别为，过点作轴的垂线与交于点，过点作轴的垂线与交于点，过点，作轴的垂线与交于点，过点作轴的垂线与交于点，过点作轴的垂线与交于点，依次进行下去，则点的坐标________．
三、解答题（满分60分）
21．计算：（每小题3分，满分6分）
（1） （2）
22.（满分5分）
如图，小丽荡秋千，秋千架高2.4米，秋千座位离地0.4米，小红荡起最高时，坐位离地0.8米．此时小红荡出的水平距离是多少？（ 即小红荡到秋千架两边的最高点B、E两点之间的距离）

秋千侧面图
23.（满分7分）
某中学举办党史知识竞赛，设定满分分，学生得分均为整数，在初赛中，甲、乙两组每组人学生成绩单位：分如下．
甲组：54 62 65 65 67 69 75 87 96 100
乙组：53 61 64 66 73 75 75 78 95 100
（1）以上成绩统计分析表中 ______ ， ______ ．
（2）小明同学说：“这次竞赛我得了分，在我们小组中属中游略偏上”观察上面表格判断，小明可能是______ 组的学生．
（3）若要从甲、乙两组学生中选择一个组参加决赛，你认为应选哪个组？请说明理由．
24.（满分6分）
如图，在四边形中，，过点D作的角平分线交于点E，连接交于点O，．
（1）求证：四边形是菱形；
（2）若，△ACD的周长为36，求菱形的面积．
25.（满分8分）
Ⅰ号无人机从海拔处出发，以的速度匀速上升，Ⅱ号无人机从海拔处同时出发，以的速度匀速上升，经过两架无人机位于同一海拔高度，无人机海拔高度与时间的关系如图．两架无人机都上升了．
（1）b的值为______；
（2）Ⅱ号无人机海拔高度与时间的关系式；
（3）直接写出无人机上升多少分钟时，两架无人机高度差10m．
26．（满分8分）
【问题情境】
（1）如图1，已知是正方形，是对角线上一点，求证：；请你完成证明．
图3

【深入探究】
（2）如图2，在正方形中，点是对角线上一点，，，垂足分别为．，连接，猜想与的数量关系，并证明你的猜想．
【拓展应用】
（3）如图3，在正方形中，若，是上一点，过点作于，于．则最小值为________．
27．（满分10分）
某网店直接从工厂购进A、B两款自拍杆，进货价和销售价如表：
（1）网店第一次用850元购进A、B两款自拍杆共30个，求这两款自拍杆分别购进多少个？
（2）第一次购进的自拍杆售完后，该网店计划再次购进A、B两款自拍杆共80个（进货价和销售价都不变），且进货总价不高于2200元．如何购进A、B两款自拍杆，才能使所获得的销售利润最大？最大利润值为多少？
（满分10分）
如图，在平面直角坐标系中，平行四边形的边在x轴上，已知点，点，连接，直线交y轴于点E，且．
（1）求点C的坐标.
（2）动点P从点A出发，沿折线方向以个单位秒的速度向终点C做匀速运动，若的面积为，点P的运动时间为t秒．
当时，求S与t之间的函数关系式；
在点P运动过程中，当时，直接写出t的值.
2022—2023学年度第二学期期末测试八年级数学参考答案
一、单选题（每小题3分，满分30分）
1．D 2．C 3．D 4．C 5．D
6．B 7．C 8．B 9．B 10．A
二、填空题（每小题3分，满分30分）
11．x>2 12. 3 13. 4 14. 74 15. 1 16．（3,1） 或（-1,1）或（5,3） 17. 6 18. 160 19. y=2x-3 20. （-21011，-21012）
三、解答题（满分60分）
21．（6分，每小题3分）
（1）解：（1）解：；---------------3分
（2）解：．---------------3分
22．（满分5分）解：如图，座位最低点为A，最高点为B，
则OB=OA=OP-AP=2.4-0.4=2（m），…………1分
过B点作的垂线，垂足为点C，
则OC=OP-BN=2.4-0.8=1.6（m）， …………1分
由勾股定理得：
BC=OB2−OC2=22−1.62=1.2（m），…………1分
∴BE=2BC=2×1.2=2.4（m）， …………1分
故小红荡出的水平距离是.…………1分
23.（满分7分）（1（1）；．---------------2分
（2）甲---------------2分
（3）选乙组参加决赛．理由如下：---------------1分
甲、乙两组学生平均数相同，乙组的中位数比甲组的中位数高，，
乙组的成绩比甲组稳定，故选乙组参加决赛．---------------2分
24．（满分6分）（1）证明：∵，，
∴四边形是平行四边形，---------------1分
，
∵平分，
∴，
∴，
∴，---------------1分
∴平行四边形是菱形；---------------1分
（2）解：∵四边形是菱形，
∴，，，，
∵，的周长为36，
∴，---------------1分
则，
在中，，
∴，---------------1分
∴菱形的面积为．---------------1分
25.（满分8分）（1）解：b=60，---------------2分
（2）解：设Ⅱ号无人机海拔高度与时间的关系式为y=kx+b，
将、代入上式得b=3060=5k+b ---------------2分
解得k=6b=30 ---------------1分
∴函数表达式为；，---------------1分
（3）无人机上升2.5分钟或7.5分钟时，两架无人机高度相差10米．---------------2分
26.（满分8分）
（1）解：（1）∵四边形是正方形，
∴，，----------1分
∵，
∴， ----------1分
∴；----------1分
（2）∵PE⊥AB，PF⊥BC，四边形是正方形，
∴∠PEB=∠ABC=∠PFB=90°，
∴四边形PEBF是矩形，----------1分
∴PB=EF ----------1分
又由（1）得PD=PB ∴ ----------1分
（3）．----------2分
27．（满分10分）解：设网店第一次购进x个A款自拍杆，y个B款自拍杆，
根据题意得：--------------1分，
解得：．--------------1分
答：网店第一次购进20个A款自拍杆，10个B款自拍杆；--------------1分
（2）解：设购进m个A款自拍杆，则购进个B款自拍杆，
根据题意得：30m+25（80-m）≤--------------1分
解得：，--------------1分
设再次购进A、B两款自拍杆的销售利润为w元，
则，--------------1分
即．--------------1分
∵，
∴w随m的增大而增大，--------------1分
∴当时，w取得最大值，80-40=40，W最大值．--------------1分
答：A、B两款自拍杆各购进40个时，销售利润最大，最大利润为1080元．-----------1分
28．（满分10分）（1）解：，，点，
，，--------------1分
，--------------1分
，
∵四边形是平行四边形，边在轴上，
轴，， --------------1分
，--------------1分
（2）①如图1，设直线的解析式为，
∵直线经过点，，
，解得，
∴直线的解析式为，--------------1分
，，--------------1分
，，
，--------------1分
，
；--------------1分
②t的值为或．---------------2分
身高（cm）
人数
22
45
28
5
组别
平均数
中位数
众数
方差
甲组
乙组
类别
A款自拍杆
B款自拍杆
进货价（元/个）
30
25
销售价（元/个）
45
37