河北省保定市高碑店市2024-2025学年九年级上学期10月月考数学试题

这是一份河北省保定市高碑店市2024-2025学年九年级上学期10月月考数学试题，共10页。试卷主要包含了请将各题答案填写在答题卡上，下列数中，能使成立的x的值为等内容，欢迎下载使用。
注意事项：
1．满分120分，答题时间为120分钟．
2．请将各题答案填写在答题卡上．
3．本次考试设卷面分，答题时，要书写认真、工整、规范、美观．
一、选择题（本大题共16个小题，共38分．1—6小题各3分．7—16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．下列方程是一元二次方程的是（ ）
A． B． C． D．
2．将一元二次方程化成一般形式后，二次项系数和一次项系数分别为（ ）
A．3， B．3，4 C．3， D．
3．如图，下列直线是该菱形的对称轴的是（ ）

A． B．和 C．和 D．全部都是
4．下列数中，能使成立的x的值为（ ）
A．1 B．2 C．3 D．4
5．如图，点O为正方形的中心，将正方形绕点O顺时针旋转，要使其旋转后能与自身重合，至少需要旋转（ ）
A． B． C． D．
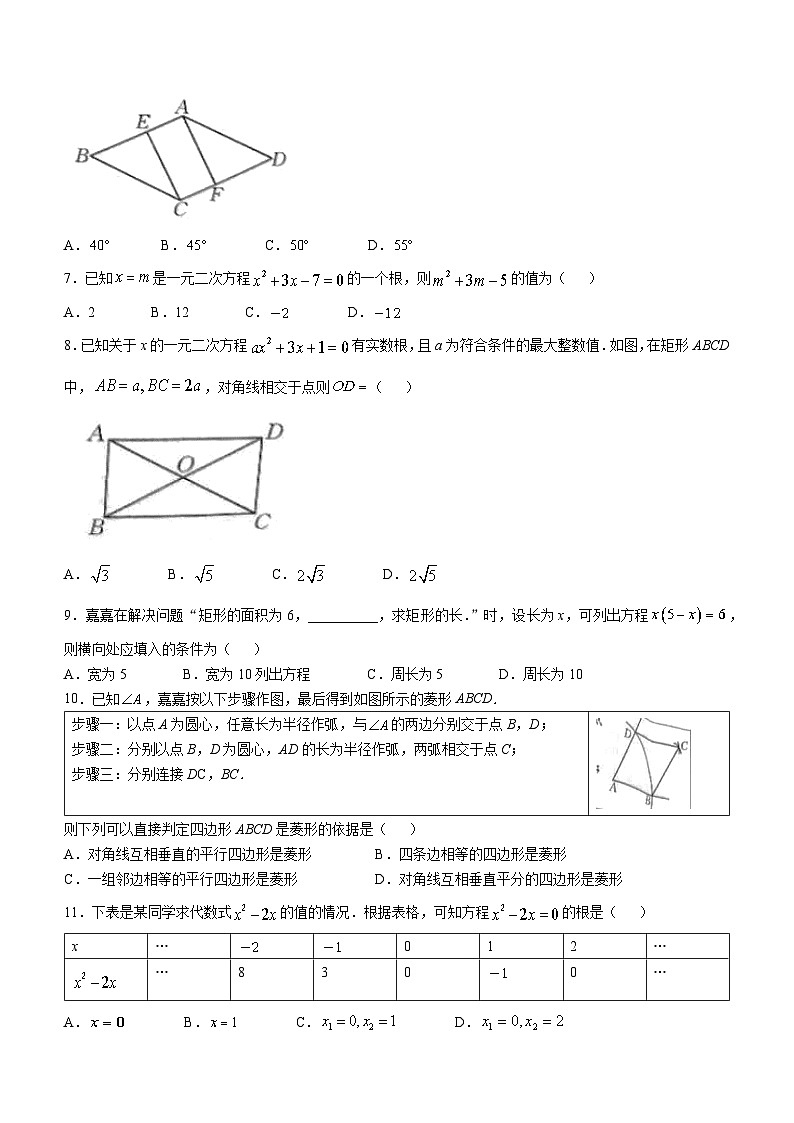
6．如图，在菱形ABCD中，，E，F分别为边AB和CD上的两个动点．当四边形AECF为矩形时，的度数为（ ）
A． B． C． D．
7．已知是一元二次方程的一个根，则的值为（ ）
A．2 B．12 C． D．
8．已知关于x的一元二次方程有实数根，且a为符合条件的最大整数值．如图，在矩形ABCD中，，对角线相交于点则（ ）
A． B． C． D．
9．嘉嘉在解决问题“矩形的面积为6，__________，求矩形的长．”时，设长为x，可列出方程，则横向处应填入的条件为（ ）
A．宽为5 B．宽为10列出方程 C．周长为5 D．周长为10
10．已知，嘉嘉按以下步骤作图，最后得到如图所示的菱形ABCD．
则下列可以直接判定四边形ABCD是菱形的依据是（ ）
A．对角线互相垂直的平行四边形是菱形 B．四条边相等的四边形是菱形
C．一组邻边相等的平行四边形是菱形 D．对角线互相垂直平分的四边形是菱形
11．下表是某同学求代数式的值的情况．根据表格，可知方程的根是（ ）
A． B． C． D．
12．如图，矩形铁板的长为a，在左侧截掉一个最大的正方形．若剩余部分的周长为b，则a与b的关系为（ ）
A． B． C． D．
13．在平面直角坐标系中，我们把一个点的纵坐标与横坐标的乘积称为该点的“点积值”．如图，线段AB位于第一象限，轴，点A在直线上，当点B的“点积值”为28时，点A的横坐标为（ ）
A．3 B．4 C．5 D．6
14．如图，将长为的矩形纸条对折后沿折痕剪开，将剪开后的纸条交叉叠放在一起，测量得知中间重叠四边形的两条对角线的长分别为和，则原矩形纸条的面积为（ ）
A． B． C． D．
15．《九章算术》是我国传统数学中重要的著作之一，奠定了我国传统数学的基本框架．《九章算术》中记载：“今有户高多于广六尺八寸，两隅相去适一丈，问户高、广各几何?”大意；有一形状是矩形的门，它的高比宽多6尺8寸，它的对角线长1丈，问它的高与宽各是多少?利用方程的思想，设矩形门的宽为x尺，则依题意，可列方程（1丈尺，1尺寸）（ ）
A． B．
C． D．
16．如图，在等腰直角三角形ABC中，，D为BC延长线上的一点，且，过点C作，F为CE上的一动点，作矩形ACFG，矩形ACFG的对角线相交于点O，连接DO，则DO的最小值为（ ）
A．4 B．8 C． D．
二、填空题（本大题共3个小题，共10分．17小题2分，18—19小题各4分，每空2分）
17．为加强美丽乡村建设，某地文化馆向某乡村图书馆捐赠图书3次，且每次捐赠图书数量的增长率相同．第1次捐赠图书10000册，第3次捐赠图书12100册．若设捐赠图书数量的增长率为x，则依题意，可列方程： ____________．
18．在用公式法求解一元二次方程时，其中一步的过程为．
根据以上信息，解答下列问题．
（1）a的值为____________．
（2）方程的两根之和为_____．
19．如图，在菱形ABCD中，，正方形EFGH的顶点E，F在边AB和BC上，且．
（1）的度数为______________．
（2）若，则阴影部分的面积为_____________．
三、解答题（本大题共7个小题，共72分．解答应写出文字说明，证明过程或演算步骤）
20．（本题9分）解下列方程．
（1）．
（2）．
21．（本题9分）如图，在四边形ABCD中，，过点D分别作于点E，于点F．
（1）求证：四边形ABCD是菱形．
（2）猜想AE与CF的数量关系，并说明理由．
22．（本题9分）若一个一元二次方程有一个实数根为1，则称为“归一方程”例如：就是“归一方程”．
（1）判断一元二次方程：_______“归一方程”．（填“是”或“不是”）
（2）若关于x的一元二次方程为“归一方程”，且方程有两个相等的实数根，求a和c的值．
23．（本题10分）情境：向阳中学实践小组成员利用矩形的判定方法，验证学校广场中心的花坛MNPQ是否为矩形．
操作：如图，实践小组成员测得米，米．
（1）以上数据可说明花坛为_________．
探究：小组成员甲认为只要再测出MP与NQ的长，即可知道四边形MNPQ的形状是否为矩形，由此他测出米．
（2）请根据成员甲的数据说明四边形MNPQ的形状，并说明理由．（可直接利用（1）中的结论）
（3）小组成员乙认为甲只需测得米，即可判断四边形MNPQ的形状是否为矩形，你同意乙的说法吗?请说明理由．（可直接利用（1）中的结论）
24．（本题10分）这么近那么美，周末到河北．我省各市依托独有的地貌特征发展当地旅游业，同时也促进了旅游地周边的发展．某特产销售店购进一批景点贝壳画，进价为10元/个，市场部门规定售价不能超过进价的3倍，店长整理了几天的销售情况，发现该贝壳画每天的销售量y（个）与销售单价x（元/个）之间满足一次函数关系，部分对应数据如下．
（1）y与x之间的函数关系为______．（不写自变量的取值范围）
（2）若销售该贝壳画每天的利润要达到5000元，求该贝壳画的销售单价．
25．（本题12分）白老师在黑板上出了三道解关于x的一元二次方程的题目．请根据四位同学的求解情况，解答下列问题．
（1）甲同学在求解“题目一：”时，正确求出两个根分别为．请根据甲同学的计算结果，求出b和c的值．
（2）乙同学和丙同学在解“题目二：”时，乙把一次项系数看错了，而解得方程的两根分别为；丙把常数项看错了，解得两根为．请根据乙、丙两位同学的计算结果，求出d和e的值．
（3）丁同学在解“题目三：”时，将a与n的位置互换，他正确地解出了互换后的方程，得到一个根是，而另一个根等于原方程的一个根．请直接写出原方程两根的平方和．
26．（本题13分）如图．在边长为3的正方形ABCD中，E是线段CD上的一个动点，连接AE，以AE为边作正方形AEGF（点F在边AD所在直线的上方），连接DF．
（1）如图1，当点E与点D重合时，直接写出此时DF的长；
（2）如图2，当点E与点C重合时，嘉嘉说：“此时”．淇淇说：“此时正方形AEGF的面积与正方形ABCD的面积的比为2：1．”请选择其中一人的说法进行证明．
（3）如图3，当E为CD的中点时，解答下列问题：
①判断线段AF与DF的数量关系，并说明理由；
②直接写出此时的面积．
2024—2025学年度第一学期第一次月考教学质量监测
九年级数学参考答案
16．C 提示：如图，连接BO．∵四边形ACFG为矩形，∴．
∵，∴BO为AC的垂直平分线．∵，
∴,
当时，OD最短，∴，
∴，∴．
在中，，∴．
17． 18．（1）2 （2）
19．（1） （2）
20．解：（1），
，
， 2分
∴． 4分
（2），
，
∴， 5分
∴ 7分
∴． 9分
21．解：（1）证明：∵，
∴四边形ABCD为平行四边形． 2分
∵，∴四边形ABCD为菱形． 4分
（2）． 5分
理由：∵四边形ABCD为菱形，
∴． 7分
∵，∴，
∴，∴． 9分
22．解：（1）是． 3分
（2）∵为“归一方程”，
∴，∴． 5分
∵方程有两个相等的实数根，
∴， 7分
整理，得，解得， 8分
∴． 9分
23．解：（1）平行四边形． 2分
（2）四边形MNPQ为矩形． 3分
理由：∵四边形MNPQ为平行四边形，，
∴四边形MNPQ为矩形． 5分
（3）同意． 6分
理由：∵米，米，米，
∴，∴． 8分
∵四边形MNPQ为平行四边形，∴四边形MNPQ为矩形． 10分
24．解：（1）． 3分
（2）由题意，得， 6分
解得． 9分
∵，∴ （舍去），∴．
答：该贝壳画的销售单价为20元． 10分
25．解：（1）∵两个根分别为，
∴， 2分
∴． 4分
（2）∵乙把一次项系数看错了，而解得方程的两个根分别为，
∴，即． 6分
∵丙把常数项看错了，解得两根为，
∴，即． 8分
（3）． 12分
提示：令，解得或，故两个方程相同的根为或．
设原来的方程的一个根为，另一个根为，
则．
分两种情况：
①当两个相同的根为1时，则，
∴，∴，
②当两个相同的根为时，则，
∴，∴
综上所述．原方程两根的平方和是
26．解：（1）． 2分
（2）选嘉嘉的说法．
证明：∵四边形ABCD和四边形AEGF均为正方形，
∴， 4分
∴，∴， 5分
∴，∴． 6分
选淇淇的说法．
证明：∵四边形ABCD为正方形，
∴， 4分
∴，∴． 5分
∵，∴． 6分
（3）①．
理由：如图，过点F作于点H，
∴，∴． 7分
∵四边形ABCD和四边形AEGF均为正方形，
∴，
∴，∴． 8分
∵，
∴，∴． 9分
∵E是CD的中点，∴，
∴，∴． 10分
∵，∴FH垂直平分AD，∴． 11分
②的面积为． 12分
步骤一：以点A为圆心，任意长为半径作弧，与的两边分别交于点B，D；
步骤二：分别以点B，D为圆心，AD的长为半径作弧，两弧相交于点C；
步骤三：分别连接DC，BC．
x
…
0
1
2
…
…
8
3
0
0
…
x/（元/个）
…
15
25
…
y/个
…
600
400
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
B
C
C
A
B
A
A
B
D
B
D
A
B
D
C