人教B版 (2019)选择性必修 第一册2.1 坐标法教学ppt课件

这是一份人教B版 (2019)选择性必修 第一册2.1 坐标法教学ppt课件，共21页。PPT课件主要包含了课程标准，坐标法，当堂检测等内容，欢迎下载使用。
解析几何学是借助坐标系，用代数方法研究几何对象之间的 关系和性质的一门几何学分支，亦叫坐标几何.由法国数学家 笛卡尔和费马等人创建.解析几何的核心思想——数形结合几何问题——代数化——处理代数问题——分析 代数结果的几何意义——解决几何问题
教材分析平面解析几何简介
1.掌握数轴上向量的坐标公式，会用向量法推导 出数轴上两点之间的距离公式，中点坐标公式； 2.了解并掌握平面直角坐标系内的两点之间的距 离公式，中点坐标公式及其推导过程3.能用坐标法解决几何问题
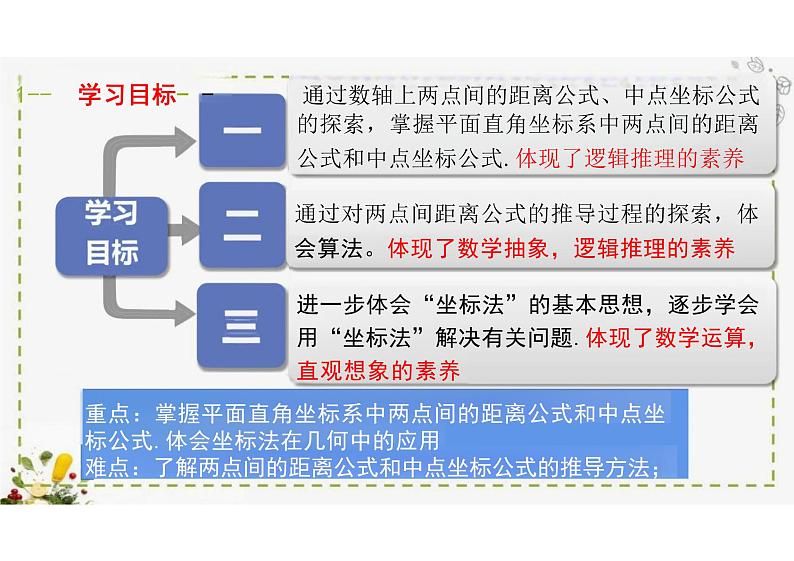
1-- 学习目标- - 通过数轴上两点间的距离公式、中点坐标公式的探索，掌握平面直角坐标系中两点间的距离公式和中点坐标公式.体现了逻辑推理的素养通过对两点间距离公式的推导过程的探索，体 会算法。体现了数学抽象，逻辑推理的素养进一步体会“坐标法”的基本思想，逐步学会 用“坐标法”解决有关问题.体现了数学运算， 直观想象的素养重点：掌握平面直角坐标系中两点间的距离公式和中点坐 标公式.体会坐标法在几何中的应用难点：了解两点间的距离公式和中点坐标公式的推导方法；
给定了原点、单位长度与正方向的直线是数轴，数轴上的点与实数是一一对应的.|AB|=|AB|=|x₂)-(x₁I设AB中 点M(x), 则 答案：12;4已知数轴上A(-2),B(10), 求这两点之间的距离以及它们的中点坐标?
本课导入平面直角坐标系中的基本公式
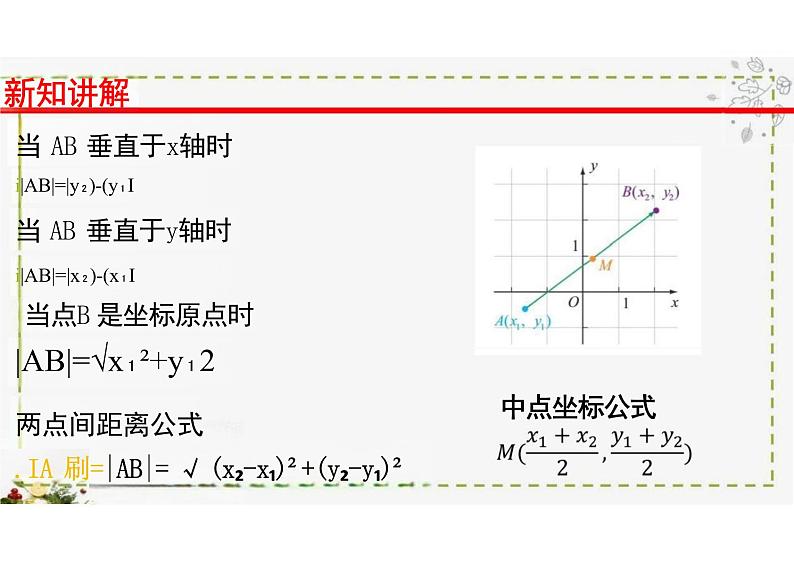
新知讲解当 AB 垂直于x轴时i|AB|=|y₂)-(y₁I当 AB 垂直于y轴时i|AB|=|x₂)-(x₁I当点B 是坐标原点时|AB|=√x₁²+y₁2两点间距离公式.IA 刷=|AB|= √ (x₂-x₁)²+(y₂-y₁)²
两点之间的距离：5;中点坐标 i2.求点A(1,-1) 关于点M(2,3) 的对称点B的坐标。B(3,7)3.已知点A(-3,2) 与 点B(1,0) 关于点M对称，求点M的坐标。
1.已知A(3,0),B(0,-4), 求这两点之间的距离以及它们的中点坐标。
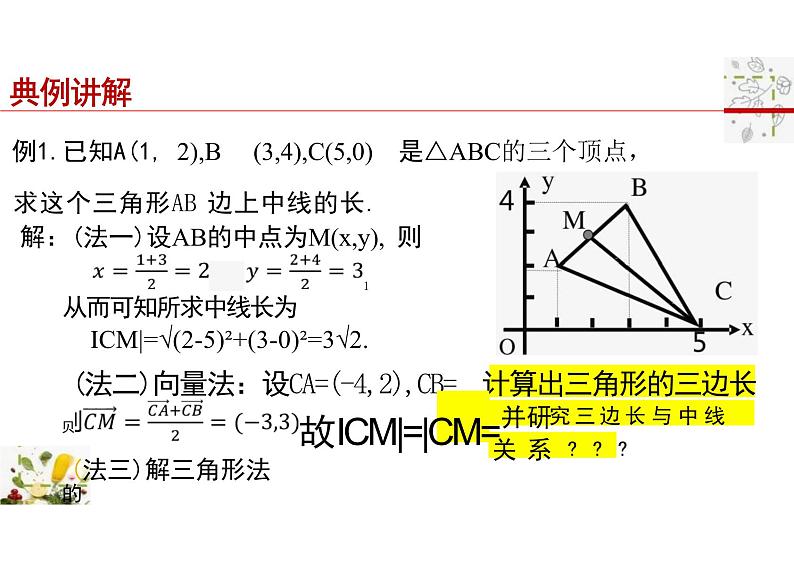
(法二)向量法：设CA=(-4,2),CB= 计算出三角形的三边长(法三)解三角形法
求这个三角形AB 边上中线的长.解：(法一)设AB的中点为M(x,y), 则1从而可知所求中线长为ICM|=√(2-5)²+(3-0)²=3√2.
贝 故ICM|=|CM= 究?三?边?长与中线的
例1.已知A(1, 2),B (3,4),C(5,0) 是△ABC的三个顶点，
尝试与发现D如图2-1-3所示□ABCD 中，如果要证明AC²+BD²=2(AB²+AD²), AB你能想到什么办法? 图2- 1- 3取A为坐标原点，AB 所在直线为x轴 ，建立如图所示的平面直角坐标系.则A(0,0),设 B(a,0),C(b,c), 从而由平行四边形的性质可知D(b-a,c).因此|AC|²=b²+c² |BD|²=(b-2a)²+c²=b²-4ab+4a²+c² |AC|²+|BD|²=2b²-4ab+4a²+2c²;类似地|AB|²=a², |AD|²=(b-a)²+c²=b²-2ab+a²+c²,从而可以看出AC|²+|BD|²=2(|AB|²+|ADI²).
结论：平行四边形两条对角线的平方和等于它的四条边的平方和
思考：能否 借助解三角 形的知识来 解决此问题?
典例讲解 例2:已知ABCD 是一个长方形，AB=4,AD=1, 判断线段CD 上是否存在点P, 使得AP⊥BP. 如果存在，指出满足条件的P有多少介；如果不存在，说明理由.
解：以AB的中点为原点，AB 所 在直线为x轴建立直角坐标系
A(-2,0),B(2,0),C(2,1),D(-2,1).设P(t,1)是线段CD上的一点，则-2≤t≤2 个y而且 PA=(-2-t,-1),PB=(2-t,-1).因为AP ⊥BP的充要条件是PA⊥PB, A O B又因为上述方程的解为t=√3
即PA PB=0, 这也等价于(-2-t)(2-t)+1=0.
所以满足条件的P点存在，而且有
归纳总结坐标法的基本步骤1.建立适当的坐标系，用坐标表示有关的量； 2.进行有关的代数运算；3.将代数结果翻译成几何关系.
跟踪练习 1.已知A(3,1),B(-2,2), 在 y轴上的点P满足PA⊥PB,求P的坐标。参考答案：P(0,4) 或(0,- 1)
课堂小结1.解析几何的基本思想和研究方法2.平面直角坐标系中两点间的距离公式与中点坐标公式 3.坐标法解决问题的一般方法与基本步骤1.坐标法(几何与代数的转化)数学思想方法 2.数形结合3.转化与化归核心素养：数学抽象，逻辑推理，数学运算，直观想象
:: ∴D(1,7).∴|CD|=√(1-1)²+(7-5)²=2.2.已知平行四边形ABCD的两个顶点坐标分别为A(4,2),B( 5,7), 对 角线交点为E(-3-,4), 两顶点C,D 的坐标为(-10,6) (-11.1。)-
B.4 C 口解析 —
1.已知A(3,1),B( 2,4),C(1,5), 且 点A关于点B的对称点为D, 则|CD|=
由题意知B为AD的中点，设D(x,y),
取BC 边所在直线为x轴，边BC 的中点为原点，建立直角坐标系，如图所示。设B(—a,0),C(a,0),A(m,n) (其中a>0),则|AB|²+|ACl²=(m+a)²+n²+(m—a)²+n²=2(m²+a²+n²),|AO|²+|0C|²=m²+n²+a²,∴|AB|²+|ACl²=2(|AO|²+|OCl²).
3.已知AO 是△ABC 中BC 边的中线，证明： |ABl²+|AClP=2(|AO l²+|0Cl²).证明
IA.3 析- B.4√2 0. 5√2 D.7√2f(x)=√ (x+2)²+16+√ (x+1)²+9,可理解为点(x,0) 到A(一2,4)的距离与到B(一1,3)的距离之和的最小值 ，A(一2,4)关于x轴的对称点为A'(一2,—4),连接A'B,则A'BI= √ 1+49=5 √2, 此为f(x)的最小值.
4.著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休.”事实上，有很多代数问题可以转化为几何问题加以解决，如： √(x—a)²+(y-b) ²可以转化为平面上点M(x,y) 与点N(a,b) 的距离，结合上述观点，可得f(x)= Wx²+4x+20+√x²+2x+10 的最小值为
必做：P70习题2-1A第3、4、5题；P70 习题2-1B第3题选做：P70练习C组 1 , 2 题
数无形时少直觉，形少数时难入微， 数与形，本是相倚依，焉能分作两边 飞。---华罗庚