高中数学人教B版 (2019)选择性必修 第一册2.6.2 双曲线的几何性质教学ppt课件

这是一份高中数学人教B版 (2019)选择性必修 第一册2.6.2 双曲线的几何性质教学ppt课件，共27页。PPT课件主要包含了课程标准，学习目标三等内容，欢迎下载使用。
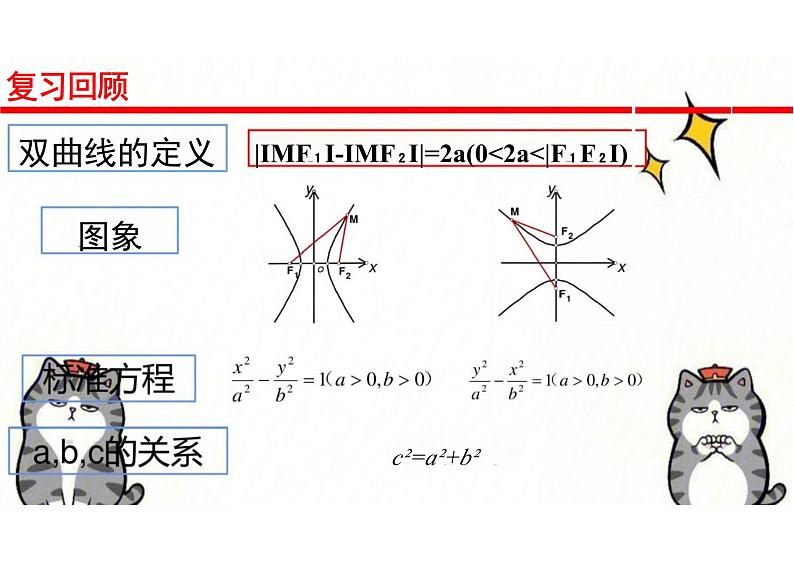
复习回顾双曲线的定义 |IMF₁I-IMF₂I|=2a(0a 时， √x2-a²< √x²=x,这说咀在第一象限内，双曲线一定在直线 的下方；又因 为此时如果x越来越大，则√x²-a²≈ √x²=x,双曲线会越来越接近直
第二象限 第三象限
新知讲解从几何直观上来看：双曲线在四个象限，四个方向上无限接近两条直线y=± 但又始终不相交，从代数角度上来看：计算双曲线上的点P(x,y)到渐近线的距离d,对于第一象限：当x→+0,d→0, 但是d≠0无限接近，但又始终不相交，我们把这两条直线叫做双曲线的渐近线双曲线怎样做，才更准确?
5 . 离心率同椭圆的情形一样，双曲线的半焦距与半长轴长之比
(1)根据双曲线离心率的定义，判断双曲线离心率的取值范围；a>0, 所 以e>1.
所以e越趋近于1,b的值越小，双曲线的渐近线所夹的双曲线区域越狭窄.a
(2)猜想双曲线离心率的大小与双曲线的形状有什么联系，并尝
试证明.x²-y²=1
例1.求下列方程表示的双曲线的实轴长、焦点坐标、离解 ：
(2)双曲线的方程可化双曲线的焦点在y轴上，且a²=b²=9,实轴长2a=6.又因为c²=a²+b²=18, 即c=3 √2.因此，双曲线焦点坐标为(0,-3y2,(0,32).渐近线方程为y=±x.
(1)由标准方程知双曲线焦点在x轴上，且a²=9,b²=16,因此实轴长2a=6.因此，双曲线焦点坐标为(-5,0),(5,0).
以及渐近线方程： (2)x²-y²=+.
又因为c²=a²+b²=25, 即c=5.
解 将 9y²—4x²=—36变形 所以a=3,b=2,c=√ 13,因此顶点坐标为(一3,0),(3,0),
延伸探究：求双曲线9y²-4x²=-36 的顶点坐标、焦点长、虚轴长、离心率和渐近线方程.
实轴长是2a=6, 虚轴长是2b=4,渐近线方程
焦标为(- √ 13,0),(N13,0),
反思感悟由双曲线的标准方程求几何性质的一般步骤化标准- 对于非标准形式的双曲线方程要先化成标准形式定位置 根据方程确定焦点在x 轴上还是在y 轴上求参数- 写出a²,b² 的值，由a²+b²=c² 得出c² 的值根据上面所求a,b,c, 由焦点所在的坐标轴得出所写性质- 求的几何性质
解 依题意可知，双曲线的焦点在y轴上，且c=13, 9∴a=5,b²=c²—a²=144,
一个焦点为(0,13),且离心率为
例2 求适合下列条件的双曲线的标准方程：
确时，应注意分类讨论，也可以不分类讨论直接把双曲线方程设成mx²+ny²=1(mn< 0),从而直接求出来.
由双曲线的几何性质求双曲线的标准方程常用待定系数法，当焦点位置明确时直接设出双曲线的标准方程即可；当焦点位置不明
数学思想方法：“类比学习法”和“数形结合法”核心素养：直观想象，逻辑推理，数学运算
1.等轴双曲线的离心率是\2.( √)2.椭圆的离心率与双曲线的离心率取值范围相同. (×)3.双曲 ,b>0) 的渐近线方程为 (×)4.中心在原点，实轴长为10,虚轴长为6的双曲线的标准方程是(B )
课堂作业必 做：P155练习A 第1、3题；练习B第1,2题
选 做 ：P155练习A组2题，练习B组第5题
天才在于积累，聪明在于勤奋 ---华罗庚
(2)渐近线方程为 ,且经过点A(2,-3); 解 ∵ 双曲线的渐近线方程为(1)若焦点在x 轴上，设所求双曲线的标准方程 ∵A(2,—3) 在双曲线上，由①②联立，无解.(2)若焦点在y 轴上，设所求双曲线标准方程市 @, —3)在双曲线上，一由3④联立，解得a²=8,b²=32.∴所求双曲线的标准方程
b>0), 则b>0), 则