高中数学人教B版 (2019)选择性必修 第一册第二章　平面解析几何2.7 抛物线及其方程2.7.2 抛物线的几何性质教学ppt课件

这是一份高中数学人教B版 (2019)选择性必修 第一册第二章　平面解析几何2.7 抛物线及其方程2.7.2 抛物线的几何性质教学ppt课件，共24页。PPT课件主要包含了O课堂总结等内容，欢迎下载使用。
1.通过研究抛物线的方程，掌握抛物线的几何性质. 2.能利用抛物线的几何性质进行简单应用.
O O课堂总结
O O学习目标
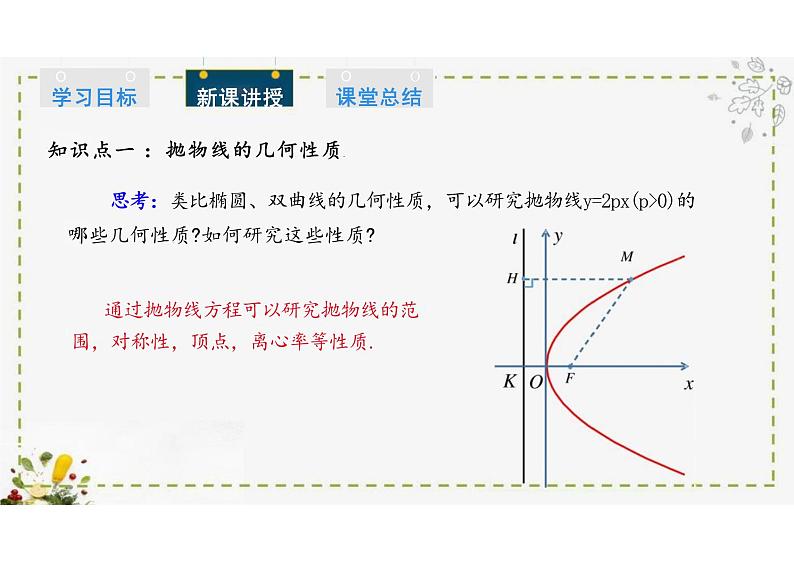
知识点一 ：抛物线的几何性质思考：类比椭圆、双曲线的几何性质，可以研究抛物线y=2px(p>0)的
哪些几何性质?如何研究这些性质?通过抛物线方程可以研究抛物线的范 围，对称性，顶点，离心率等性质.
O O学习目标
O O课堂总结
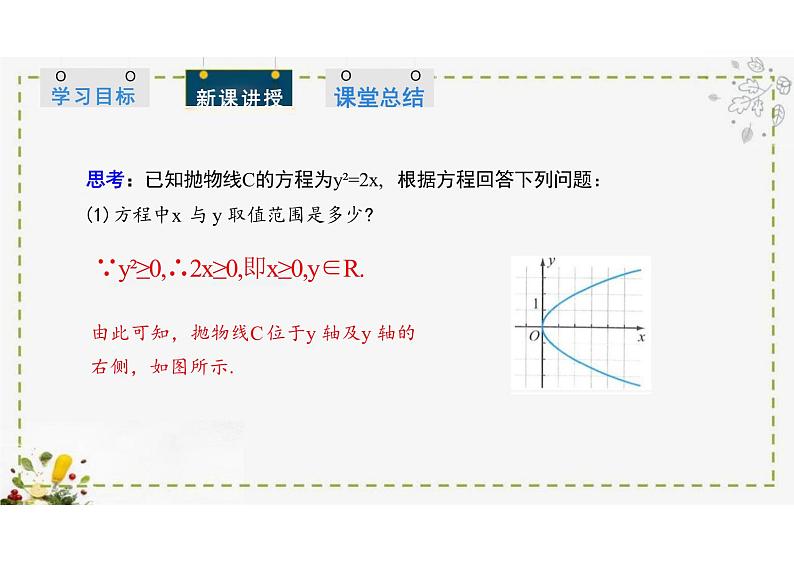
(1)方程中x 与 y 取值范围是多少?∵y²≥0,∴2x≥0,即x≥0,y∈R.由此可知，抛物线C 位于y 轴及y 轴的 右侧，如图所示.
思考：已知抛物线C的方程为y²=2x, 根据方程回答下列问题：
(2)抛物线C 是否关于x轴 ，y 轴，原点对称?为什么?如果(x,y) 是方程y²=2x 的一组解，可得(x,-y) 也是方程的解，即抛物线关于x 轴对称；又因为(-x,y),(-x,-y) 不一定是方程的解， 即抛物线不关于y 轴和原点对称.
思考：已知抛物线C 的方程为y²=2x,根据方程回答下列问题：
O O学习目标
O O课堂总结
(3)抛物线C 与坐标轴是否有交点?如果有，求出交点坐标.令y=0,得 x=0;令x=0,得 y=0.所以抛物线C 与 x 轴 、y 轴都只有一个交点，且交点都是原点(0,0).如图所示.
思考：已知抛物线C 的方程为y²=2x, 根据方程回答下列问题：
O O课堂总结
由方程①可知，2px≥0, 又∵p>0,∴x≥0.∴除顶点外，抛物线上的其余点都在y 轴的右侧.当x→+ 时， |y|→+, 这说明抛物线向右上方 和右下方无限延伸，如图所示 .此时，称抛物线C 的 开口向右(或朝右).
一般地，如果抛物线C 的标准方程是y²=2px(p>0) ① 则可以根据方程①来得到抛物线的几何性质：(1)范围
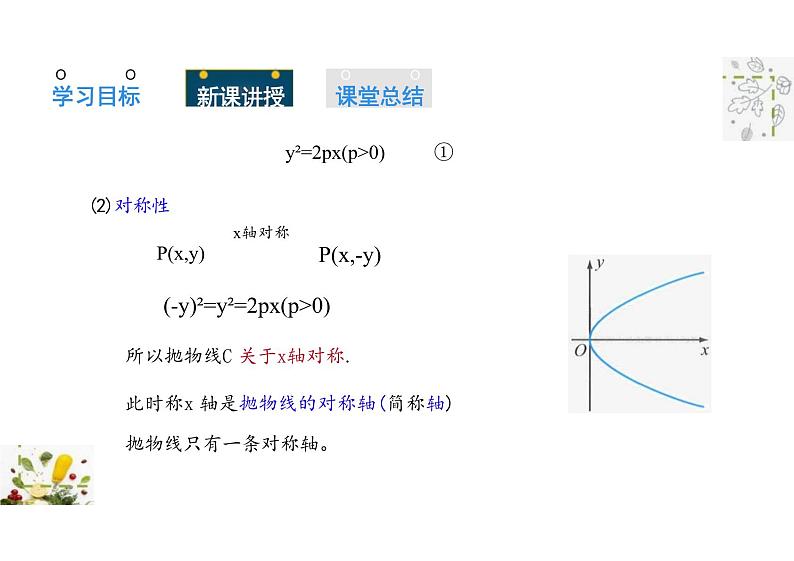
(-y)²=y²=2px(p>0)所以抛物线C 关于x轴对称.此时称x 轴是抛物线的对称轴(简称轴) 抛物线只有一条对称轴。
y²=2px(p>0) ①x轴对称P(x,-y)
(2)对称性P(x,y)
O O学习目标
y²=2px (p>0) ①(3)顶点在方程①中，令y=0,得 x=0;令 x=0,得 y=0. 可知抛物线C 与 x 轴 、y 轴都交于原点(0,0).此时，称原点是抛物线的顶点.
O O学习目标
O O学习目标 新课讲授 课堂总结y²=2px (p>0) ①(2)离心率抛物线上的点到焦点的距离与到准线的距离之 比称为抛物线的离心率，用e 表示.根据抛物线的定义可知，抛物线的离心率
说出抛物线的范围(开口方向)、对称性、顶点、离心率，同①表示的抛物线相比，有什么变化?
y²=-2px(p>0)x²=2py(p>0) x²=-2py(p>0)
思考：如果抛物线的标准方程是
四种抛物线的几何性质的对比
例 1 已知抛物线的对称轴为x 轴，顶点是坐标原点且开口向左，又抛物线经过点M(-4,2√3), 求这个抛物线的标准方程.解：根据已知条件可设抛物线的标准方程为y²=-2px(p>0)∵ 点M(-4,2√3) 在抛物线上，∴(2 √3)²=-2p×(-4) ∴2p=3从而所求方程为y²=-3x
知识点二：抛物线几何性质的简单应用
用待定系数法求抛物线方程的步骤根据条件确定抛物线的焦点在哪条 坐标轴上及开口方向根据焦点和开口方向设出标准方程 根据条件列出关于p的方程解方程，将p代入所设方程为所求
定位置设方程 寻关系 得方程
1.以x轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8,若抛物线的顶点在坐标原点，则其方程为( C )A.y²=8x B.y²=-8xC.y²=8x或y²=-8x D.x²=8y或x²=-8y
O O课堂总结
例2 求抛物线y²=4x上的点P(x,y)到(0,3)的距离与到准线距离之和的最小值.解：如图所示，设此抛物线的焦点为F(1,0), 准线l:x=-1.过点P 作PM⊥l, 垂足为M.则|PM|=|PF|.设Q(0,3), 因此当F,P,Q 三点共线时， |PF|+|PQ| 取得最小值.
.(PF|+IPQD=IQF=√3²+l²=√ 10.即|PM|+|PQ|的最小值为10.
已知P为抛物线 上的动点，P 在x轴上的射影为H, 点A的坐标为(12,6),则 |PA|+|PH|的最小值是( B )A.13 B.12
方法一解：设A(x,y₁),B(x₂,y₂), 直线l方程y=x-1与抛物线的标准方程y²=4x 联立可得x²-6x+1=0.解方程得x=3+2 √2,x₂=3-2 √2,因为 y₂=x₂-1,y =x₁-1,所以y₁=2+2√2,y₂=2-2√2,因此|AB|= √ (x₂-x)²+(y₂-y)²=8.
例3 斜率为l的直线l经过抛物线y²=4x 的焦点F, 且与抛物线相交于A,B 两点，求线段AB的长.
有几种方法求出线段AB的长?
交于A,B 两点，求线段AB的长.方法二解：由题意可知， 焦点F的坐标为(1,0), 准线方程为x=-1.如图，设A(x₁,y),B(x₂,y₂) ,A,B 两点到准线的距离分 别为dA,dg. 由抛物线的定义，可知AF=dA=x₁+1,BF=dp=X₂+1
例3 斜率为l的直线l经过抛物线y²=4x 的焦点F, 且与抛物线相
于是 |AB|=|AF|+|BF|=x+x₂+2,
交于A,B 两点，求线段AB的长.因为直线l的斜率为1,且过焦点F(1,0), 所 以直线l的方程为 y=x-1 ①将①代入方程y²=4x, 得(x-1)²=4x, 化简，得
x²-6x+1=0.所以 x+x₂=6,AB=x+x₂+2=8. 所以，线段AB的长是8.
例4 斜率为1的直线l经过抛物线y²=4x 的焦点F, 且与抛物线相
(1)利用两点间的距离公式的方法最直接，具有一般性，但是计算稍 显复杂；(2)数形结合方法充分运用抛物线的定义：抛物线上的点到焦点的距 离等于这个点到准线的距离，使运算的复杂性大大简化.
O O学习目标
O O课堂总结
归纳总结 过抛物线焦点的直线与抛物线交于两点这两点 间的线段叫做抛物线的焦点弦.
y²=2px(p>0)
当焦点弦垂直于抛物线的对称轴时，称为抛物线的通径.AB=2pp刻画了抛物线开口的大小：
p值越大，开口越宽；p 值越小，开口越窄. y²=2 px(p>0)