高中数学人教B版 (2019)选择性必修 第一册2.6.1 双曲线的标准方程教学课件ppt

这是一份高中数学人教B版 (2019)选择性必修 第一册2.6.1 双曲线的标准方程教学课件ppt，共20页。PPT课件主要包含了O新课讲授，③ac，O课堂总结，①+②÷2得，a0b0等内容，欢迎下载使用。

1.了解双曲线的定义。2.掌握双曲线的标准方程及其图形表示.3.会利用双曲线的定义和标准方程解决问题。
O O课堂总结
情景：如图所示，某中心O接到其正西、正东、正北方向三个观测点A,B,C 的报告：A,C 两个观测点同时听到了一声巨响，B 点听到的时间比A点 晚4s, 已知各观测点到该中心的距离都是1020 m. 假定当时声音传播速度为340m/s, 发出巨响位置为点P, 且A,B,C,O,P 均在同一平面内.该怎样确定巨响发生的点的位置?分析：A,C 同时听到响声，则P在AC 的垂直平分线上；因为观测点B听到声音比A晚4s, 则P 距离B更远，且
|PBI-|PA|=4×340=1360.满足上式的点P的位置组成什么图形呢?
知识点 一 ：双曲线的定义
O O学习目标
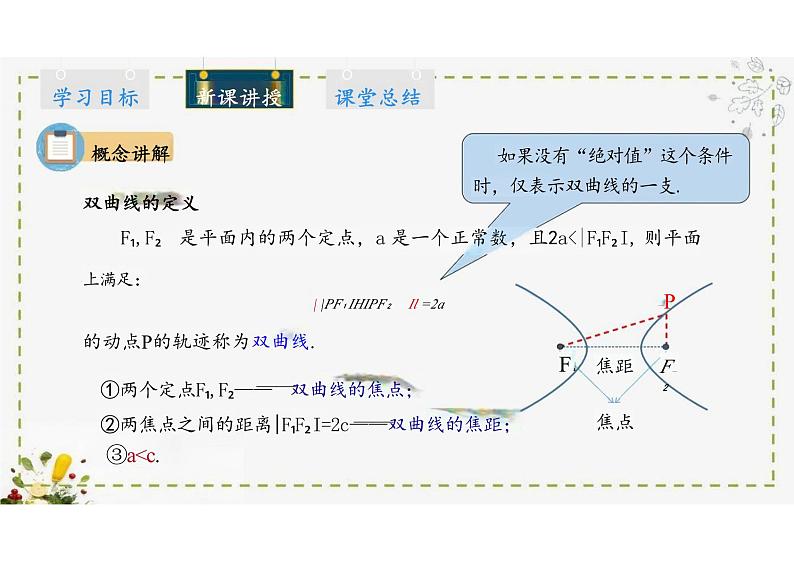
F₁,F₂ 是平面内的两个定点，a 是一个正常数，且2a<|F₁F₂ I, 则平面上满足：| |PF₁IHIPF₂ Il =2a P
的动点P的轨迹称为双曲线.①两个定点F₁,F₂—— 双曲线的焦点；②两焦点之间的距离|F₁F₂ I=2c——双曲线的焦距；
O O O O学习目标 新课讲授 课堂总结
如果没有“绝对值”这个条件时，仅表示双曲线的一支.
如图，将拉链的一边截去一部分，将两端用图钉固定在两定点F₁,F₂ 处 .将笔尖放在拉锁处，随着拉链沿不同部分拉开，笔尖就会画出一条曲线.调换 拉链两端，重复刚才操作，画出另一条曲线.问 题 ：上述操作画出的曲线有什么特点?是什么曲线?曲线上的点到定点F₁,F₂ 的距离之差为定值.曲线为双曲线.
O O课堂总结
以F₁,F₂ 所在直线为x轴，线段F₁F₂ 的垂直平分线为y轴，建立平面直角坐标系.
问题2:类比求椭圆标准方程的过程，如何建立适当的坐标系，得出双曲
知识点2:双曲线的标准方程
O O学习目标
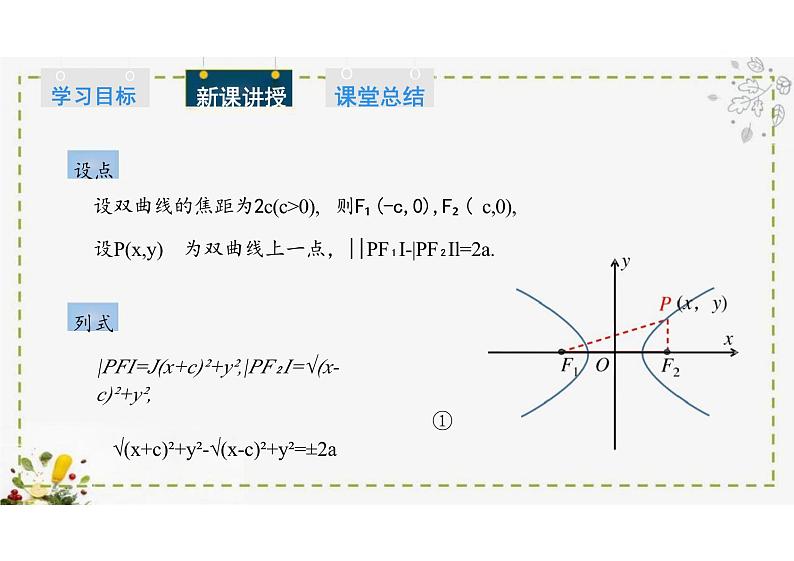
设双曲线的焦距为2c(c>0), 则F₁ (-c,0),F₂ ( c,0),设P(x,y) 为双曲线上一点，||PF₁I-|PF₂Il=2a.
|PFI=J(x+c)²+y²,|PF₂I=√ (x-c)²+y²,√(x+c)²+y²-√(x-c)²+y²=±2a
O O课堂总结
双曲线上任意一点的坐标(x,y) 都是方程③的解；
因为c>a>0, 所以令b²=c²-a²,且b>0, 则可得：
O O学习目标
通常称为焦点在x轴上的双曲线的标准方程.
方程是什么?如图，双曲线的焦距为2c, 焦点分别是 F₁ (0,-c),F₂ (0,c).a,b 的意义同上，这 时双曲线的方程是
思考2:类比焦点在y轴上的椭圆标准方程，焦点在y轴的双曲线的标准
O O学习目标
O O课堂总结
O O课堂总结
思考3: 如何根据双曲线的方程，判断焦点所在的坐标轴?如果x²的系数是正的，则焦点在x轴上；如果y²的系数是正的，则焦点在y轴上.记忆口诀：化成标准形式，焦点跟着正项走
例 1 分别求适合下列条件的双曲线的标准方程：(1)两个焦点的坐标分别是(-5,0),(5,0)且双曲线上的点与两焦点距 离之差的绝对值等于8.(2)双曲线的一个焦点坐标是(0,6),且双曲线过点A(-5,6)解：(1)由已知得c=5,2a=8, 所 以a=4,b²=c²-a²=9.因为焦点在x轴上，所以所求方程为
(2)双曲线的一个焦点坐标是(0,6),且双曲线过点A(-5,6).(2)由已知得另一焦点坐标是(0,6),c=6.因为A 在双曲线上，所以A 到两焦点距离之差的绝对值是
所以a=4,b²=c²-a²=20.又因为焦点在y轴上，因此所求方程是
例2 已知F₁ (-2,0),F₂ (2,0), 动点P满足|PF₁I-IPF₂I=2求动点P 的轨迹方程.解：因为 所以根据双曲线的定义可知，P 一定在a=1,c=2, 且焦点在x轴上的双曲线上，点P的坐标(x,y) 一定满足
归纳总结1.求双曲线标准方程的步骤：(1)确定双曲线的类型，并设出标准方程；(2)求出a²,b²的值，写出标准方程.2.当双曲线的焦点所在坐标轴不确定时，需分焦点在x轴上和y轴上两 种情况讨论，特别地，当已知双曲线经过两个点时，可设双曲线的方 程为Ax²+By²=1(AB<0)来求解.
O O课堂总结
由题可得：P 直线y=-x上，且在以A 、B为焦点的双曲线的左支上.对于双曲线：由条件可得： ,C=1020所以：b²=c²-a²=5×340²其方程为：
问题3:课本P137页情境中，巨响发生的点的位置如何确定?如图，以O为原点，AB 、OC 所在直线为x轴 、y
轴建立平面直角坐标系，
所以，点P在中心O的西北方向的680√10m处.