数学八年级上册第十二章 全等三角形12.2 三角形全等的判定精品学案设计

这是一份数学八年级上册第十二章 全等三角形12.2 三角形全等的判定精品学案设计，文件包含专题122三角形全等的判定基础篇十大题型举一反三人教版原卷版docx、专题122三角形全等的判定基础篇十大题型举一反三人教版解析版docx等2份学案配套教学资源，其中学案共45页， 欢迎下载使用。

TOC \ "1-3" \h \u
\l "_Tc16661" 【题型1 利用SSS证明三角形全等】 PAGEREF _Tc16661 \h 1
\l "_Tc3575" 【题型2 SSS与全等三角形的性质综合应用】 PAGEREF _Tc3575 \h 2
\l "_Tc18828" 【题型3 利用SAS证明三角形全等】 PAGEREF _Tc18828 \h 4
\l "_Tc14863" 【题型4 SAS与全等三角形的性质综合应用】 PAGEREF _Tc14863 \h 5
\l "_Tc8431" 【题型5 利用ASA证明三角形全等】 PAGEREF _Tc8431 \h 6
\l "_Tc7303" 【题型6 ASA与全等三角形的性质综合应用】 PAGEREF _Tc7303 \h 7
\l "_Tc19653" 【题型7 利用AAS证明三角形全等】 PAGEREF _Tc19653 \h 9
\l "_Tc30702" 【题型8 AAS与全等三角形的性质综合应用】 PAGEREF _Tc30702 \h 10
\l "_Tc5114" 【题型9 利用HL证明三角形全等】 PAGEREF _Tc5114 \h 11
\l "_Tc13230" 【题型10 HL与全等三角形的性质综合应用】 PAGEREF _Tc13230 \h 12
知识点1：由边边边（SSS）证明两个三角形全等
三边分别相等的两个三角形全等，简写成“边边边”或“SSS”．
当三角形的三边确定后，其形状、大小也随之确定．这也是三角形具有稳定性的原因．
【题型1 利用SSS证明三角形全等】
【例1】（23-24八年级·山西晋中·期末）如图1是某款雨伞的实物图，图2是该雨伞部分骨架示意图．测得AB=AC，点E，F分别是AB，AC的三等分点，ED=FD，那么△AED≌△AFD的依据是（ ）
A．SASB．ASAC．AASD．SSS
【变式1-1】（23-24八年级·全国·课后作业）如图所示，AD=BC，AC=BD，用三角形全等的判定“SSS”可证明△ACD≌ 或△ABD≌ ．

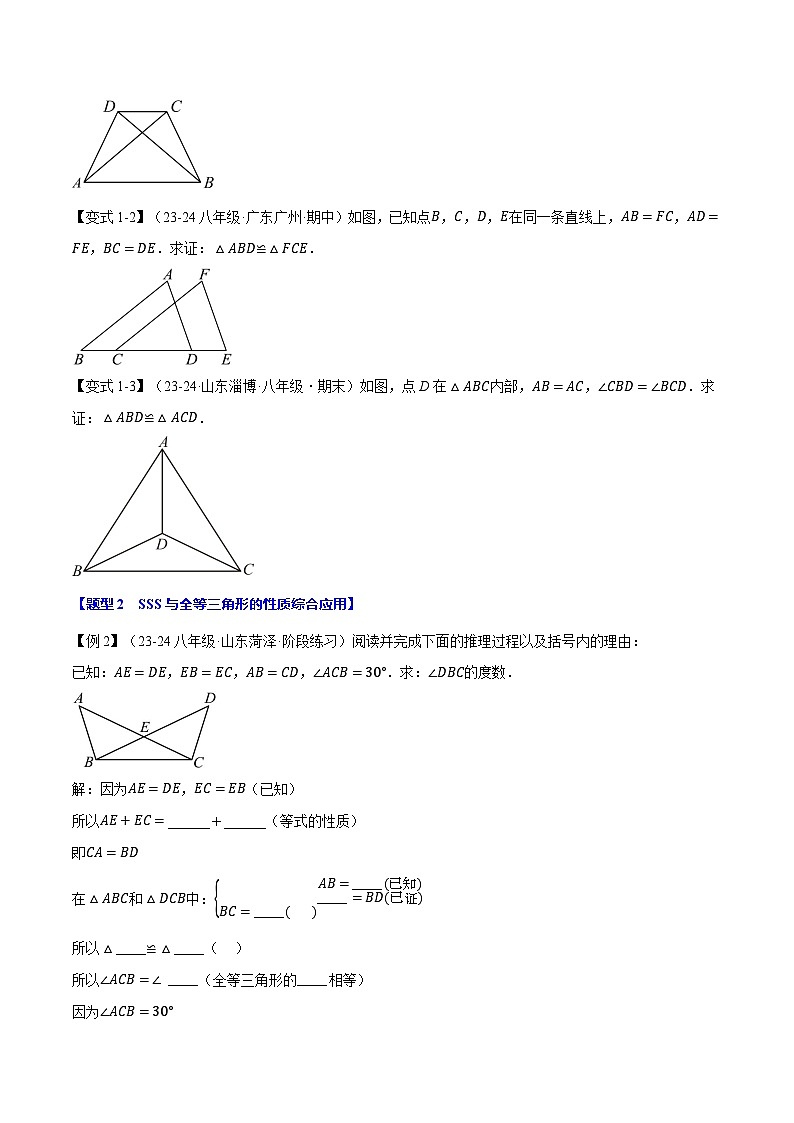
【变式1-2】（23-24八年级·广东广州·期中）如图，已知点B，C，D，E在同一条直线上，AB=FC，AD=FE，BC=DE．求证：△ABD≌△FCE．
【变式1-3】（23-24·山东淄博·八年级·期末）如图，点D在△ABC内部，AB=AC，∠CBD=∠BCD．求证：△ABD≌△ACD．

【题型2 SSS与全等三角形的性质综合应用】
【例2】（23-24八年级·山东菏泽·阶段练习）阅读并完成下面的推理过程以及括号内的理由：
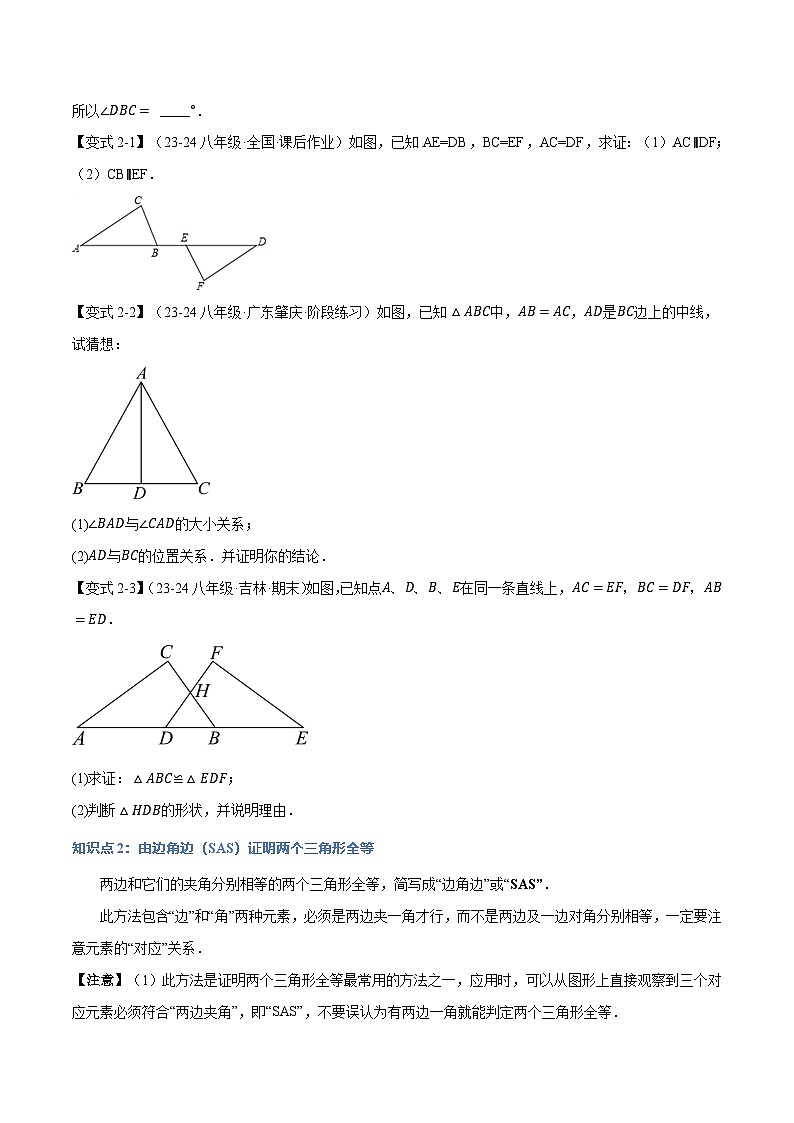
已知：AE=DE，EB=EC，AB=CD，∠ACB=30°．求：∠DBC的度数．
解：因为AE=DE，EC=EB（已知）
所以AE+EC=______＋______（等式的性质）
即CA=BD
在△ABC和△DCB中：&&AB=______已知______=BD已证BC=______
所以△______≌△______（ ）
所以∠ACB=∠ ______（全等三角形的______相等）
因为∠ACB=30°
所以∠DBC= ______°．
【变式2-1】（23-24八年级·全国·课后作业）如图，已知AE=DB，BC=EF，AC=DF，求证：（1）AC∥DF；（2）CB∥EF．
【变式2-2】（23-24八年级·广东肇庆·阶段练习）如图，已知△ABC中，AB=AC，AD是BC边上的中线，试猜想：
(1)∠BAD与∠CAD的大小关系；
(2)AD与BC的位置关系．并证明你的结论．
【变式2-3】（23-24八年级·吉林·期末）如图，已知点A、D、B、E在同一条直线上，AC=EF，BC=DF，AB=ED．

(1)求证：△ABC≌△EDF；
(2)判断△HDB的形状，并说明理由．
知识点2：由边角边（SAS）证明两个三角形全等
两边和它们的夹角分别相等的两个三角形全等，简写成“边角边”或“SAS”．
此方法包含“边”和“角”两种元素，必须是两边夹一角才行，而不是两边及一边对角分别相等，一定要注意元素的“对应”关系．
【注意】（1）此方法是证明两个三角形全等最常用的方法之一，应用时，可以从图形上直接观察到三个对应元素必须符合“两边夹角”，即“SAS”，不要误认为有两边一角就能判定两个三角形全等．
（2）在书写时也要按照“边→角→边”的顺序排列条件，必须牢记“边边角”不能作为判定两个三角形全等的条件．
【题型3 利用SAS证明三角形全等】
【例3】（23-24八年级·河南郑州·期末）如图，小明要测量水池的宽AB，但没有足够长的绳子，聪明的他想了如下办法：先在地上取一个可以直接到达A点和B点的点C，连接AC并延长到D，使CD=CA，连接BC并延长到E，使CE=CB，连接DE并测量出它的长度，则DE的长度就是AB的长，理由是根据 （用简写形式即可），可以得到△ABC≌△DEC，从而由全等三角形的对应边相等得出结论．

【变式3-1】（23-24八年级·江苏宿迁·阶段练习）如图，点E、F在AC上，AD=BC，DF=BE，要用SAS证△ADF≌△CBE，则需添加的条件为 ．
【变式3-2】（23-24·云南昆明·八年级·期末）如图，AD=AE，AC=AB．求证：△ACD≌△ABE．

【变式3-3】（23-24八年级·陕西咸阳·期中）如图，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE，连接BE，求证：△ACD≌△BCE．
【题型4 SAS与全等三角形的性质综合应用】
【例4】（23-24·陕西·模拟预测）如图，在△ABC中，AB=AC，过点A作DE∥BC，且AD=AE，求证：CD=BE．
【变式4-1】（23-24八年级·上海·专题练习）如图，在△ABC中，已知点D、E、F分别在边BC、AC、AB上，且FD=ED，BF=CD，∠FDE=∠B，那么∠B和∠C的大小关系如何？为什么？
解：因为∠FDC=∠B+∠DFB ，
即∠FDE+∠EDC=∠B+∠DFB．
又因为∠FDE=∠B（已知），
所以∠ =∠ ．
已知 已知
在△DFB和△EDC中，
所以△DFB≌△EDC ．
因此∠B=∠C．
【变式4-2】（23-24八年级·内蒙古通辽·期中）如图，在△ABC中，∠B=40°，∠C=25°，过点A作AD⊥BC，垂足为D，延长DA至E．使得AE=AC．在边AC上截取AF=AB，连结EF．
(1)求∠EAF的度数．
(2)求证：EF=BC．
【变式4-3】（23-24八年级·河南郑州·期末）如图，四边形ABCD、DEFG都是正方形，连接AE、CG．求证：

(1)AE=CG；
(2)AE⊥CG．
知识点3：由角边角（ASA）证明两个三角形全等
两角和它们的夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”．
用“ASA”来判定两个三角形全等，一定要证明这两个三角形有两个角以及这两个角的夹边分别相等，证明时要加强对夹边的认识．
【题型5 利用ASA证明三角形全等】
【例5】（23-24八年级·河南郑州·期末）如图，∠A=∠B,P为AB的中点，点M为射线AC上（不与点A重合）的任意一点，连接MP，并使MP的延长线交射线BD于点N．试说明：△APM≌△BPN．
【变式5-1】（23-24八年级·湖北武汉·期中）一块三角形玻璃被摔成如图所示的四块，小江想去买一块形状、大小与原来一样的玻璃，但是他只想带去其中的两块，则这两块玻璃的编号可以是（ ）
A．①②B．②④C．③④D．①④
【变式5-2】（23-24八年级·山东枣庄·阶段练习）如图，A、E、F、B在同一条直线上，AE=BF，∠A=∠B，∠CEB=∠DFA，试说明：△AFD≌△BEC．

【变式5-3】（23-24八年级·河南郑州·期末）已知：点B、E、C、F在一条直线上，AB∥DE，AC∥DF，BE=CF．求证：△ABC≌△DEF．

【题型6 ASA与全等三角形的性质综合应用】
【例6】（23-24八年级·云南昭通·阶段练习）如图，AB∥CD，DF=EF，AB=12，CD=9，则AE等于 ．
【变式6-1】（23-24八年级·重庆·期末）如图，某段河流的两岸是平行的，小开想出了一个不用涉水过河就能测得河的宽度的方案，首先在岸边点B处，选对岸正对的一棵树A，然后沿河岸直行20m到达树C，继续前行20m到达点D处，再从点D处沿河岸垂直的方向行走．当到达树A正好被树C遮挡住的点E处时，停止行走，此时DE的长度即为河岸AB的宽度．小开这样判断的依据是（ ）

A．SSS B．SAS C．AAS D．ASA
【变式6-2】（23-24八年级·浙江·期末）如图，在△ABC和△ADE中，点C在边DE上，AB=AD，∠B=∠D，∠1=∠2．
(1)求证：△ABC≌△ADE．
(2)若∠ACB=65°，求∠BCD的度数．
【变式6-3】（23-24八年级·广东佛山·阶段练习）如图，已知AB∥CD，∠ABC,∠BCD的平分线恰好交于AD上一点E，已知AB=2，CD=5，则BC= ．
知识点4：由角角边（AAS）证明两个三角形全等
两角和其中一个角的对边分别相等的两个三角形全等，简写成“角角边”或“AAS”．这一结论很容易由“ASA”推得，将这一结论与“ASA”结合起来，即可得出：两个三角形如果具备两角和一条边对应相等，就可判定其全等．
【题型7 利用AAS证明三角形全等】
【例7】（23-24·陕西西安·八年级·期末）如图，点F在AB上，BC∥AD，AD=AC，∠AED=∠B．求证：△ABC≌△DEA
【变式7-1】（23-24八年级·山西太原·阶段练习）如图，太阳光线AC和A'C'是平行的，在同一时刻，两根高度相等的木杆的影子是一样长的，这利用了全等图形的性质，其中判断△ABC≌△A'B'C'的依据是 ．
【变式7-2】（23-24·山东淄博·八年级·期末）如图， 点E在△ABC的外部，点D在BC上，DE交AC于点F， ∠1=∠2=∠3，AB=AD．求证： △ABC≌△ADE．
【变式7-3】（23-24八年级·安徽合肥期末）如图，在四边形ABCD中，点E在边BC上，∠BAC=∠BCD=∠DAE=90°，AD=AE．求证：△ABE≌△ACD．
【题型8 AAS与全等三角形的性质综合应用】
【例8】（23-24八年级·河南周口·期中）如图，在△ABC中，AD是BC边上的高，BE是AC边上的高，且AD、BE交于点F，若BF=AC,CD=4,BD=10，则线段AF的长为 ．
【变式8-1】（23-24八年级·重庆·期末）在Rt△ABC中，∠BAC=90°，过点A作AD⊥CB于点D，延长DA至点E，使得DE=AC，过点E作EF∥AB，交CB的延长线于点F，连接CE．
(1)求证：△ACB≌△DEF；
(2)若∠FCE=50°，∠CEF=70°，求∠FCA的度数．
【变式8-2】（23-24八年级·上海普陀·期末）如图，已知AB⊥BD，AC⊥CD，∠1=∠2．试说明AD⊥BC的理由．

解：因为AB⊥BD（已知），
所以∠ABD=90°（垂直的意义）．
同理 ．
所以∠ABD=∠ACD（等量代换）．
在△ABD和△ACD中，
∠ABD=∠ACD，∠1=∠2已知，______，
所以△ABD≌△ACD（ ）．
得 （全等三角形的对应边相等）．
又因为∠1=∠2（已知），
所以AD⊥BC（ ）．
【变式8-3】（23-24八年级·陕西西安·阶段练习）如图所示，工人赵师傅用10块高度都是1.5m的相同长方体新型建筑材料，垒了两堵与地面垂直的墙ABCD和EFGH，其中AB⊥BE于点B，FE⊥BE于点E，点P在BE上，已知AP=PF，AB=PE．

(1)求证：△ABP≌△PEF；
(2)求BE的长．
知识点5：由斜边、直角边（HL）证明两个三角形全等
斜边和一条直角边分别相等的两个直角三角形全等，简写成“斜边、直角边”或“HL”．
“HL”定理是直角三角形所独有的，对于一般三角形不成立．
【题型9 利用HL证明三角形全等】
【例9】（23-24八年级·陕西西安·期末）如图，在Rt△ABC和Rt△DEF中，点B、D、C、E在同一条直线上，点C和点E重合．∠B=∠DEF=90°，AB=DE，若添加一个条件后可用“HL”定理证明Rt△ABC≌Rt△DEF，添加的条件是（ ）
A．BC=EFB．∠BCA=∠FC．BA∥EFD．AC=DF
【变式9-1】（23-24八年级·陕西榆林·期中）如图，在四边形ABCD中，AD∥BC，∠A=90°，E是AB上一点，且AD=BE，连接DE、CE，∠1=∠2．求证：△ADE≌△BEC．
【变式9-2】（23-24八年级·云南保山·期末）用三角尺可按下面方法画角平分线：如图摆放使得三角板刻度相同，即PM=PN，画射线OP，则OP平分∠AOB．作图过程用了△OMP≌△ONP，那么△OMP≌△ONP所用的判定定理是（ ）
A．SSSB．AASC．HLD．ASA
【变式9-3】（23-24八年级·山东济南·期末）如图，在△ABC和△A'B'C'中，∠C=∠C'=90°，AB=A'B'，AD与A'D'分别为BC，B'C'边上的中线，且CD=C'D'，求证：△ABC≌△A'B'C'．
【题型10 HL与全等三角形的性质综合应用】
【例10】（23-24八年级·广西贵港·期末）小强在物理课上学习了发声物体的振动试验后，对其作了进一步的探究：在一个支架的横杆点O处用一根细绳悬挂一个小球，小球可以自由摆动，如图，A表示小球静止时的位置，当小强用发声物体靠近小球时，小球从A摆到B位置，此时过点B作BD⊥OA于点D，当小球摆到C位置时，过点C作CE⊥OA于点E，测得OC=20cm,BD=OE=9cm（图中的点A,B,O,C在同一平面内）．

(1)猜想此时OB与OC的位置关系，并说明理由；
(2)求AE的长．
【变式10-1】（23-24八年级·辽宁大连·期末）一天数学课堂上，小明忘记了带圆规，于是他尝试用直角三角板来画角平分线．如图，在∠O的两边上，分别取OA=OB，将两个直角三角板的直角顶点放在点A，B处作OA，OB的垂线，交点为P，一个三角板的斜边与另一个三角板直角边交于点Q，画射线 就得到∠AOB的平分线．
【变式10-2】（23-24八年级·江苏盐城·期末）已知：如图，∠A=∠D=90°，AC=DB．求证：AB=DC．
【变式10-3】（23-24八年级·陕西西安·期中）如图，已知AD是△ABC的高，E为AC上一点，BE交AD于点F，且BF=AC,FD=CD，求∠DBA的度数．