数学八年级上册13.3.2 等边三角形优质学案设计

这是一份数学八年级上册13.3.2 等边三角形优质学案设计，文件包含专题135等边三角形十大题型举一反三人教版原卷版docx、专题135等边三角形十大题型举一反三人教版解析版docx等2份学案配套教学资源，其中学案共79页， 欢迎下载使用。

TOC \ "1-3" \h \u
\l "_Tc31914" 【题型1 利用等边三角形的性质求角的度数】 PAGEREF _Tc31914 \h 1
\l "_Tc21496" 【题型2 利用等边三角形的性质求线段长度】 PAGEREF _Tc21496 \h 2
\l "_Tc8062" 【题型3 利用等边三角形的性质求最值】 PAGEREF _Tc8062 \h 3
\l "_Tc18896" 【题型4 证明等边三角形】 PAGEREF _Tc18896 \h 4
\l "_Tc24731" 【题型5 探究平面直角坐标系中的等边三角形问题】 PAGEREF _Tc24731 \h 6
\l "_Tc26019" 【题型6 探究等边三角形中的折叠问题】 PAGEREF _Tc26019 \h 8
\l "_Tc6725" 【题型7 探究等边三角形中的三角板问题】 PAGEREF _Tc6725 \h 9
\l "_Tc4449" 【题型8 探究等边三角形中的动态问题】 PAGEREF _Tc4449 \h 11
\l "_Tc3193" 【题型9 探究等边三角形中线段或角度之间的关系】 PAGEREF _Tc3193 \h 12
\l "_Tc23449" 【题型10 等边三角形中的多结论问题判断正误】 PAGEREF _Tc23449 \h 14
知识点：等边三角形
（1）定义：三条边都相等的三角形，叫做等边三角形.
（2）等边三角形性质：等边三角形的三个角相等，并且每个角都等于60°.
（3）等边三角形的判定：
①三条边都相等的三角形是等边三角形；
②三个角都相等的三角形是等边三角形；
③有一个角为 60°的等腰三角形是等边三角形.
【题型1 利用等边三角形的性质求角的度数】
【例1】（23-24八年级·黑龙江哈尔滨·期中）如图，D为等边三角形ABC内一点，AD=BD，BP=AB，∠DBP=∠DBC，则∠BPD= 度．
【变式1-1】（23-24八年级·陕西西安·期中）等边三角形两条中线相交所成锐角度数为（ ）
A．30°B．45°C．50°D．60°
【变式1-2】（23-24八年级·福建莆田·期中）如图，△ABC是等边三角形，BC⊥CD，且AC=CD，则∠BAD的度数为（ ）
A．50°B．45°C．40°D．35°
【变式1-3】（23-24八年级·辽宁本溪·期中）如图，△ABC是等边三角形，AD是BC边上的中线，点E在AD上，且DE=12BC，则∠AFE的度数为 ．
【题型2 利用等边三角形的性质求线段长度】
【例2】（23-24八年级·江苏无锡·期中）如图，在等边△ABC中，AC=9，点O在AC上，且AO=3，点P是AB上一动点，连接OP，将线段OP绕点O逆时针旋转60°得到线段OD，若使点D恰好落在BC上，则线段AP的长是（ ）

A．4B．5C．6D．8
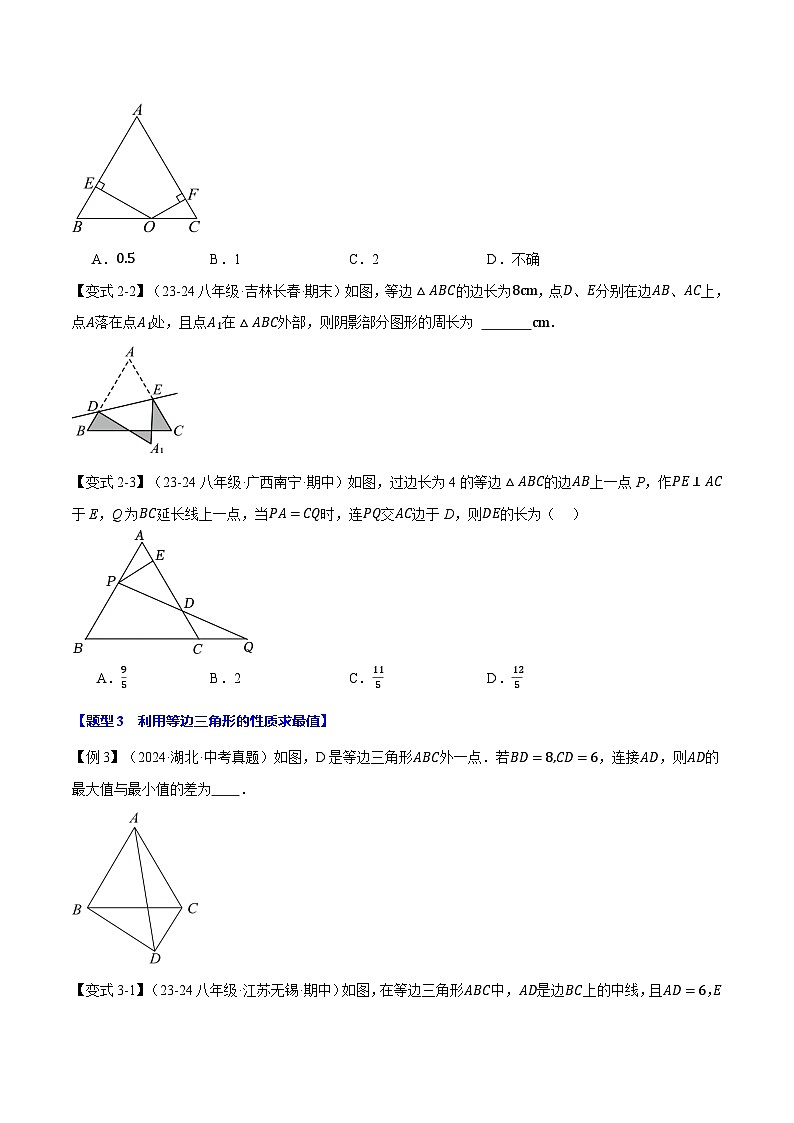
【变式2-1】（23-24八年级·河南漯河·期末）如图，已知等边△ABC，点 O是 BC 上任意一点，OE、OF 分别与两边垂直，等边三角形的高为 1，则 OE+OF 的值为（ ）
A．0.5B．1C．2D．不确
【变式2-2】（23-24八年级·吉林长春·期末）如图，等边△ABC的边长为8cm，点D、E分别在边AB、AC上，点A落在点A1处，且点A1在△ABC外部，则阴影部分图形的周长为 cm．
【变式2-3】（23-24八年级·广西南宁·期中）如图，过边长为4的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（ ）
A．95B．2C．115D．125
【题型3 利用等边三角形的性质求最值】
【例3】（2024·湖北·中考真题）如图，D是等边三角形ABC外一点．若BD=8,CD=6，连接AD，则AD的最大值与最小值的差为 ．
【变式3-1】（23-24八年级·江苏无锡·期中）如图，在等边三角形ABC中，AD是边BC上的中线，且AD=6，E是AD上的一个动点，F是边AB的中点，BE+EF的最小值为（ ）
A．5B．6C．7D．8
【变式3-2】（23-24八年级·福建福州·期中）如图，在等边△ABC中，E是AC边的中点，P是△ABC的中线AD上的动点，且AB=6，则BP-PE的最大值是 ．
【变式3-3】（23-24八年级·福建福州·期中）如图，在△ABC中，∠ACB=90°，BC=6，AC=8，点D是AC边上的中点，点P在BC上的一个动点，连接DP，在DP的下方作等边三角形DPE，连接CE，则CE最小值是（ ）
A．3B．2C．1.5D．1
【题型4 证明等边三角形】
【例4】（23-24八年级·天津宁河·期中）如图所示，在 △ABC中， ∠B=60°，AB=AC，点D，E分别在BC，AB上，且 BD=AE，AD与CE交于点 F．
(1)求证： △ABC是等边三角形；
(2)求证： AD=CE；
(3)求 ∠DFC的大小．
【变式4-1】（23-24八年级·重庆丰都·期末）如图，点E在△ABC的外部，点D在BC上，DE交AC于点F，∠2=∠3，AE=AC，DE=BC．
(1)求证：△ABC≌△ADE．
(2)若∠2=60°，猜想△ABD的形状并证明．
【变式4-2】（23-24八年级·广东广州·阶段练习）在等腰△ABC中，AB=AC=4，∠BAC=120°，AD⊥BC于D，点O、点P分别在射线AD、BA上运动，且保证∠OCP=60°，连接OP．
(1)当点O运动到D点时，如图1，求AP的长度；
(2)当点O运动到D点时，如图1，试判断△OPC的形状并证明；
(3)当点O在射线AD其它地方运动时，△OPC还满足（2）的结论吗？请用图2说明理由．
【变式4-3】（23-24八年级·陕西西安·阶段练习）如图，在四边形ABCD中，∠ABC=∠ADC=90°，AC与BD相交于点E，∠ABD=∠ADB．
(1)填空：AC与BD的位置关系为__________，BE与DE的数量关系为__________；
(2)过点B作BF∥CD交CA的延长线于点F，且AB=AF．
①求证：△BCD是等边三角形；
②若点G，H分别是线段AC，线段CD上的动点，当GH+AH的值最小时，请确定点H的位置，并求出GH与CH之间的数量关系．
【题型5 探究平面直角坐标系中的等边三角形问题】
【例5】（23-24八年级·湖北武汉·期中）在平面直角坐标系中，点A的坐标为0,4
(1)如图1，若点B的坐标为3,0，△ABC是等腰直角三角形，BA=BC，∠ABC=90°，求C点坐标；
(2)如图2，若点E是AB的中点，求证：AB=2OE；
(3)如图3，△ABC是等腰直角三角形，BA=BC，∠ABC=90°，△ACD是等边三角形，连接OD，若∠AOD=30°，求B点坐标
【变式5-1】（23-24八年级·辽宁锦州·期末）如图，在平面直角坐标系中，边长为1的正方形A1B1C1D1（记为第1个正方形）的顶点A1与原点重合，点B1在y轴上，点D1在x轴上，点C1在第一象限内，以C1为顶点作等边△C1A2B2，使得点A2落在x轴上，A2B2⊥x轴，再以A2B2为边向右侧作正方形A2B2C2D2（记为第2个正方形），点D2在x轴上，以C2为顶点作等边△C2A3B3，使得点A3落在x轴上，A3B3⊥x轴，若按照上述的规律继续作正方形，则第2021个正方形的边长为 ．
【变式5-2】（23-24八年级·黑龙江齐齐哈尔·期末）如图，在平面直角坐标系中，△AOP为等边三角形，A点坐标为(0，1)，点B在y轴上且位于A点上方，以BP为边向BP的右侧作等边△PBC，连接CA，并延长CA交x轴于点E．
(1)求证：OB=AC；
(2)判断AP是否平分∠OAC？请说明理由；
(3)在y轴上是否存在点Q，使得△AEQ为等腰三角形？若存在，请直接写出满足条件的所有点Q的坐标；若不存在，请说明理由．
【变式5-3】（23-24八年级·天津和平·期末）如图，在平面直角坐标系中，O为原点，等边△ABC的顶点A，B在x轴上，顶点C的坐标为(0,12)，∠BAC的平分线交y轴于点D．

(1)如图①，求点D坐标；
(2)如图②，E为x轴上一点，以CE为边，在第一象限内作等边△CEF，连接FB并延长交y轴于点G．求OG的长；
(3)如图③，在（1）的条件下，M为y轴正半轴上D点上方的任意一点，在BM右上方作∠BMN=60°交AD延长线于N点，求证：DN-DM是定值．
【题型6 探究等边三角形中的折叠问题】
【例6】（23-24八年级·广西贺州·期末）如图，等边△ABC边长为3，点D为AB边上的一动点（D不与A、B重合）．过点A折叠△ABC，使点B与C重合，得折痕AF交BC于F，然后展开；再过点D折叠△ABC，折痕DE交AC于点E，使点A落在折痕AF所在的直线上，记为点P，两折痕AF与DE交于点O．
(1)求证：DE∥BC；
(2)点D在运动过程中，△ADE始终是等边三角形吗？请说明理由；
(3)连接DP、BP，当△BDP为直角三角形时，求AD的长．
【变式6-1】（23-24八年级·河北廊坊·期末）如图1，△ABD是等边三角形，点P为射线AB上一动点，连接DP，作∠DPE=∠DAB=60°，PE交射线DA于点E，点O是线段AE，PE垂直平分线的交点．
（1）当点O在AB边上时，∠ADP=______．
（2）①当点P，B重合时，作AO'⊥DE，交PE的垂直平分线于点O'，则∠O'PD=______．
②当点P在线段AB上，或AB的延长线上时，∠OPD的度数是否为定值？若是，请写出这个数，并选择点P在线段AB上时，通过计算进行说明；若不是，请说明理由．
（3）如图2，把等边三角形△ABD沿着BD折叠，得到△BDC，且点A落在点C处，连接AC．当PE//AC时，证明AP平分∠DPE，并在△DPE内确定一点T，使点T到△DPE三边的距离相等（不写作法，只保留作图痕迹）．
【变式6-2】（23-24八年级·广东中山·期末）已知△ABC中，∠B= 60°，点D是AB边上的动点，过点D作DE∥BC交AC于点E，将△ABE沿DE折叠，点A对应点为F点.
(1)如图1，当点F恰好落在BC边上，求证：△BDF是等边三角形；
(2)如图2，当点F恰好落在△ABC内，且DF的延长线恰好经过点C，CF=EF，求∠A的大小；
(3)如图3，当点F恰好落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB=9，求BG的长.
【变式6-3】（23-24八年级·河南省直辖县级单位·期末）在学习完等腰三角形之后，某兴趣小组开展了如下数学活动：如图，正方形纸片ABCD，①先对折使AB与CD重合，得到折痕EF；②折叠纸片，使得点A落在EF的点H上，沿BH和CH剪下△BCH，小组成员得到了如下结论：①∠BHF=30°；②BF=12CH；③△BCH是等边三角形；④∠ABG=15°；⑤四边形ABHE和四边形DCHE全等．正确的个数是（ ）

A．2个B．3个C．4个D．5个
【题型7 探究等边三角形中的三角板问题】
【例7】（23-24八年级·河北保定·期中）如图，在等边△ABC中，AB=10，将含30°角的三角板中60°角的顶点D放在边AB上移动，使这个60°角的两边与△ABC的边AC，BC分别交于点E，F，且DE始终与AB垂直，连接EF．
(1)△BDF是什么三角形？请说明理由．
(2)如图1，若AE=8，求CF的长．
(3)如图2，当EF∥AB时，求AE的长．
【变式7-1】（23-24八年级·辽宁沈阳·期末）将含30°角的直角三角板和直尺按如图所示的方式放置，已知∠α=60°，点B，点C表示的刻度分别为1cm,3cm，则△ABC的周长为 cm．
【变式7-2】（23-24八年级·安徽铜陵·阶段练习）如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=1．将三角板中30°角的顶点D放在AB边上移动，使这个30°角的两边分别与△ABC的边AC，BC相交于点E，F，且使DE始终与AB垂直．
(1)求证：△BDF是等边三角形；
(2)求AD-CF的值．
【变式7-3】（23-24八年级·江苏徐州·期末）如图①，已知∠AOB=120°，OC平分∠AOB．将直角三角板如图放置，使直角顶点D在OC上，60°角的顶点E在OB上，斜边与OA交于点F（F与O不重合），连接DF．
(1)如图②，若DE⊥OB，求证：△DEF为等边三角形．
(2)如图③，求证：OD=OE+OF．
【题型8 探究等边三角形中的动态问题】
【例8】（23-24八年级·山东枣庄·开学考试）如图，△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，
(1)当点P的运动速度是1cm/s，点Q的运动速度是2cm/s，当Q到达点C时，设运动时间为t（s），当t=2时，判断△BPQ的形状，并说明理由；
(2)当它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t（s），则当t为何值时，△PBQ是直角三角形？
【变式8-1】（23-24八年级·河北廊坊·期末）如图，△ABC中，AB=BC=AC=12cm，现有两点M、N分别从点A、点B同时出发，沿三角形的边运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次到达B点时，M、N同时停止运动．点M、N运动（ ）s后，可得到等边△AMN．
A．3B．4C．5D．不能确定
【变式8-2】（23-24八年级·广东江门·期中）已知，如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=18cm．动点P从点A出发，沿AB向点B运动，动点Q从点B出发，沿BC向点C运动，如果动点P以2cm/s，Q以1cm/s的速度同时出发，设运动时间为ts，解答下列问题：
(1)AB= ．
(2)求当△PBQ是等边三角形时对应的t值？
(3)P，Q在运动过程中，△PBQ的形状不断发生变化，当t为何值时，△PBQ是直角三角形？说明理由．
【变式8-3】（23-24八年级·广东湛江·期末）如图，在△ABC中，∠B=60°，点M从点B出发沿射线BC方向，在射线BC上运动．在点M运动的过程中，连结AM，并以AM为边在射线BC上方，作等边△AMN，连结CN．

(1)当∠BAM=__________°时，AB=2BM；
(2)请添加一个条件：__________，使得△ABC为等边三角形；
(3)在（2）的条件下，当△ABC为等边三角形时，求证：CN+CM=AC；
【题型9 探究等边三角形中线段或角度之间的关系】
【例9】（23-24八年级·广东广州·期末）如图1，△ABC是等边三角形，D为AC边上一点，连接BD，点C关于BD的对称点为点E，连接BE．
(1)若AB是∠DBE的平分线，求∠ABD的度数；
(2)如图2，连接EA并延长交BD的延长线于点F，
①求∠F的度数；
②探究EA，AF和BF三者之间满足的等量关系，并说明理由．
【变式9-1】（23-24八年级·贵州毕节·期末）如图，在等边△ABC中，∠ABC与∠ACB的平分线交于点D，分别作BD，CD的垂直平分线EM，FN，分别交BC于点M，N，则MN与△ABC边长的关系是（ ）
A．MN=12BCB．MN=13BC
C．MN=14BCD．无法确定其倍比关系
【变式9-2】（23-24八年级·河南洛阳·期末）如图，将长方形纸片ABCD对折，使AD与BC重合，展平纸片，得到折痕EF；折叠纸片，使点B落在EF上，并使折痕经过点A，得到折痕AM，点B，E的对应点分别为G，H，展平纸片，连结BG，BH，则∠ABH与∠GAM的关系是 ．
【变式9-3】（23-24八年级·重庆綦江·期末）如图，△ABC是等边三角形，点D在边AC上（点D不与点A，C重合），点E是射线BC上的一个动点（点E不与点B，C重合），连接DE，以DE为边作等边△DEF，连接CF.
（1）如图1，当DE的延长线与AB的延长线相交，且点C，F在直线DE的同侧时，过点D作DG∥AB，DG交BC于点G，求证：CF=EG；
（2）如图2，当DE的反向延长线与AB的反向延长线相交，且点C，F在直线DE的同侧时，求证：CD=CE+CF；
（3）如图3，当DE的反向延长线与线段AB相交，且点C，F在直线DE的异侧时，猜想CD、CE、CF之间的等量关系，并说明理由.
【题型10 等边三角形中的多结论问题判断正误】
【例10】（23-24八年级·广东深圳·期末）如图，C为线段AE上一动点（不与A、E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，以下五个结论：①AD=BE；②PQ∥AE；③CP=CQ；④BO=OE；⑤∠AOB=60°，恒成立的结论有（ ）

A．①③⑤B．①③④⑤C．①②③⑤D．①②③④⑤
【变式10-1】（23-24八年级·广东佛山·期中）如图，△ABC是等边三角形，△ABD是等腰直角三角形，∠BAD=90°，AE⊥BD于点E，连接CD，分别交AE、AB于点F、G，过点A作AH⊥CD交BD于点H，EH=1，则下列结论：①∠ACD=15°；②△AFG是等腰三角形；③△ADF≌△BAH；④DF=2．其中正确的有（ ）
A．①②③B．①②④C．①③④D．②③④
【变式10-2】（2024·山东泰安·模拟预测）如图，等边△ABC中，AB=2，D为△ABC内一点，且DA=DB，E为△ABC外一点，BE=AB且∠EBD=∠CBD，连接DE、CE，则下列结论：①∠DAC=∠DBC；②BE⊥AC；③∠DEB=30°；④若EC∥AD，则S△EBC=1，其中正确的有（ ）
A．1个B．2个C．3个D．4个
【变式10-3】（23-24八年级·重庆璧山·期中）如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于点M，连接BM；下列结论：①AP=CE；②∠PME=60°；③BM平分∠AME；④AM+MC=BM，其中正确的有（ ）
A．1个B．2个C．3个D．4个