

数学七年级上册(2024)6.2 角教学演示课件ppt
展开1.会用量角器度量角后比长短,会用“叠合法” 比较角的大小,会用尺规法作一个角等于已知角.2.了解角的平分线的定义,并能够利用量角器画一个已知角的平分线;3.会比较角的大小,能运用角的平分线意义进行简单的计算,发展学生有条理的思考并能表述。重点:角的平分线的概念,利用角的平分线的意义 进行简单的计算.难点:有条理的思考,并能表述能力.
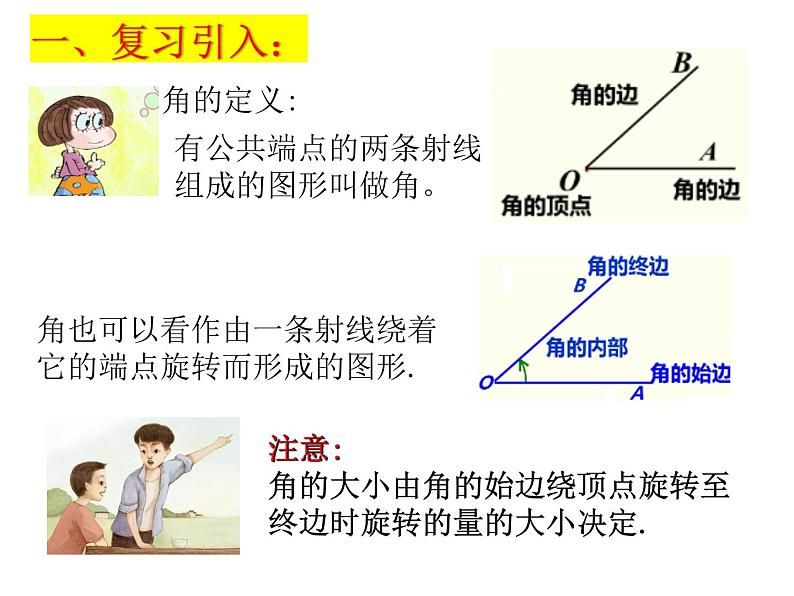
有公共端点的两条射线组成的图形叫做角。
角也可以看作由一条射线绕着它的端点旋转而形成的图形.
注意:角的大小由角的始边绕顶点旋转至终边时旋转的量的大小决定.
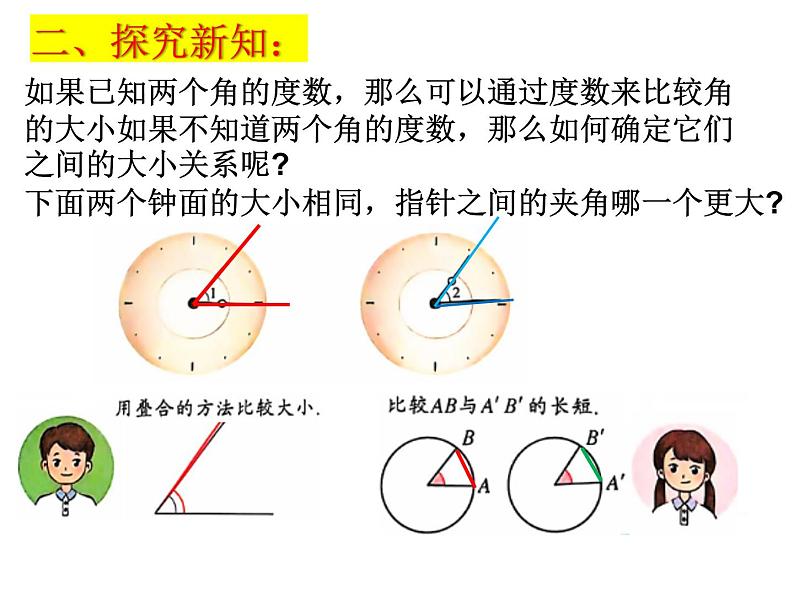
如果已知两个角的度数,那么可以通过度数来比较角的大小如果不知道两个角的度数,那么如何确定它们之间的大小关系呢?
下面两个钟面的大小相同,指针之间的夹角哪一个更大?
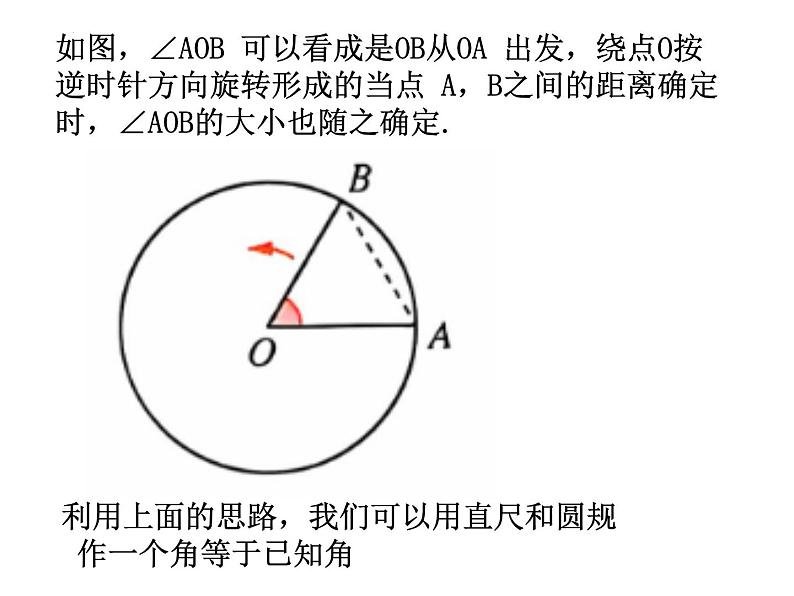
如图,∠AOB 可以看成是OB从OA 出发,绕点O按逆时针方向旋转形成的当点 A,B之间的距离确定时,∠AOB的大小也随之确定.
利用上面的思路,我们可以用直尺和圆规 作一个角等于已知角
BO A
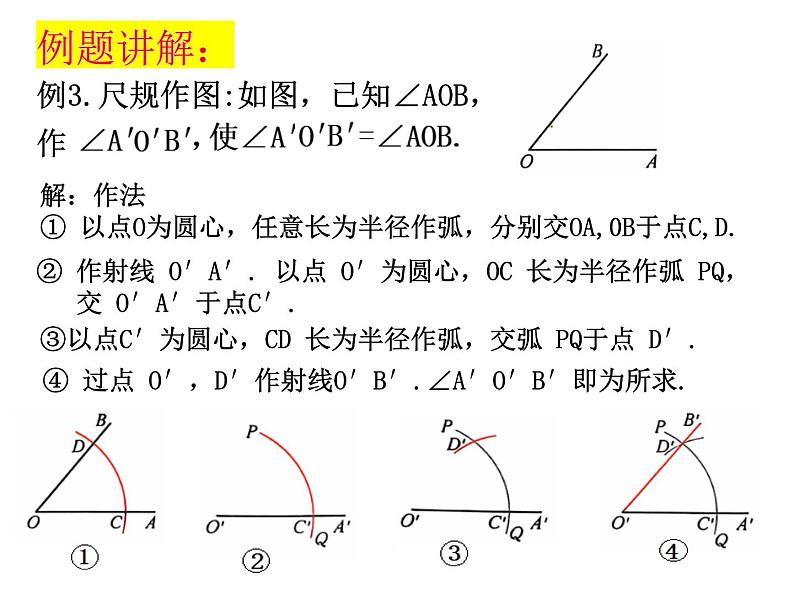
④ 过点 O′,D′作射线O′B′.∠A′O′B′即为所求.
例3.尺规作图:如图,已知∠AOB,作
解:作法① 以点O为圆心,任意长为半径作弧,分别交OA,0B于点C,D.
② 作射线 O′A′. 以点 O′为圆心,OC 长为半径作弧 PQ, 交 O′A′于点C′.
③以点C′为圆心,CD 长为半径作弧,交弧 PQ于点 D′.
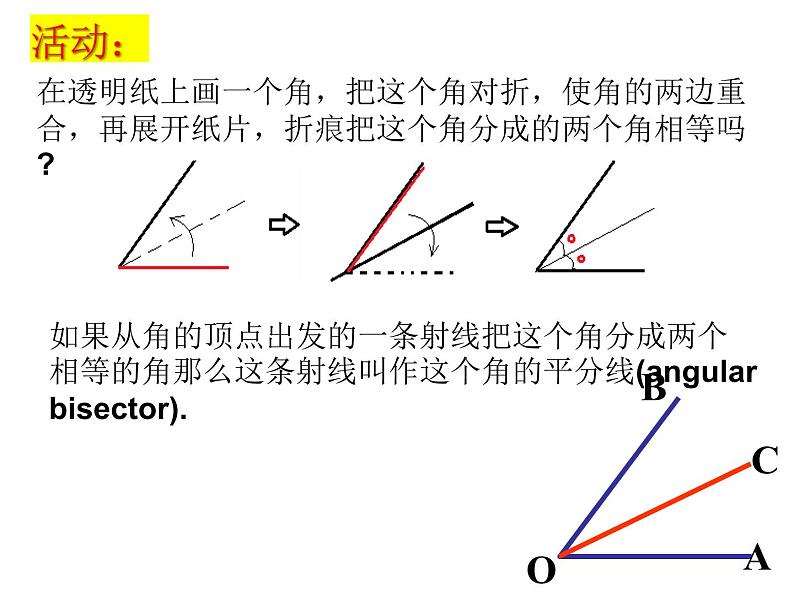
在透明纸上画一个角,把这个角对折,使角的两边重合,再展开纸片,折痕把这个角分成的两个角相等吗?
如果从角的顶点出发的一条射线把这个角分成两个相等的角那么这条射线叫作这个角的平分线(angular bisectr).
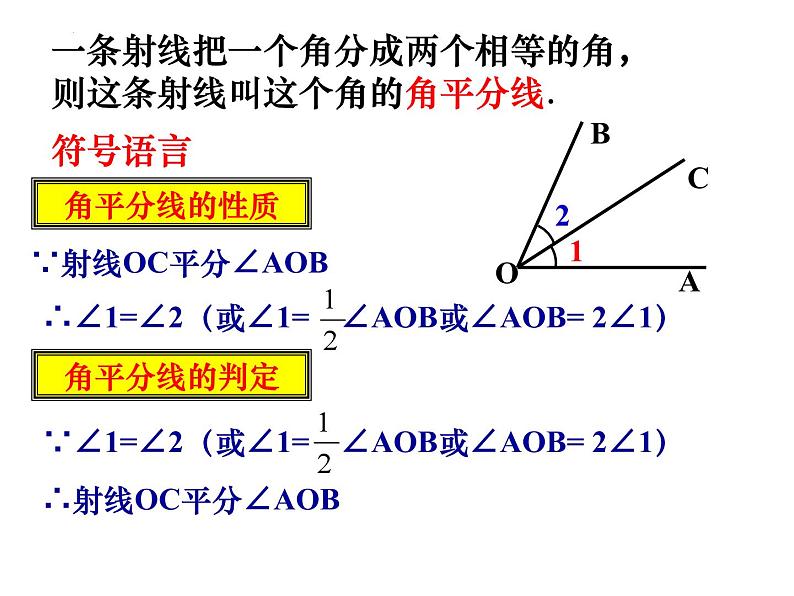
一条射线把一个角分成两个相等的角,则这条射线叫这个角的角平分线.
∵射线OC平分∠AOB
∴∠1=∠2(或∠1= ∠AOB或∠AOB= 2∠1)
∴射线OC平分∠AOB
∵∠1=∠2(或∠1= ∠AOB或∠AOB= 2∠1)
例4、如图,∠AOD-80°,OB是/AOC的平分线, ∠AOB-30°.求∠AOC,∠COD 的大小。
所以∠COD=80°-60°-20°
解:因为OB是∠AOC 的平分线,∠AOB=30°,
所以∠AOC=2∠AOB=2×30°=60°
又因为∠COD=∠AOD-∠AOC,∠AOD=80°,
如图,射线OC从∠AOB 的边 OA出发,绕点 O向边OB 旋转,∠1和∠2的大小关系发生了怎样的变化?
对于任意的∠α和∠β,下列三种关系中有且只有一种成立:∠a<∠β ,∠a=∠β,∠a>∠β.
1.下列度数的角中,利用一副直角三角尺不能画出的是( ) A. 105° B. 75° C.130° D.15°
2.将长方形纸片ABCD沿AE折叠,得到如图所示的图形, 若∠CED′=50°,则∠AED 的度数为( ) A.50° B.60° C.65° D.70°
3.如图,∠AOB=130°,OC是∠AOB 内部任意一条射线,OD,OE分别是∠AOC,∠BOC的平分线,下列叙述正确的是( )A.∠DOE的度数不能确定 B.∠AOD= ∠EOCC.∠AOD+∠BOE=65°D.∠BOE=2∠COD
4.如图(1),打台球时,一般情况下球的反射角等于入射角请估测图(2)中哪个角是反射角,并判断∠EOA∠EOB,∠EOC,∠EOD之间的大小关系.
5.如图,O是直线AB上的一点,OD平分∠BOC, ∠DOE=∠AOC=30°求/BOE的大小.
8.如图,∠AOB:∠BOC=3:2,0D是∠BOC的平分线, OE是∠AOC的平分线,∠BOE=12°,求∠DOE的度数。
2、掌握角的平分线的定义,并能够利用量角器 画一个已知角的平分线,运用角的平分线的 性质进行说理和计算;
1、会用量角器、三角尺与圆规、直尺画一个角 等于已知角,并比较它们的区别与联系;
3、会运用反射角等于入射角进行说理、计算。
1.如图,OE平分∠AOB,射线OC在∠AOE内,∠BOC=2∠AOC, 若∠AOB=114°,则∠COE的度数为( ) A.18° B.19° C.20° D.21°
2.如图,已知∠AOC=90°,∠COB= ,OD平分∠AOB, 则∠COD 的度数为 ( ) A. B.45°- C.45°- D.90°-
3.已知∠AOB=60°,射线OC平分∠AOB.若以OC为一边 画∠COP=15°,则∠BOP 的度数为 ( )A. 15° B.45° C.15°或 30° D.15°或 45°
4.如图,直线 AB,CD相交于点O,∠2-∠1=15°, ∠3=130°,(1)求∠2的度数;(2)试说明:OE是∠COB的平分线.
初中数学苏科版(2024)七年级上册(2024)2.5 有理数的乘法与除法教课内容ppt课件: 这是一份初中数学苏科版(2024)七年级上册(2024)<a href="/sx/tb_c4050030_t3/?tag_id=26" target="_blank">2.5 有理数的乘法与除法教课内容ppt课件</a>,共18页。PPT课件主要包含了学习目标,复习旧知,有理数的乘法法则,有理数乘法运算律,倒数的概念,探究活动,讲授新课,例题分析,练习巩固,归纳总结等内容,欢迎下载使用。
湘教版(2024)七年级上册(2024)4.3 角说课ppt课件: 这是一份湘教版(2024)七年级上册(2024)<a href="/sx/tb_c4049370_t3/?tag_id=26" target="_blank">4.3 角说课ppt课件</a>,文件包含431角与角的大小比较pptx、角的概念mp4等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
数学七年级上册6.2 角教案配套课件ppt: 这是一份数学七年级上册<a href="/sx/tb_c4050052_t3/?tag_id=26" target="_blank">6.2 角教案配套课件ppt</a>,共48页。PPT课件主要包含了角的定义,练习1计算,教材延伸方向角,补角和余角的概念等内容,欢迎下载使用。














