2025届陕西省定边县联考九上数学开学考试模拟试题【含答案】

这是一份2025届陕西省定边县联考九上数学开学考试模拟试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图所示，在平行四边形中，对角线相交于点，，，，则平行四边形的周长为（ ）
A．B．
C．D．
2、（4分）一个直角三角形斜边上的中线为5，斜边上的高为4，则此三角形的面积为（ ）
A．25B．16C．20D．10
3、（4分）正方形具有而菱形不一定具有的性质是( )
A．对角线互相垂直B．对角线相等C．对角线互相平分D．对角相等
4、（4分）若关于x的一元二次方程的两个根为x1=1，x2=2，则这个方程可能是（ ）
A．x2-3x+2=0B．x2+3x+2=0C．x2+3x-2=0D．x2-2x+3=0
5、（4分）已知四边形ABCD中，AB∥CD，对角线AC与BD交于点O，下列条件中不能用作判定该四边形是平行四边形条件的是（ ）
A．AB=CDB．AC=BDC．AD∥BCD．OA=OC
6、（4分）在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，则AB的长为( )
A．3B．4C．5D．6
7、（4分）如图，点P是∠AOB的角平分线上一点，过点P作PC⊥OA于点C，且PC=3，则点P到OB的距离为（ ）
A．3B．4C．5D．6
8、（4分）如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（ ）
A．20B．24C．40D．48
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，点A、B、C、D分别是“蛋圆”与坐标轴的交点，AB为半圆的直径，且抛物线的解析式为，则半圆圆心M的坐标为______．
10、（4分）已知菱形的两条对角线长分别为1和4，则菱形的面积为______．
11、（4分）若一次函数的函数值随的增大而增大，则的取值范围是_____.
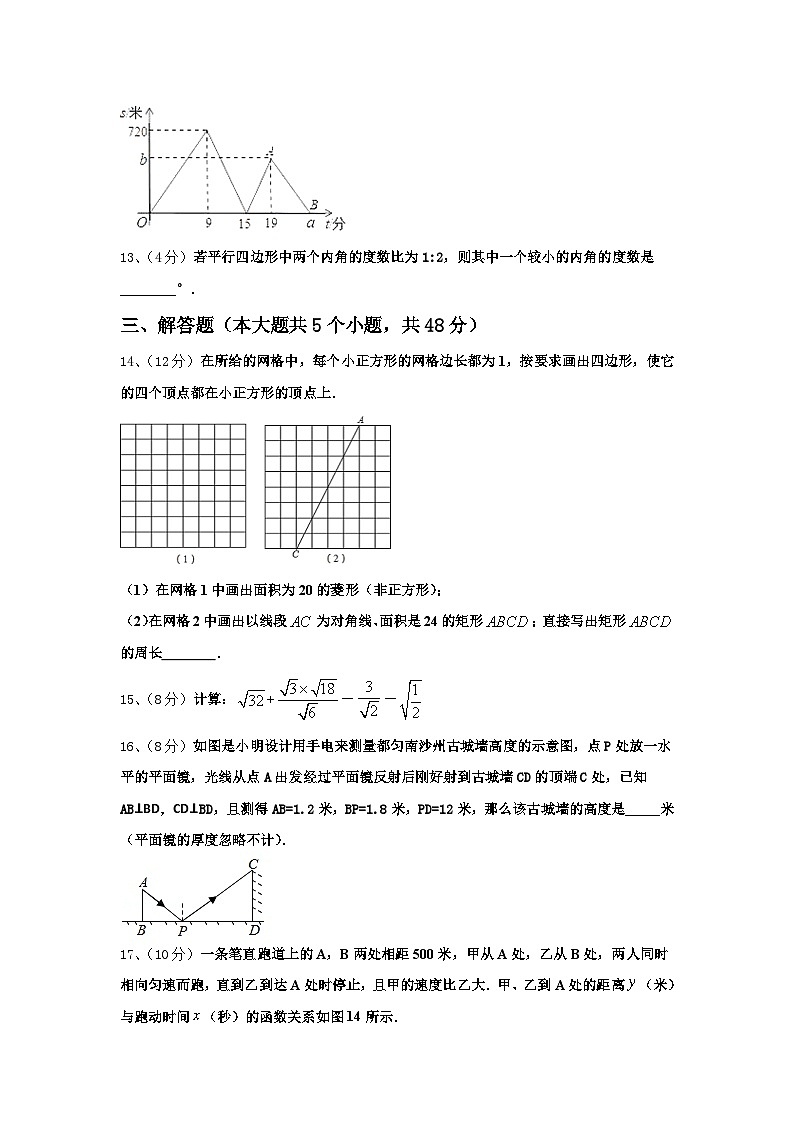
12、（4分）甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示。下列说法：①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是___(填序号).
13、（4分）若平行四边形中两个内角的度数比为1:2，则其中一个较小的内角的度数是________°．
三、解答题（本大题共5个小题，共48分）
14、（12分）在所给的网格中，每个小正方形的网格边长都为1，按要求画出四边形，使它的四个顶点都在小正方形的顶点上．
（1）在网格1中画出面积为20的菱形（非正方形）；
（2）在网格2中画出以线段为对角线、面积是24的矩形；直接写出矩形的周长 ．
15、（8分）计算：+－－
16、（8分）如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米，那么该古城墙的高度是_____米（平面镜的厚度忽略不计）．
17、（10分）一条笔直跑道上的A，B两处相距500米，甲从A处，乙从B处，两人同时相向匀速而跑，直到乙到达A处时停止，且甲的速度比乙大．甲、乙到A处的距离（米）与跑动时间（秒）的函数关系如图14所示．
（1）若点M的坐标（100，0），求乙从B处跑到A处的过程中与的函数解析式；
（2）若两人之间的距离不超过200米的时间持续了40秒．
①当时，两人相距200米，请在图14中画出P（，0）．保留画图痕迹，并写出画图步骤；
②请判断起跑后分钟，两人之间的距离能否超过420米，并说明理由．
18、（10分）直线是同一平面内的一组平行线．
(1)如图1．正方形的4个顶点都在这些平行线上，若四条直线中相邻两条之间的距离都是1，其中点，点分别在直线和上，求正方形的面积；
(2)如图2，正方形的4个顶点分别在四条平行线上，若四条直线中相邻两条之间的距离依次为．
①求证：；
②设正方形的面积为，求证．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知矩形，给出三个关系式：①②③如果选择关系式__________作为条件（写出一个即可），那么可以判定矩形为正方形，理由是_______________________________ .
20、（4分）如果关于x的方程有实数根，则m的取值范围是_______________．
21、（4分）如图，在平面直角坐标系中，菱形ABCD的顶点A在x轴负半轴上，顶点B在x轴正半轴上．若抛物线p=ax2-10ax+8（a＞0）经过点C、D，则点B的坐标为________．
22、（4分）如图，矩形纸片中，已知，，点在边上，沿折叠纸片，使点落在点处，连结，当为直角三角形时，的长为______.
23、（4分）如果正比例函数的图象经过点（1，－2），那么k 的值等于 ▲ ．
二、解答题（本大题共3个小题，共30分）
24、（8分）平面直角坐标系中，设一次函数的图象是直线.
（1）如果把向下平移个单位后得到直线，求的值；
（2）当直线过点和点时，且，求的取值范围；
（3）若坐标平面内有点，不论取何值，点均不在直线上，求所需满足的条件.
25、（10分）如图所示，有一条等宽的小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，则这条小路的面积是多少？
26、（12分）已知（如图），点分别在边上，且四边形是菱形
（1）请使用直尺与圆规，分别确定点的具体位置（不写作法，保留画图痕迹）；
（2）如果，点在边上，且满足，求四边形的面积；
（3）当时，求的值。
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
由▱ABCD的对角线AC，BD相交于点O，AE=EB，易得DE是△ABC的中位线，即可求得BC的长，继而求得答案．
【详解】
∵▱ABCD的对角线AC，BD相交于点O，
∴OA=OC，AD=BC，AB=CD=5，
∵AE=EB，OE=3，
∴BC=2OE=6，
∴▱ABCD的周长=2×（AB+BC）=1．
故选：D．
此题考查了平行四边形的性质以及三角形中位线的性质．注意证得DE是△ABC的中位线是关键．
2、C
【解析】
根据直角三角形的性质可得出斜边的长，进而根据三角形的面积公式求出此三角形的面积．
【详解】
解：根据直角三角形斜边上的中线等于斜边的一半知：此三角形的斜边长为5×2=10；
所以此三角形的面积为：×10×4=1．
故选：C．
本题考查直角三角形的性质以及三角形的面积计算方法．掌握直角三角形中，斜边上的中线等于斜边的一半是解题的关键．
3、B
【解析】
根据正方形的性质以及菱形的性质逐项进行分析即可得答案.
【详解】
菱形的性质有①菱形的对边互相平行，且四条边都相等，②菱形的对角相等，邻角互补，③菱形的对角线分别平分且垂直，并且每条对角线平分一组对角；
正方形具有而菱形不一定具有的性质是矩形的特殊性质(①矩形的四个角都是直角，②矩形的对角线相等)，
A．菱形和正方形的对角线都互相垂直，故本选项错误；
B．菱形的对角线不一定相等，正方形的对角线一定相等，故本选项正确；
C．菱形和正方形的对角线互相平分，故本选项错误；
D．菱形和正方形的对角都相等，故本选项错误，
故选B.
本题考查了正方形与菱形的性质，解题的关键是熟记正方形与菱形的性质定理．
4、A
【解析】
先计算出x1+x2=3，x1x2=2，然后根据根与系数的关系得到满足条件的方程可为x2-3x+2=1．
【详解】
解：∵x1=1，x2=2，
∴x1+x2=3，x1x2=2，
∴以x1，x2为根的一元二次方程可为x2-3x+2=1．
故选A．
本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=1（a≠1）的两根时，x1+x2=−，x1x2=．
5、B
【解析】
A. AB=CD,一组对边平行且相等的四边形是平行四边形；
B. AC=BD，一组对边平行，另一组对边相等的四边形不一定是平行四边形，也可能是等腰梯形；
C. AD∥BC，两组对边分别平行的四边形是平行四边形；
D. OA=OC，通过证明两个三角形全等，得出AB=CD,可以得出平行四边形.故选B.
6、C
【解析】
∠C＝90°，AC＝3，BC＝4,,
所以AB=5.故选C.
7、A
【解析】
过点P作PD⊥OB于D，根据角平分线上的点到角的两边距离相等可得PC=PD，从而得解．
【详解】
解：如图，过点P作PD⊥OB于D，
∵点P是∠AOB的角平分线上一点，PC⊥OA，
∴PC=PD=1，即点P到OB的距离等于1．
故选：A．
本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．
8、A
【解析】
分析：由菱形对角线的性质，相互垂直平分即可得出菱形的边长，菱形四边相等即可得出周长．
详解：由菱形对角线性质知，AO=AC=3，BO=BD=4，且AO⊥BO，
则AB==5，
故这个菱形的周长L=4AB=1．
故选A．
点睛：本题考查了菱形面积的计算，考查了勾股定理在直角三角形中的运用，考查了菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键，难度一般．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（1，0）．
【解析】
当y=0时，，解得：x1=﹣1，x2=3，故A（﹣1，0），B（3，0），则AB的中点为：（1，0）．
故答案为（1，0）．
10、1
【解析】
利用菱形的面积等于对角线乘积的一半求解．
【详解】
解：菱形的面积=×1×4=1．
故答案为1．
本题考查了菱形的性质：熟练掌握菱形的性质（菱形具有平行四边形的一切性质； 菱形的四条边都相等； 菱形的两条对角线互相垂直，并且每一条对角线平分一组对角）． 记住菱形面积=ab（a、b是两条对角线的长度）．
11、k＞2
【解析】
试题分析：本题主要考查一次函数的性质，掌握一次函数的性质是解题的关键，即在y=kx+b中，当k＞0时y随x的增大而增大，当k＜0时y随x的增大而减小.
【详解】
根据题意可得：k－2＞0，解得：k＞2.
考点：一次函数的性质；一次函数的定义
12、①②③.
【解析】
根据甲步行720米，需要9分钟，进而得出甲的运动速度，利用图形得出乙的运动时间以及运动距离，进而分别判断得出答案．
【详解】
由图象得出甲步行720米，需要9分钟，
所以甲的运动速度为：720÷9=80(m/分)，
当第15分钟时,乙运动15−9=6(分钟)，
运动距离为：15×80=1200(m)，
∴乙的运动速度为：1200÷6=200(m/分)，
∴200÷80=2.5,(故②正确)；
当第19分钟以后两人之间距离越来越近,说明乙已经到达终点,则乙先到达青少年宫,(故①正确)；
此时乙运动19−9=10(分钟)，
运动总距离为：10×200=2000(m)，
∴甲运动时间为：2000÷80=25(分钟)，
故a的值为25,(故④错误)；
∵甲19分钟运动距离为：19×80=1520(m)，
∴b=2000−1520=480,(故③正确).
故正确的有：①②③.
故答案为：①②③.
此题考查一次函数的应用，解题关键在于结合函数图象进行解答.
13、60°
【解析】
根据平行四边形的性质得出，推出，根据，求出即可.
【详解】
四边形是平行四边形，
，
，
，
.
故答案为：.
本题考查了平行线的性质和平行四边形的性质的应用，能熟练地运用性质进行计算是解此题的关键，题目比较典型，难度不大.
三、解答题（本大题共5个小题，共48分）
14、（1）见解析；（2）
【解析】
（1）根据边长为5，高为4的菱形面积为20作图即可；
（2）边长为和的矩形对角线AC长为，面积为24，据此作图即可．
【详解】
解：（1）如图1所示，菱形即为所求；
（2）如图2所示，矩形即为所求．
∵，
∴矩形的周长为．
故答案为：．
本题考查的知识点是菱形的性质以及作图，根据题意计算得出菱形的边长和矩形的边长是解此题的关键．
15、2+3
【解析】
根据二次根式的运算法则即可求出答案．
【详解】
原式＝4+3﹣﹣ ＝2+3
本题考查二次根式的运算，解题的关键是熟练运用二次根式的运算，本题属于基础题型．
16、1
【解析】
试题分析：由题意知：光线AP与光线PC，∠APB=∠CPD，∴Rt△ABP∽Rt△CDP，∴，∴CD==1（米）．故答案为1．
考点：相似三角形的应用．
17、（1）；（2）①见解析；②起跑后分钟，两人之间的距离不能超过米，理由见解析．
【解析】
（1）设乙从B处跑到A处的过程中y与x的函数关系式为y=kx+b，把（0，10）和（100，0）代入求出k，b的值即可，
（2）①设，两直线相交于点.过点作轴的垂线，交直线于点，
在射线上截取，使过点作轴的垂线，则垂足即为所求点．
②由两人有相距200到相遇用时1秒，由a＞b，，起跑后分钟(即秒)，两人处于相遇过后，但乙未到达处，则计算乙在90秒内离开B距离比较即可．
【详解】
（1）设
把分别代入，可求得
∴解析式为
（2）如图：
设，两直线相交于点.
步骤为: ．
①过点作轴的垂线，交直线于点
②在射线上截取，使
③过点作轴的垂线，则垂足即为所求点．
（3）起跑后分钟，两人之间的距离不能超过米．
理由如下：
由题可设
∵两人之间的距离不超过米的时间持续了秒，
∴可设当或时，两人相距为米．
∴相遇前，当时，，即
也即①．
相遇后，当时，
即
也即②．
把①代入②，可得
解得
当两人相遇时，，即
即，解得x=1．
∵甲的速度比乙大，所以，可得
∴起跑后分钟(即秒)，两人处于相遇过后，但乙未到达处．
∴两人相距为
∵，
∴两人之间的距离不能超过米.
本题为一次函数图象问题，考查了一次函数图象性质、方程和不等式有关知识，解答关键是根据条件构造方程或不等式解决问题．
18、（1）9或5；（2）①见解析，②见解析
【解析】
（1）分两种情况：①如图1-1，得出正方形ABCD的边长为2，求出正方形ABCD的面积为9；
②如图1-2，过点B作EF⊥l1于E，交l4于F，则EF⊥l4，证明△ABE≌△BCF（AAS），得出AE=BF=2由勾股定理求出AB=，即可得出答案；
（2）①过点B作EF⊥l1于E，交l4于F，作DM⊥l4于M，证明△ABE≌△BCF（AAS），得出AE=BF，同理△CDM≌△BCF（AAS），得出△ABE≌△CDM（AAS），得出BE=DM即可；
②由①得出AE=BF=h2+h2=h2+h1，得出正方形ABCD的面积S=AB2=AE2+BE2，即可得到答案.
【详解】
解：（1）①如图，当点分别在上时，面积为：；
②如图，当点分别在上时，过点B作EF⊥l1于E，交l4于F，则EF⊥l4，
∵四边形ABCD是正方形，
∴AB=BC，∠ABC=90°，
∴∠ABE+∠CBF=180°-90°=90°，
∵∠CBF+∠BCF=90°，
∴∠ABE=∠BCF，
在△ABE和△BCF中
，
∴△ABE≌△BCF（AAS），
∴AE=BF=2，
∴AB=，
∴正方形ABCD的面积=AB2=5；
综上所述，正方形ABCD的面积为9或5；
（2）①证明：过点B作EF⊥l1于E，交l4于F，作DM⊥l4于M，如图所示：则EF⊥l4，
∵四边形ABCD是正方形，
∴AB=BC，∠ABC=90°，
∴∠ABE+∠CBF=180°-90°=90°，
∵∠CBF+∠BCF=90°，
∴∠ABE=∠BCF，
在△ABE和△BCF中，
，
∴△ABE≌△BCF（AAS），
∴AE=BF，
同理△CDM≌△BCF（AAS），
∴△ABE≌△CDM（AAS），
∴BE=DM，
即h1=h2．
②解：由①得：AE=BF=h2+h2=h2+h1，
∵正方形ABCD的面积：S=AB2=AE2+BE2，
∴S=（h2+h1）2+h12=2h12+2h1h2+h3．
本题考查了正方形的性质、全等三角形的判定和性质、勾股定理等知识；熟练掌握正方形的性质，证明三角形全等是解题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、① 一组邻边相等的矩形是正方形
【解析】
根据正方形的判定定理添加一个条件使得矩形是菱形即可．
【详解】
解：∵四边形ABCD是矩形，AB=BC，
∴矩形ABCD为正方形（一组邻边相等的矩形是正方形）．
故答案为：①，一组邻边相等的矩形是正方形．
本题考查了正方形的判定定理，熟练掌握正方形的判定定理即可得到结论．
20、
【解析】
分析：根据方程的系数结合根的判别式,即可得出△=16-8m≥0,解之即可得出m的取值范围.
详解：∵关于x的方程有实数根,
∴△=(-4)²-4×2m=16-8m≥0,
解得:m≤2
故答案为:m≤2
点睛：本题考查了根的判别式,根的判别式大于0,方程有两个不相等的实数根;根的判别式等于0,方程有两个相等的实数根;根的判别式小于0,方程没有实数根.
21、（4，0）
【解析】
根据抛物线p＝ax2−10ax＋8（a＞0）经过点C、D和二次函数图象具有对称性，可以求得该抛物线顶点的横坐标和CD的长，然后根据菱形的性质和勾股定理可以求得AO的长，从而可以求得OB的长，进而写出点B的坐标．
【详解】
解：∵抛物线p＝ax2−10ax＋8＝a（x−5）2−25a＋8，
∴该抛物线的顶点的横坐标是x＝5，当x＝0时，y＝8，
∴点D的坐标为：（0，8），
∴OD＝8，
∵抛物线p＝ax2−10ax＋8（a＞0）经过点C、D，CD∥AB∥x轴，
∴CD＝5×2＝10，
∴AD＝10，
∵∠AOD＝90°，OD＝8，AD＝10，
∴AO＝，
∵AB＝10，
∴OB＝10−AO＝10−6＝4，
∴点B的坐标为（4，0），
故答案为：（4，0）
本题考查二次函数的性质、二次函数图象上点的坐标特征、菱形的性质，解答本题的关键是明确题意，利用二次函数的性质和数形结合的思想解答．
22、3或
【解析】
分两种情况：①当∠EFC=90°，先判断出点F在对角线AC上，利用勾股定理求出AC，设BE=x,表示出CE，根据翻折变换的性质得到AF=AB,EF=BE，再根据Rt△CEF利用勾股定理列式求解；②当∠CEF=90°，判断四边形ABEF是正方形，根据正方形的性质即可求解.
【详解】
分两种情况：①当∠EFC=90°，如图1，
∵∠AFE=∠B=90°，∠EFC=90°，
∴点A、F、C共线，
∵矩形ABCD的边AD=4，
∴BC=AD=4，
在Rt△ABC中，AC=
设BE=x，则CE=BC-BE=4-x，
由翻折的性质得AF=AB=3,EF=BE=x，∴CF=AC-AF=5-3=2
在Rt△CEF中，EF2+CF2=CE2，
即x2+22=(4-x)2，
解得x=；
②当∠CEF=90°，如图2
由翻折的性质可知∠AEB=∠AEF=45°，
∴四边形ABEF是正方形，
∴BE=AB=3，
故BE的长为3或
此题主要考查矩形的折叠问题，解题的关键是根据图形进行分类讨论.
23、-2
【解析】
将（1，－2）代入得，—2=1×k，解得k=－2
二、解答题（本大题共3个小题，共30分）
24、（1）；（2）且；（3）
【解析】
（1）根据一次函数平移的规律列方程组求解；
（2）将两点的坐标代入解析式得出方程组，根据方程组可得出a,b的等量关系式，然后根据b的取值范围，可求出a的取值范围，另外注意一次函数中二次项系数2a-3≠0的限制条件；
（3）先根据点P的坐标求出动点P所表示的直线表达式，再根据直线与平行得出结果.
【详解】
解：（1）依题意得
，
.
（2）过点和点
，
两式相减得；
解法一：，
当时，；
当时，.
，随的增大而增大
且，
.
，.
且.
解法二：
，
，解得.
，
∴.
且.
（3）设，
.
消去得，
动点的图象是直线.
不在上，
与平行，
，.
本题考查一次函数的图像与性质，以及一次函数平移的规律，掌握基本的性质是解题的关键.
25、这条小路的面积是140m1 .
【解析】
试题分析：根据勾股定理，可得BE的长，再根据路等宽，可得FD，根据矩形的面积减去两个三角形的面积，可得路的面积．
试题解析：路等宽，得BE=DF，
△ABE≌△CDF，
由勾股定理，得BE==80（m）
S△ABE=60×80÷1=1400（m1）
路的面积=矩形的面积﹣两个三角形的面积
=84×60﹣1400×1
=140（m1）．
答：这条小路的面积是140m1．
【点睛】本题考查了生活中的平移现象，先求出直角三角形的直角边的边长，再求出直角三角形的面积，用矩形的面积减去三角形的面积．
26、（1）详见解析；（2）；（3）
【解析】
（1）作△ABC的角平分线AE，作线段AE的垂直平分线交AB于D，交AC于F，连接DE、EF，四边形ADEF即为所求；
（2）由题意，当∠A=60°，AD=4时，△ADF，△EFD，△EMD都是等边三角形，边长为4，由此即可解决问题；
（3）利用三角形的中位线定理即可解决问题．
【详解】
（1）D，E，F的位置如图所示．
（2）由题意，当∠A=60°，AD=4时，△ADF，△EFD，△EMD都是等边三角形，边长为4，
∴S四边形AFEM=3××42=12；
（3）当AB=AC时，易知DE是△ABC的中位线，
∴DE=AC
∴=．
本题考查菱形的判定和性质，复杂作图，等边三角形的性质，三角形的中位线定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
题号
一
二
三
四
五
总分
得分