

2025届上海市廊下中学九上数学开学调研试题【含答案】
展开一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
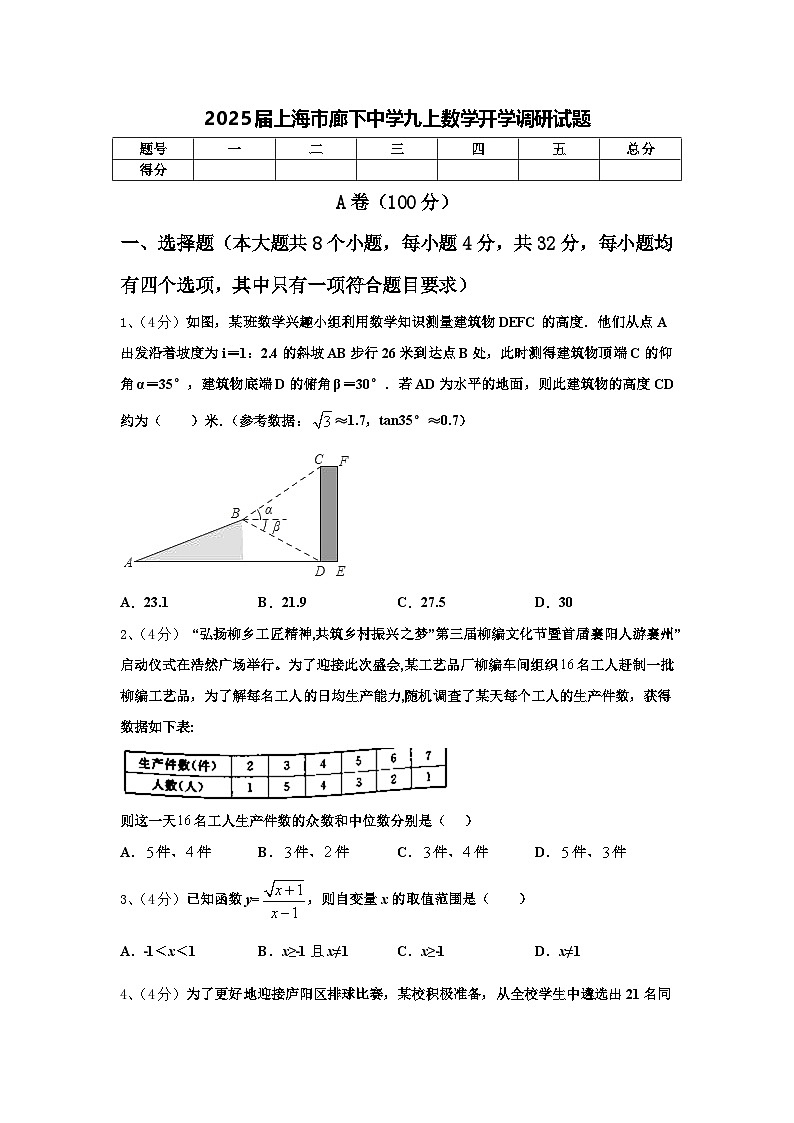
1、(4分)如图,某班数学兴趣小组利用数学知识测量建筑物DEFC的高度.他们从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,此时测得建筑物顶端C的仰角α=35°,建筑物底端D的俯角β=30°.若AD为水平的地面,则此建筑物的高度CD约为( )米.(参考数据:≈1.7,tan35°≈0.7)
A.23.1B.21.9C.27.5D.30
2、(4分) “弘扬柳乡工匠精神,共筑乡村振兴之梦”第三届柳编文化节暨首届“襄阳人游襄州”启动仪式在浩然广场举行。为了迎接此次盛会,某工艺品厂柳编车间组织名工人赶制一批柳编工艺品,为了解每名工人的日均生产能力,随机调查了某天每个工人的生产件数,获得数据如下表:
则这一天名工人生产件数的众数和中位数分别是( )
A.件、件B.件、件C.件、件D.件、件
3、(4分)已知函数y=,则自变量x的取值范围是( )
A.﹣1<x<1B.x≥﹣1且x≠1C.x≥﹣1D.x≠1
4、(4分)为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:
则该校排球队21名同学身高的众数和中位数分别是(单位:cm)( )
A.185,178B.178,175C.175,178D.175,175
5、(4分)如图,在菱形中,是菱形的高,若对角线、的长分别是6、8,则的长是
A.B.C.D.5
6、(4分)如图,已知正方形 ABCD 的边长为 10,E 在 BC 边上运动,取 DE 的中点 G,EG 绕点 E 顺时针旋转90°得 EF,问 CE 长为多少时,A、C、F 三点在一条直线上( )
A.B.C.D.
7、(4分)在一次中学生田径运动会上,男子跳高项目的成绩统计如下:
表中表示成绩的一组数据中,众数和中位数分别是
A.,B.,C.,D.,
8、(4分)已知一组数据:1,2,8,,7,它们的平均数是1.则这组数据的中位数是( )
A.7B.1C.5D.4
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是________.
10、(4分)(-4)2的算术平方根是________ 64的立方根是 _______
11、(4分)如图,在正方形的外侧,作等边三角形,则为__________.
12、(4分)已知x+y=﹣1,xy=3,则x2y+xy2=_____.
13、(4分)如图,在平行四边形ABCD中,连接AC,按以下步骤作图:分别以点A,C为圆心,以大于AC的长为半径画弧,两弧分别相交于点M,N,作直线MN交CD于点E,交AB于点F.若AB=5,BC=3,则△ADE的周长为__________.
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,已知平行四边形ABCD的周长是32 cm,,,,E,F是垂足,且
(1)求的度数;
(2)求BE,DF的长.
15、(8分)如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
16、(8分)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
17、(10分)如图,在直角坐标系中,,,是线段上靠近点的三等分点.
(1)若点是轴上的一动点,连接、,当的值最小时,求出点的坐标及的最小值;
(2)如图2,过点作,交于点,再将绕点作顺时针方向旋转,旋转角度为,记旋转中的三角形为,在旋转过程中,直线与直线的交点为,直线与直线交于点,当为等腰三角形时,请直接写出的值.
18、(10分)如图,直线与轴交于点,点是该直线上一点,满足.
(1)求点的坐标;
(2)若点是直线上另外一点,满足,且四边形是平行四边形,试画出符合要求的大致图形,并求出点的坐标.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)若关于的方程无解,则的值为________.
20、(4分)如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是_____
21、(4分)分解因式:___________.
22、(4分)如图,圆柱体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为_____.
23、(4分)如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=______.
二、解答题(本大题共3个小题,共30分)
24、(8分)因式分解:
(1)2x3﹣8x;
(2)(x+y)2﹣14(x+y)+49
25、(10分)如图,在△ABC中,∠ABC=90°,BD为AC边上的中线.
(1)按如下要求尺规作图,保留作图痕迹,标注相应的字母:过点C作直线CE,使CE⊥BC于点C,交BD的延长线于点E,连接AE;
(2)求证:四边形ABCE是矩形.
26、(12分)先化简,再求值:÷(2+),其中x=﹣1.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、B
【解析】
过点B作BN⊥AD,BM⊥DC垂足分别为N,M,设BN=x,则AN=2.4x,在Rt△ABN中,根据勾股定理求出x的值,从而得到BN和DM的值,然后分别在Rt△BDM和Rt△BCM中求出BM和CM的值,即可求出答案.
【详解】
如图所示:过点B作BN⊥AD,BM⊥DC垂足分别为N,M,
∵i=1:2.4,AB=26m,
∴设BN=x,则AN=2.4x,
∴AB==2.6x,
则2.6x=26,
解得:x=10,
故BN=DM=10m,
则tan30°= = = ,
解得:BM=10,
则tan35°== =0.7,
解得:CM≈11.9(m),
故DC=MC+DM=11.9+10=21.9(m).
故选B.
本题考查了解直角三角形的应用,如果没有直角三角形则作垂线构造直角三角形,然后利用直角三角形的边角关系来解决问题,有时还会用到勾股定理,相似三角形等知识才能解决问题.
2、C
【解析】
中位数是将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数,如果数据的个数是偶数就是中间两个数的平均数,众数是指一组数据中出现次数最多的数据.
【详解】
数据3出现的次数最多,所以众数为3件;
因为共16人,
所以中位数是第8和第9人的平均数,即中位数==4件,
故选:C.
本题考查众数和中位数,解题关键在于熟练掌握计算法则.
3、B
【解析】
根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,就可以求解.
【详解】
解:根据题意得:,
解得:x≥-1且x≠1.
故选B.
点睛:考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.
4、D
【解析】
找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据.
【详解】
解:因为175出现的次数最多,
所以众数是:175cm;
因为第十一个数是175,
所以中位数是:175cm.
故选:D.
本题为统计题,考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
5、B
【解析】
由菱形的性质可得AC⊥BD,BO=DO=4,CO=AO=3,由勾股定理可求CB=5,由菱形的面积公式可求AE的长.
【详解】
解:四边形是菱形
,,
故选:.
本题菱形的性质,熟练运用菱形的面积公式是本题的关键.
6、C
【解析】
过F作BC的垂线,交BC延长线于N点,连接AF.只要证明Rt△FNE∽Rt△ECD,利用相似比2:1解决问题.再证明△CNF是等腰直角三角形即可解决问题.
【详解】
过F作BC的垂线,交BC延长线于N点,连接AF.
∵∠DCE=∠ENF=90°,∠DEC+∠NEF=90°,∠NEF+∠EFN=90°,
∴∠DEC=∠EFN,
∴Rt△FNE∽Rt△ECD,
∵DE的中点G,EG绕E顺时针旋转90°得EF,
∴两三角形相似比为1:2,
∴可以得到CE=2NF,NE=CD=5.
∵AC平分正方形直角,
∴∠NFC=45°,
∴△CNF是等腰直角三角形,
∴CN=NF,
∴CE=NE=5=,
故选C.
本题考查正方形的性质和旋转的性质,解题的关键是掌握正方形的性质和旋转的性质.
7、B
【解析】
根据出现最多的数为众数解答;
按照从小到大的顺序排列,然后找出中间的一个数即为中位数.
【详解】
出现次数最多的数为1.55m,是众数;
21个数按照从小到大的顺序排列,中间一个是1.60m,所以中位数是1.60m.
故选B.
考查了众数,中位数的定义,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
8、A
【解析】
分析:首先根据平均数为1求出x的值,然后根据中位数的概念求解.
详解:由题意得:1+2+8+x+2=1×5,解得:x=2,这组数据按照从小到大的顺序排列为:2,1,2,2,8,则中位数为2.
故选A.
点睛:本题考查了中位数和平均数的知识,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数;平均数是指在一组数据中所有数据之和再除以数据的个数.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、三角形的中位线等于第三边的一半
【解析】
∵D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴DE=AB,
设DE=a,则AB=2a,
故答案是:三角形的中位线等于第三边的一半.
10、 4, 4
【解析】【分析】根据算术平方根和立方根的意义可求解.
【详解】因为42=16,43=64,
所以,(-4)2的算术平方根是4, 64的立方根是4.
故答案为:(1). 4, (2). 4
【点睛】本题考核知识点:算术平方根,立方根. 解题关键点:理解算术平方根,立方根的定义.
11、15
【解析】
分析:根据等边三角形的性质及正方形的性质可得到AB=AE,从而可求得∠BAE的度数,则可求∠AEB的度数.
详解:∵四边形是正方形,
∴,,
又∵是正三角形,
∴,,
∴,
∴为等腰三角形,,
∴.
故答案为:15.
点睛:主要考查了正方形和等边三角形的特殊性质,关键是根据等腰三角形的性质得到相等的角.
12、-1
【解析】
直接利用提取公因式法分解因式,进而把已知数据代入求出答案.
【详解】
解:∵x+y=﹣1,xy=1,∴x2y+xy2=xy(x+y)
=1×(﹣1)
=﹣1.
故答案为﹣1.
本题主要考查了提取公因式法分解因式,正确分解因式是解题的关键.
13、8
【解析】
解:由做法可知MN是AC的垂直平分线,
∴AE=CE.
∵四边形ABCD是平行四边形
∴CD=AB=5,AD=BC=3.
∴AD+DE+AE=AD+DE+CE=AD+CD=5+3=8,
∴△ADE的周长为8.
三、解答题(本大题共5个小题,共48分)
14、(1)∠C=60°;(2)BE=5cm,DF=3cm.
【解析】
(1)结合已知条件,由四边形的内角和为360°即可解答;(2)根据平行四边形的性质结合已知条件求得AB=10cm,BC=6cm.再根据30°角直角三角形的性质即可求解.
【详解】
(1)∵AE⊥BC,AF⊥CD,
∴∠AFD=∠AEB=90°,
∴∠EAF+∠C=360°﹣90°﹣90°=180°.
又∵∠EAF=2∠C,
∴∠C=60°.
(2)∵▱ABCD的周长是32cm,,
∴AB=10cm,BC=6cm.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠C=60°,
在Rt△ABE中,BE=AB,
∵AB=10 cm,
∴BE=5 cm,
同理DF=3 cm.
∴BE=5cm,DF=3cm.
本题考查了平行四边形的性质及30°角直角三角形的性质,熟练运用有关性质是解决问题的关键.
15、(1)BN=2﹣t;(2)当t=4﹣或t=3或t=2时,△DNE是等腰三角形;(3)当t=时,S取得最大值.
【解析】
(1)由等腰直角三角形的性质知AB=2,MN=AM=t,AN=﹣AM=﹣t,据此可得;
(2)先得出MN=DM=4﹣t,BP=PN=t﹣2,PE=4﹣t,由勾股定理得出NE=,再分DN=DE,DN=NE,DE=NE三种情况分别求解可得;
(3)分0≤t<2和2≤t≤4两种情况,其中0≤t<2重合部分为直角梯形,2≤t≤4时重合部分为等腰直角三角形,根据面积公式得出面积的函数解析式,再利用二次函数的性质求解可得.
【详解】
(1)如图1,
∵∠ACB=90°,AC=BC=2,
∴∠A=∠ABC=45°,AB=2,
∵AM=t,∠AMN=90°,
∴MN=AM=t,AN=AM=t,
则BN=AB﹣AN=
故答案为
(2)如图2,
∵AM=t,AC=BC=CD=2,∠BDC=∠DBE=45°,
∴DM=MN=AD﹣AM=4﹣t,
∴DN=DM=(4﹣t),
∵PM=BC=2,
∴PN=2﹣(4﹣t)=t﹣2,
∴BP=t﹣2,
∴PE=BE﹣BP=2﹣(t﹣2)=4﹣t,
则NE=,
∵DE=2,
∴①若DN=DE,则(4﹣t)=2,解得t=4﹣;
②若DN=NE,则(4﹣t)=,解得t=3;
③若DE=NE,则2=,解得t=2或t=4(点N与点E重合,舍去);
综上,当t=4﹣或t=3或t=2时,△DNE是等腰三角形.
(3)①当0≤t<2时,如图3,
由题意知AM=MN=t,
则CM=NQ=AC﹣AM=2﹣t,
∴DM=CM+CD=4﹣t,
∵∠ABC=∠CBD=45°,∠NQB=∠GQB=90°,
∴NQ=BQ=QG=2﹣t,
则NG=4﹣2t,
∴
当t=时,S取得最大值;
②当2≤t≤4时,如图4,
∵AM=t,AD=AC+CD=4,
∴DM=AD﹣AM=4﹣t,
∵∠DMN=90°,∠CDB=45°,
∴MN=DM=4﹣t,
∴S=(4﹣t)2=(t﹣4)2,
∵2≤t≤4,
∴当t=2时,S取得最大值2;
综上,当t=时,S取得最大值.
本题是四边形的综合问题,解题的关键是掌握正方形的性质和等腰直角三角形的判定与性质,等腰三角形的判定及二次函数性质的应用等知识点.
16、(1)这四名候选人面试成绩的中位数为89(分);(2)表中x的值为86;(3)以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
【解析】
(1)根据中位数的概念计算;
(2)根据题意列出方程,解方程即可;
(3)根据加权平均数的计算公式分别求出余三名候选人的综合成绩,比较即可.
【详解】
(1)这四名候选人面试成绩的中位数为:=89(分);
(2)由题意得,x×60%+90×40%=87.6
解得,x=86,
答:表中x的值为86;
(3)甲候选人的综合成绩为:90×60%+88×40%=89.2(分),
乙候选人的综合成绩为:84×60%+92×40%=87.2(分),
丁候选人的综合成绩为:88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
本题考查的是中位线、加权平均数,掌握中位数的概念、加权平均数的计算公式是解题的关键.
17、(1),;(2)α的值为45°,90°,135°,180°.
【解析】
(1)作HG⊥OB于H.由HG∥AO,求出OG,HG,即可得到点H的坐标,作点B关于y轴的对称点B′,连接B′H交y轴于点M,则B'(-2,0),此时MB+MH的值最小,最小值等于B'H的长;求得直线B′H的解析式为y= ,即可得到点M的坐标为.
(2)依据△OST为等腰三角形,分4种情况画出图形,即可得到旋转角的度数.
【详解】
解:(1)如图1,作HG⊥OB于H.
∵HG∥AO,
∴
∵OB=2,OA= ,
∴GB= ,HG= ,
∴OG=OB-GB= ,
∴H(,)
作点B关于y轴的对称点B′,连接B′H交y轴于点M,则B'(-2,0),
此时MB+MH的值最小,最小值等于B'H的长.
∵B'(-2,0),H(,)
B'H=
∴MB+MH的最小值为
设直线B'H的解析式为y=kx+b,则有
解得:
∴直线B′H的解析式为
当x=0时,y=
∴点M的坐标为:
(2)如图,当OT=OS时,α=75°-30°=45°;
如图,当OT=TS时,α=90°;
如图,当OT=OS时,α=90°+60°-15°=135°;
如图,当ST=OS时,α=180°;
综上所述,α的值为45°,90°,135°,180°.
本题考查几何变换综合题、平行线分线段成比例定理、轴对称最短问题、勾股定理、等腰三角形的判定和性质等知识,解题的关键是学会利用轴对称解决最短问题,学会用分类讨论的思想思考问题.
18、(1)点坐标为;(2)点.
【解析】
(1)先由直线y=-2x+10与x轴交于点A,求出点A坐标为(5,0),所以OA=5;再设点B坐标为(m,n),根据B是直线y=-2x+10上一点,及OB=OA,列出关于m,n的方程组,解方程组即可;
(2)由于四边形OBCD是平行四边形,根据平行四边形的对边平行且相等得出BC∥OD,BC=OD,再由AB=BC,得出AB=OD,根据一组对边平行且相等的四边形是平行四边形证明出四边形OABD是平行四边形,则BD∥OA且BD=OA=5,由平移的性质即可求出点D的坐标.
【详解】
(1)由已知,点坐标为,所以.
设点坐标为,
因为是直线上一点
∴
又, ∴
解得 或 (与点重合,舍去)
∴点坐标为.
(2)符合要求的大致图形如图所示。
∵平行四边形
∴且,
∵
∴,
∴四边形是平行四边形
∴且,
∴点.
本题考查了一次函数的综合题,涉及到一次函数图象上点的坐标的求法,二元二次方程组的解法,平行四边形的性质与判定,利用了方程思想及数形结合的思想,(2)中根据平行四边形的性质与判定证明出四边形OABD是平行四边形是解题的关键.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、
【解析】
分式方程去分母转化为整式方程,由分式方程无解得到x+1=0,求出x的值,代入整式方程求出m的值即可.
【详解】
去分母得:3x−2=2x+2+m,
由分式方程无解,得到x+1=0,即x=−1,
代入整式方程得:−5=−2+2+m,
解得:m=−5,
故答案为-5.
此题考查分式方程的解,解题关键在于掌握运算法则.
20、4
【解析】
根据平行四边形的判定定理首先推知四边形DBEC为平行四边形,然后由直角三角形斜边上的中线等于斜边的一半得到其邻边相等:CD=BD,得出四边形DBEC是菱形,由三角形中位线定理和勾股定理求得AB边的长度,然后根据菱形的性质和三角形的面积公式进行解答.
【详解】
∵CE∥DB,BE∥DC,
∴四边形DBEC为平行四边形.
又∵Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴CD=BD=AC,
∴平行四边形DBEC是菱形;
∵点D,F分别是AC,AB的中点,AD=3,DF=1,
∴DF是△ABC的中位线,AC=1AD=6,S△BCD=S△ABC,
∴BC=1DF=1.
又∵∠ABC=90°,
∴AB==.
∵平行四边形DBEC是菱形,
∴S四边形DBEC=1S△BCD=S△ABC=AB•BC=×4×1=4,
故答案为4.
考查了菱形的判定与性质,三角形中位线定理,直角三角形斜边上的中线以及勾股定理,熟练掌握相关的定理与性质即可解题.
21、ab(a+b)(a﹣b).
【解析】
分析:先提公因式ab,再把剩余部分用平方差公式分解即可.
详解:a3b﹣ab3,=ab(a2﹣b2),=ab(a+b)(a﹣b).
点睛:此题考查了综合提公因式法和公式法因式分解,分解因式掌握一提二用,即先提公因式,再利用平方差或完全平方公式进行分解.
22、10cm
【解析】
将圆柱沿过点A和点B的母线剪开,展开成平面,由圆柱路线可知小蚂蚁在水平方向爬行的路程等于个底面周长,从而求出解题中的AC,连接AB,根据两点之间线段最短可得小蚂蚁爬行的最短路程为此时AB的长,然后根据勾股定理即可求出结论.
【详解】
解:将圆柱沿过点A和点B的母线剪开,展开成平面,由圆柱路线可知小蚂蚁在水平方向爬行的路程等于个底面周长,如下图所示:AC=1.5×4=6cm,连接AB,根据两点之间线段最短,
∴小蚂蚁爬行的最短路程为此时AB的长
∵圆柱体的高为8cm,
∴BC=8cm
在Rt△ABC中,AB=cm
故答案为:10cm.
此题考查的是利用勾股定理求最短路径问题,将圆柱的侧面展开,根据两点之间线段最短即可找出最短路径,然后利用勾股定理求值是解决此题的关键.
23、4或1
【解析】
分别利用,当MN∥BC时,以及当∠ANM=∠B时,分别得出相似三角形,再利用相似三角形的性质得出答案.
【详解】
如图1,当MN∥BC时,
则△AMN∽△ABC,
故,
则,
解得:MN=4,
如图2所示:当∠ANM=∠B时,
又∵∠A=∠A,
∴△ANM∽△ABC,
∴,
即,
解得:MN=1,
故答案为:4或1.
此题主要考查了相似三角形判定,正确利用分类讨论得出是解题关键.
二、解答题(本大题共3个小题,共30分)
24、(1)1x(x+1)(x﹣1);(1)(x+y﹣7)1.
【解析】
(1)首先提取公因式1x,再利用平方差公式完全平方公式分解因式得出答案;
(1)直接利用完全平方公式分解因式得出答案.
【详解】
解:(1)原式=1x(x1﹣4)
=1x(x+1)(x﹣1);
(1)原式=(x+y﹣7)1.
此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.
25、 (1)见解析;(2)见解析.
【解析】
(1)根据题意作图即可;
(2)先根据BD为AC边上的中线,AD=DC,再证明△ABD≌△CED(AAS)得AB=EC,已知∠ABC=90°即可得四边形ABCE是矩形.
【详解】
(1)解:如图所示:E点即为所求;
(2)证明:∵CE⊥BC,
∴∠BCE=90°,
∵∠ABC=90°,
∴∠BCE+∠ABC=180°,
∴AB∥CE,
∴∠ABE=∠CEB,∠BAC=∠ECA,
∵BD为AC边上的中线,
∴AD=DC,
在△ABD和△CED中
,
∴△ABD≌△CED(AAS),
∴AB=EC,
∴四边形ABCE是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCE是矩形.
本题考查了全等三角形的判定与性质与矩形的性质,解题的关键是熟练的掌握全等三角形的判定与性质与矩形的性质.
26、当x=﹣1时,原式==.
【解析】试题分析:原式=÷=÷==,当x=﹣1时,原式==.
考点:分式的化简求值.
题号
一
二
三
四
五
总分
得分
身高(cm)
170
172
175
178
180
182
185
人数(个)
2
4
5
2
4
3
1
成绩
人数
2
8
6
4
1
修造人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
2025届海南省农垦中学数学九上开学调研试题【含答案】: 这是一份2025届海南省农垦中学数学九上开学调研试题【含答案】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2025届广东省中学山市板芙镇数学九上开学调研试题【含答案】: 这是一份2025届广东省中学山市板芙镇数学九上开学调研试题【含答案】,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024年上海市普陀区名校九上数学开学调研试题【含答案】: 这是一份2024年上海市普陀区名校九上数学开学调研试题【含答案】,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












