高一预习-5.4 三角函数的图像与性质（学生版）-初升高数学暑假衔接（人教版）

这是一份高一预习-5.4 三角函数的图像与性质（学生版）-初升高数学暑假衔接（人教版），共11页。学案主要包含了知识梳理，基础自测，例题详解，课堂巩固，课时作业等内容，欢迎下载使用。

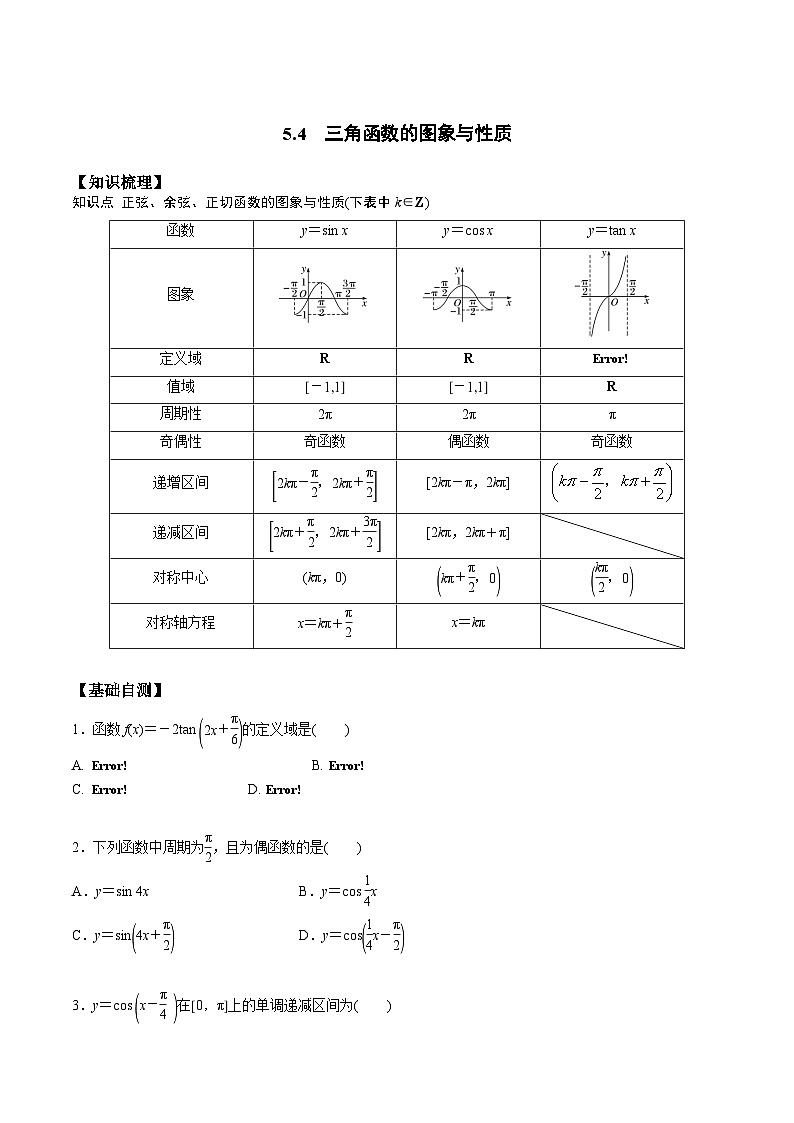
知识点 正弦、余弦、正切函数的图象与性质(下表中k∈Z)
【基础自测】
1．函数f(x)＝－2taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的定义域是( )
A. eq \b\lc\{\rc\}(\a\vs4\al\c1(x∈R\b\lc\|\rc\ (\a\vs4\al\c1(x≠\f(π,6))))) B. eq \b\lc\{\rc\}(\a\vs4\al\c1(x∈R\b\lc\|\rc\ (\a\vs4\al\c1(x≠－\f(π,12)))))
C. eq \b\lc\{\rc\}(\a\vs4\al\c1(x∈R\b\lc\|\rc\ (\a\vs4\al\c1(x≠kπ＋\f(π,6)k∈Z)))) D. eq \b\lc\{\rc\}(\a\vs4\al\c1(x∈R\b\lc\|\rc\ (\a\vs4\al\c1(x≠\f(kπ,2)＋\f(π,6)k∈Z))))
2．下列函数中周期为eq \f(π,2)，且为偶函数的是( )
A．y＝sin 4x B．y＝cs eq \f(1,4)x
C．y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(π,2))) D．y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4)x－\f(π,2)))
3．y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))在[0，π]上的单调递减区间为( )
A. eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)，\f(3π,4))) B. eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,4))) C. eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3π,4)，π)) D. eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)，π))
4．函数y＝3cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x－\f(π,4)))在x＝________时，y取最大值．
5．函数y＝－tan2x＋4tan x＋1，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,4)，\f(π,4)))的值域为________．
【例题详解】
一、三角函数的定义域
例1 (1)函数y＝eq \r(sin x－cs x)的定义域为________．
(2)函数y＝taneq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))的定义域是( )
A. eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠\f(π,4))))) B. eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠－\f(π,4)))))
C. eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠kπ＋\f(π,4)，k∈Z)))) D. eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠kπ＋\f(3π,4)，k∈Z))))
跟踪训练1 (1)函数f(x)＝ln(cs x)的定义域为( )
eq \b\lc\(\rc\)(\a\vs4\al\c1(kπ－\f(π,2)，kπ＋\f(π,2)))，k∈Z B．(kπ，kπ＋π)，k∈Z
C. eq \b\lc\(\rc\)(\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))，k∈Z D．(2kπ，2kπ＋π)，k∈Z
(2)函数的定义域为__________．
二、三角函数的值域
例2 (1)函数，的值域是（ ）
A．B．C．D．
(2)函数y=tan（+），x∈（0，]的值域是______．
(3)函数y＝4cs2x＋4cs x－2的值域是（ ）
A． B． C． D．
跟踪训练2 (1)函数的值域为（ ）
A．[0，1]B．C．D．
(2)函数，的值域为____________．
题型三、三角函数的周期性
例3 (1)下列函数中，是周期函数的为( )
A．y＝sin|x| B．y＝cs|x|
C．y＝tan|x| D．y＝(x－1)0
(2)在函数①，② ，③,④中，最小正周期为的所有函数为
A．①②③B．①③④C．②④D．①③
跟踪训练3 下列函数中周期为且为偶函数的是（ ）
A．B．
C．D．
题型四、三角函数的对称性
例4 (1)若函数的最小正周期为，则它的一条对称轴是（ ）
A．B．
C．D．
(2)函数的图象的一个对称中心可以是（ ）
A． B． C． D．
(3)已知函数的图像关于直线对称，则可能取值是（ ）.
A．B．C．D．
跟踪训练4 (1)函数的一个对称中心是（ ）
A．B．C．D．
(2)如果函数y=3cs(2x+φ)的图象关于点对称，那么|φ|的最小值为（ ）
A． B． C． D．
题型五、三角函数的单调性
例5 (1)函数的单调递增区间是（ ）
A．，
B．，
C．，
D．，
(2)已知，，，则，，的大小关系为（ ）
A．B．C．D．
(3)函数的单调递减区间为___________.
跟踪训练5 (1)函数的单调增区间是__________．
(2)下列各式中正确的是（ ）
A．B．
C．D．
【课堂巩固】
1．函数，的值域是（ ）
A．B．C．D．
2．设则（ ）
A．B．C．D．
3．下列关系中，正确的是（ ）
A．B．
C．D．
4．已知函数，，其函数图象的一个对称中心是，则该函数的一个单调递减区间是（ ）
A．B．C．D．
5．已知函数，下面结论错误的是（ ）
A．函数的最小正周期为B．函数在区间上是增函数
C．函数的图像关于直线对称D．函数是奇函数
6．已知，函数在上单调递减，则的取值范围是（ ）
A．B．C．D．
7．已知函数，则下列说法正确的是（ ）
A．的最小正周期是
B．的值域是
C．直线是函数图像的一条对称轴
D．的递减区间是，
8．函数的单调递增区间为__________．
9．函数的定义域为_____________ ．
10．已知，则实数的大小关系为__________.
11．关于下列命题：
①若是第一象限角，且，则；
②函数是偶函数；
③函数的一个对称中心是；
④函数在上是增函数，
所有正确命题的序号是_____．
12．已知函数.
(1)求的定义域、值域；
(2)探究的周期性、奇偶性、单调性及其图象的对称性.
【课时作业】
1．函数的最大值为（ ）
A．1B．0C．2D．
2．已知，，，则下列关系中正确的是
A．B．C．D．
3．对于函数，有以下四种说法：
①函数的最小值是
②图象的对称轴是直线
③图象的对称中心为
④函数在区间上单调递增．
其中正确的说法的个数是（ ）
A．1B．2C．3D．4
4．函数的单调递增区间是（ ）
A．，k∈ZB．，k∈Z
C．，k∈ZD．，k∈Z
5．已知函数的一个零点是，是的图象的一条对称轴，则取最小值时，的单调递增区间是（ ）
A．，B．，
C．，D．，
6．已知函数图象的相邻两条对称轴间的距离为，且，则不等式的解集为（ ）
A． B．
C． D．
7．设,,,c，则下列关系式正确的是 （______）
A．B．.C．D．
8．函数有（ ）个不同的零点
A．3B．4C．5D．6
9．（多选）若函数，则下列命题正确的是（ ）
A．函数的图象与的图象重合
B．
C．
D．存在唯一的，使得
10．函数的单调递减区间为________.
11．已知函数，是偶函数，则______.
12．已知，函数在上单调递减，则的取值范围是_______．
13．若函数的图像在上恰好有一个点的纵坐标为，则实数的值可以是__________（写出一个满足题意的值即可）．
14．给出下列四个命题：
函数的一条对称轴是；
函数的图象关于点对称；
若，则，其中；
④函数的最小值为.
以上四个命题中错误的个数为____________个.
15．已知函数的最小正周期为.
（1）求的单调增区间和对称轴；
（2）若，求的最大值和最小值.
16．已知函数．
(1)令，判断函数的奇偶性；
(2)求在区间上的最值．
17．若x∈[－， ]，求函数y＝＋2tanx＋1的最值及相应的x的值．
18．求下列函数的值域：
（1）；
（2）．
函数
y＝sin x
y＝cs x
y＝tan x
图象
定义域
R
R
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠kπ＋\f(π,2)))))
值域
[－1,1]
[－1,1]
R
周期性
2π
2π
π
奇偶性
奇函数
偶函数
奇函数
递增区间
eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))
[2kπ－π，2kπ]
递减区间
eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ＋\f(π,2)，2kπ＋\f(3π,2)))
[2kπ，2kπ＋π]
对称中心
(kπ，0)
eq \b\lc\(\rc\)(\a\vs4\al\c1(kπ＋\f(π,2)，0))
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)，0))
对称轴方程
x＝kπ＋eq \f(π,2)
x＝kπ