广东省广州市培英中学2024-2025学年高二上学期10月学情调查数学试题(无答案)

这是一份广东省广州市培英中学2024-2025学年高二上学期10月学情调查数学试题(无答案)，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
本试卷共4页，19小题，满分150分。考试用时120分钟。
一、选择题：本大题共8小题，每小题5分，共40分。在每小题列出的四个选项中，只有一项符合题目要求。
1.故宫文创店推出了紫禁城系列名为“春”、“夏”、“秋”、“冬”的四款书签，并随机选择一款作为纪念品赠送给游客甲，则游客甲得到“春”或“冬”款书签的概率为（ ）
A.B.C.D.
2.下列命题正确的是（ ）
A.若，，则
B.若，，则
C.若，，则
D.若，，则
3.从1，2，3，4，5中随机选取2个不同的数，则所选的2个数中恰好有1个数是质数的概率为（ ）
A.B.C.D.
4.如果，，三点在同一条直线上，那么（ ）
A.，B.，
C.，D.，
5.如图，已知电路中4个开关闭合的概率都是，且是相互独立的，则灯亮的概率为（ ）
A.B.C.D.
6.利用简单随机抽样的方法抽查某工厂的100件产品，其中一等品有20件，合格品有70件，其余为不合格品，现在这个工厂随机抽查一件产品，设事件A为“是一等品”，B为“是合格品”，C为“是不合格品”，则下列结果错误的是（ ）
A.B.
C.D.
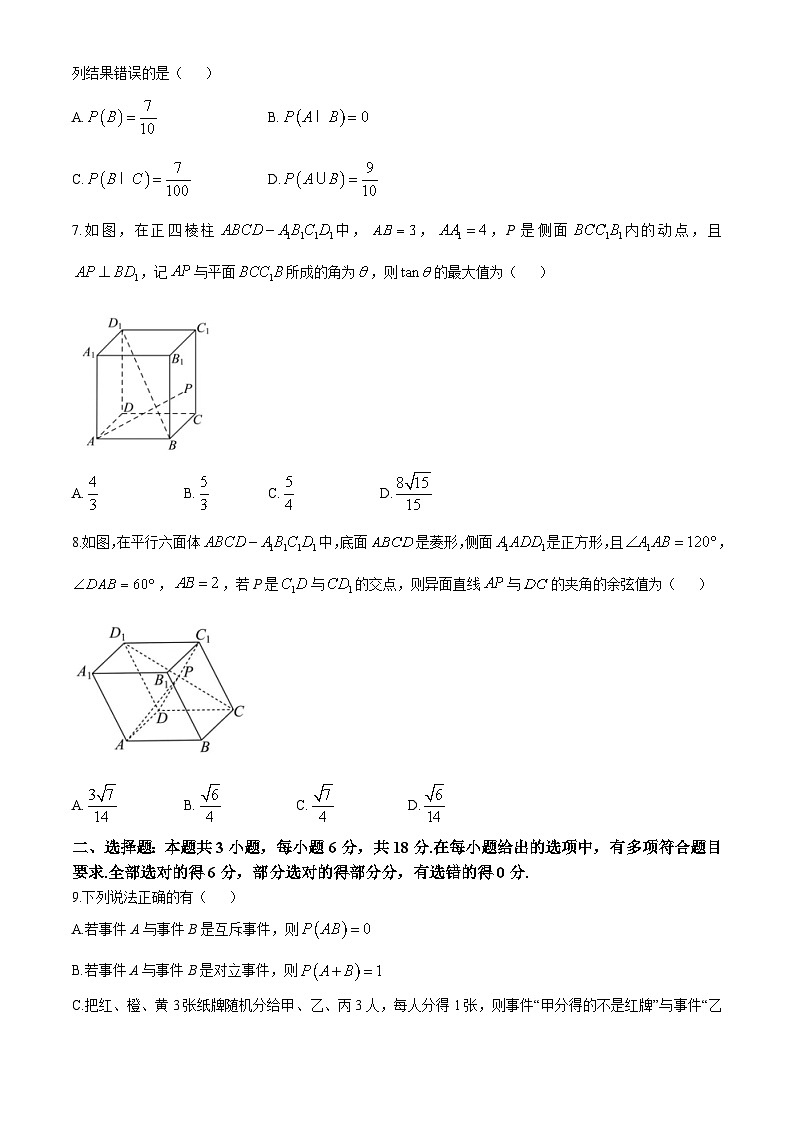
7.如图，在正四棱柱中，，，P是侧面内的动点，且，记与平面所成的角为，则的最大值为（ ）
A.B.C.D.
8.如图，在平行六面体中，底面是菱形，侧面是正方形，且，，，若P是与的交点，则异面直线与的夹角的余弦值为（ ）
A.B.C.D.
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9.下列说法正确的有（ ）
A.若事件A与事件B是互斥事件，则
B.若事件A与事件B是对立事件，则
C.把红、橙、黄3张纸牌随机分给甲、乙、丙3人，每人分得1张，则事件“甲分得的不是红牌”与事件“乙分得的不是红牌”是互斥事件
D.某人打靶时连续射击三次，则事件“至少有两次中靶”与事件“至多有一次中靶”是对立事件
10.若是空间的一个基底，则下列向量中可以和，构成空间一个基底的是（ ）
A.B.C.D.
11.在棱长为2的正方体中，E，F，G分别为棱，，的中点，则（ ）
A.B.是平面的一个法向量
C.点C到平面的距离为D.直线到直线的距离是
三、填空题：本大题共3小题，每小题5分，共15分.
12.在空间直角坐标系中，点（2，-3，5）关于平面的对称点的坐标为______.
13.三个空间向量，，不共面，且存在实数x，y，z，使.则______.
14.甲、乙两队进行篮球决赛，采取七场四胜制（当一队赢得四场胜利时，该队获胜，决赛结束）.甲队的主客场安排依次为“主主客客主客主”，设甲队主场取胜的概率为0.7，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4：1获胜的概率为______.
四、解答题：本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤。
15.（13分）如图，在平行六面体中，，.
（1）求体对角线的长度；
（2）求证：四边形为正方形.
16.（15分）某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为.
（1）求频率分布直方图中的值；
（2）估计该企业的职工对该部门评分不低于80的概率；
（3）从评分在的受访职工中，随机抽取2人，求此2人评分都在的概率.
17.（15分）如图，在四棱锥中，面，，，，点E是线段中点.
（1）求证：平面；
（2）若，求二面角的余弦值
18.（17分）甲、乙、丙三人玩“剪刀、石头、布”游戏（剪刀赢布，布赢石头，石头赢剪刀），规定每局中：①三人出现同一种手势，每人各得1分；②三人出现两种手势，赢者得2分，输者负1分；③三人出现三种手势均得0分.当有人累计得3分及以上时，游戏结束，得分最高者获胜，已知三人之间及每局游戏互不受影响.
（1）求甲在一局中得2分的概率；
（2）求游戏经过两局后甲恰得3分且为唯一获胜者的概率；
（3）求游戏经过两局就结束的概率.
19.（17分）我们把和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线.如图，在菱形中，，将沿翻折，使点A到点P处.E，F，G分别为，，的中点，且是与的公垂线.
（1）证明：三棱锥为正四面体；
（2）若点M，N分别在，上，且为与的公垂线.
①求的值；
②记四面体的内切球半径为，证明：.