安徽省安庆宿松县联考2025届九上数学开学联考模拟试题【含答案】

这是一份安徽省安庆宿松县联考2025届九上数学开学联考模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知一组数据1，l，，7，3，5，3，1的众数是1，则这组数据的中位数是( )．
A．1B．1．5C．3D．5
2、（4分）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．等边三角形B．等腰梯形C．正方形D．平行四边形
3、（4分）如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为（ ）
A．4B．3C．D．2
4、（4分）函数y1=x+1与y2=ax+b（a≠0）的图象如图所示，这两个函数图象的交点在y轴上，那么使y1＞y2的x的取值范围是（ ）
A．x＞0B．x＞1C．x＞-1D．-1＜x＜2
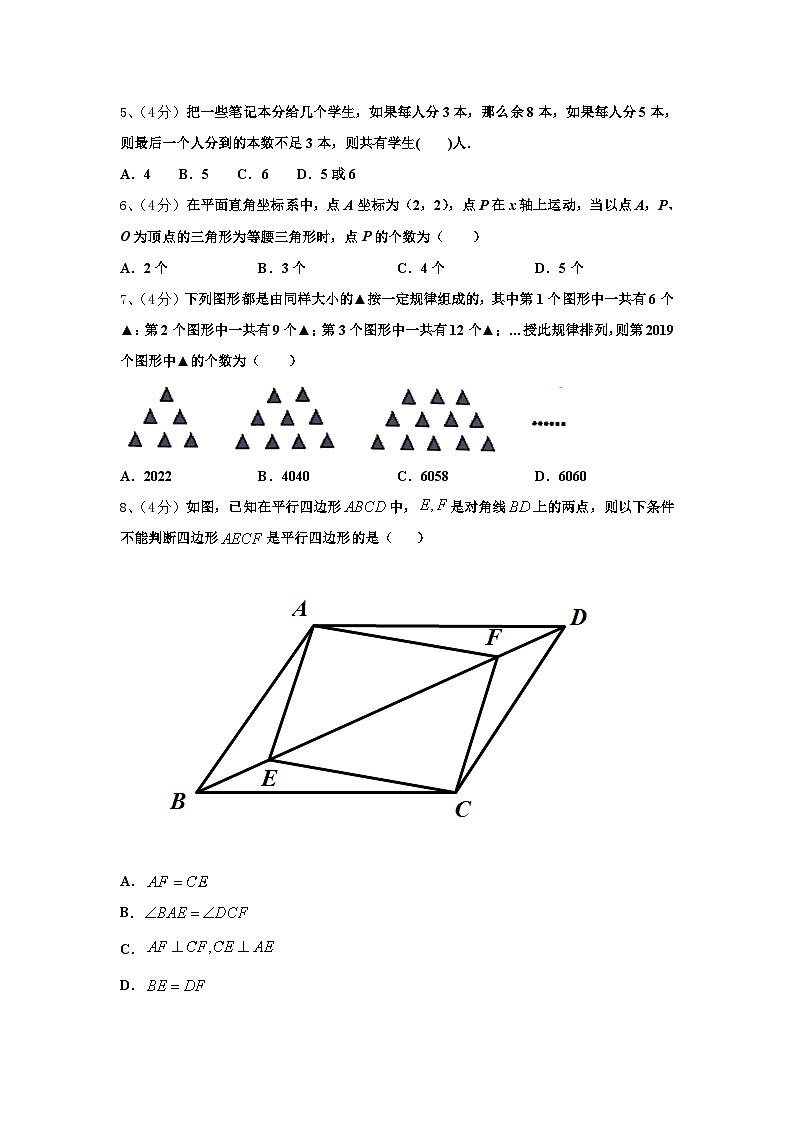
5、（4分）把一些笔记本分给几个学生，如果每人分3本，那么余8本，如果每人分5本，则最后一个人分到的本数不足3本，则共有学生( )人．
A．4 B．5 C．6 D．5或6
6、（4分）在平面直角坐标系中，点A坐标为（2，2），点P在x轴上运动，当以点A，P、O为顶点的三角形为等腰三角形时，点P的个数为（ ）
A．2个B．3个C．4个D．5个
7、（4分）下列图形都是由同样大小的▲按一定规律组成的，其中第1个图形中一共有6个▲：第2个图形中一共有9个▲；第3个图形中一共有12个▲；…授此规律排列，则第2019个图形中▲的个数为（ ）
A．2022B．4040C．6058D．6060
8、（4分）如图，已知在平行四边形中，是对角线上的两点，则以下条件不能判断四边形是平行四边形的是（ ）
A．
B．
C．
D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，中，,点在上，,将线段沿方向平移得到线段，点分别落在边上，则的周长是 cm.
10、（4分）一组数据：3，5，9，12，6的极差是_________．
11、（4分）如图，在平行四边形ABCD中，对角线AC与BD相交于点O，若再添加一个条件，就可得平行四边形ABCD是矩形，则你添加的条件是_____．
12、（4分）如图，矩形ABCD 的对角线AC，BD的交点为O，点E为BC边的中点，，如果OE=2，那么对角线BD的长为______．
13、（4分）当x___________时，是二次根式．
三、解答题（本大题共5个小题，共48分）
14、（12分）作一直线，将下图分成面积相等的两部分（保留作图痕迹）．
15、（8分）某中学开展“我的中国梦”演讲比赛活动，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如下图所示．
（1）根据如图，分别求出两班复赛的平均成绩和方差；
（2）根据（1）的计算结果，分析哪个班级5名选手的复赛成绩波动小？
16、（8分）如图，正方形ABCD的对角线AC和BD相交于点O，正方形A1B1C1O的边OA1交AB于点E，OC1交BC于点F．
（1）求证：（BE+BF）2=2OB2；
（2）如果正方形ABCD的边长为a，那么正方形A1B1C1O绕O点转动的过程中，与正方形ABCD重叠部分的面积始终等于 （用含a的代数式表示）
17、（10分）我们可用表示以为自变量的函数，如一次函数，可表示为，且，，定义:若存在实数，使成立，则称为的不动点，例如：，令，得，那么的不动点是1.
（1）已知函数，求的不动点.
（2）函数（是常数）的图象上存在不动点吗？若存在，请求出不动点；若不存在，请说明理由；
（3）已知函数（），当时，若一次函数与二次函数的交点为，即两点的横坐标是函数的不动点，且两点关于直线对称，求的取值范围.
18、（10分）如图①，在正方形ABCD中，，点E，F分别在BC、CD上，，试探究面积的最小值。
下面是小丽的探究过程：
(1)延长EB至G，使，连接AG，可以证明．请完成她的证明；
(2)设，,
①结合（1）中结论，通过计算得到与x的部分对应值。请求出表格中a的值：（写出解答过程）
②利用上表和（1）中的结论通过描点、连线可以分别画出函数、的图像、请在图②中完善她的画图；
③根据以上探究，估计面积的最小值约为（结果估计到1．1）。

图① 图②
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）要使代数式有意义，则的取值范围是________．
20、（4分）如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值是________ ．

21、（4分）菱形ABCD的周长为24，∠ABC=60°，以AB为腰在菱形外作底角为45°的等腰△ABE，连结AC，CE，则△ACE的面积为___________.
22、（4分）如图，将长8cm，宽4cm的矩形ABCD纸片折叠，使点A与C重合，则折痕EF的长为_________cm．
23、（4分）若数据10，9，a，12，9的平均数是10，则这组数据的方差是_____
二、解答题（本大题共3个小题，共30分）
24、（8分）嘉淇同学要证明命“两相对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图，在四边形ABCD中，
BC＝AD，
AB＝____．
求证：四边形ABCD是____四过形．
（1）在方框中填空，以补全已知和求证；
（2）按嘉淇的想法写出证明：
证明：
（3）用文宇叙述所证命题的逆命题为____________________．
25、（10分）下图反映的过程是小明从家去菜地浇水，又去玉米地锄草，然后回家．其中x表示时间，y表示小明离他家的距离．根据图象回答下列问题：
①菜地离小明家多远？小明走到菜地用了多少时间？
②小明给菜地浇水用了多少时间？
③玉米地离菜地、小明家多远？小明从玉米地走回家平均速度是多少？
26、（12分）如图，一次函数的图象与反比例函数（）的图象交于A（-3，2），B（n，4）两点．
（1）求一次函数与反比例函数的解析式；
（2）点C（-1，0）是轴上一点，求△ABC的面积．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
数据1，1，x，7，3，2，3，1的众数是1，说明1出现的次数最多，所以当x=1时，1出现3次，次数最多，是众数；再把这组数据从小到大排列：1，1，1，1，3，3，2，7，处于中间位置的数是1和3，所以中位数是：（1+3）÷1=1.2．
故选B.
2、C
【解析】
根据轴对称图形和中心对称图形的概念，即可求解．
【详解】
解：A、B都只是轴对称图形；
C、既是轴对称图形，又是中心对称图形；
D、只是中心对称图形．
故选：C．
掌握好中心对称图形与轴对称图形的概念是解题的关键．
3、B
【解析】
根据平行四边形性质得出AB=DC，AD∥BC，推出∠DEC=∠BCE，求出∠DEC=∠DCE，推出DE=DC=AB，得出AD=2DE即可．
【详解】
解：∵四边形ABCD是平行四边形，
∴AB=DC，AD∥BC，
∴∠DEC=∠BCE，
∵CE平分∠DCB，
∴∠DCE=∠BCE，
∴∠DEC=∠DCE，
∴DE=DC=AB，
∵AD=2AB=2CD，CD=DE，
∴AD=2DE，
∴AE=DE=3，
∴DC=AB=DE=3，
故选B．
本题考查了平行四边形性质，平行线性质，角平分线定义，等腰三角形的性质和判定的应用，关键是求出DE=AE=DC．
4、A
【解析】
当x＞0时，函数y1=x+1的图象在函数y2=ax+b（a≠0）的图象上方，据此可得使y1＞y2的x的取值范围是x＞0
【详解】
由图可得，当x＞0时，函数y1=x+1的图象在函数y2=ax+b（a≠0）的图象的上方，
∴使y1＞y2的x的取值范围是x＞0，
故选：A．
本题主要考查了一次函数与一元一次不等式的关系，解答此题的关键是利用数形结合的思想方法求解。
5、C
【解析】
根据每人分3本，那么余8本，如果前面的每个学生分1本，那么最后一人就分不到3本，得出3x+8≥1（x-1），且1（x-1）+3＞3x+8，分别求出即可．
【详解】
假设共有学生x人，根据题意得出：
1（x-1）+3＞3x+8≥1（x-1），
解得：1＜x≤6.1．
故选：C．
本题考查了不等式组的应用，解题关键是根据题意找出不等关系得出不等式组．
6、C
【解析】
先分别以点O、点A为圆心画圆，圆与x轴的交点就是满足条件的点P，再作OA的垂直平分线，与x轴的交点也是满足条件的点P，由此即可求得答案.
【详解】
如图，当OA=OP时，可得P1、P2满足条件，
当OA=AP时，可得P3满足条件，
当AP=OP时，可得P4满足条件，
故选C.
本题考查了等腰三角形的判定和坐标与图形的性质，正确的分类并画出图形是解题的关键.
7、D
【解析】
仔细观察图形，找到图形中圆形个数的通项公式，然后代入n=100求解即可．
【详解】
解：观察图形得：
第1个图形有3+3×1=6个三角形，
第2个图形有3+3×2=9个三角形，
第3个图形有3+3×3=12个三角形，
…
第n个图形有3+3n=3（n+1）个三角形，
当n=2019时，3×（2019+1）=6060，
故选D．
本题考查了图形的变化类问题，解题的关键是仔细的读题并找到图形变化的规律，难度不大．
8、A
【解析】
连接AC与BD相交于O，根据平行四边形的对角线互相平分可得OA=OC，OB=OD，再根据对角线互相平分的四边形是平行四边形，只要证明得到OE=OF即可，然后根据各选项的条件分析判断即可得解．
【详解】
解：如图，连接AC与BD相交于O，
在▱ABCD中，OA=OC，OB=OD，
要使四边形AECF为平行四边形，只需证明得到OE=OF即可；
A、AF=EF无法证明得到OE=OF，故本选项正确．
B、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等，从而得到DF=BE，则OB-BE=OD-DF，即OE=OF，故本选项错误；
C、若AF⊥CF，CE⊥AE，由直角三角形的性质可得OE=AC=OF，故本选项错误；
D、若BE=DF，则OB-BE=OD-DF，即OE=OF，故本选项错误；
故选：A．
本题考查了平行四边形的判定与性质，熟练掌握平行四边形的判定方法是解题的关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、13.
【解析】
试题分析：∵CD沿CB平移7cm至EF
考点：平移的性质；等腰三角形的性质.
10、1
【解析】
根据极差的定义求解．
【详解】
解：数据：3，5，1，12，6，所以极差=12-3=1．
故答案为：1．
本题考查了极差的定义，它反映了一组数据变化范围的大小，求极差的方法是用一组数据中的最大值减去最小值．
11、AC=BD或∠ABC=90°．
【解析】
矩形是特殊的平行四边形，矩形有而平行四边形不具有的性质是：矩形的对角线相等，矩形的四个内角是直角；可针对这些特点来添加条件．
【详解】
：若使ABCD变为矩形，可添加的条件是：
AC=BD；（对角线相等的平行四边形是矩形）
∠ABC=90°等．（有一个角是直角的平行四边形是矩形）
故答案为AC=BD或∠ABC=90°．
此题主要考查的是平行四边形的性质及矩形的判定方法，熟练掌握矩形和平行四边形的联系和区别是解答此题的关键．
12、1
【解析】
由30°角直角三角形的性质求得，然后根据矩形的两条对角线相等且平分来求的长度．
【详解】
解：在矩形中，对角线，的交点为，
，，．
又∵点为边的中点，
，
，，
，
，
．
故答案为：1．
本题主要考查对矩形的性质，三角形的中位线定理，能根据矩形的性质和30°角所对的直角边等于斜边的一半求出的长是解此题的关键．题型较好，难度适中．
13、≤；
【解析】
因为二次根式满足的条件是:含二次根号,被开方数大于或等于0,利用二次根式满足的条件进行求解.
【详解】
因为是二次根式,
所以,
所以,
故答案为.
本题主要考查二次根式的定义,解决本题的关键是要熟练掌握二次根式的定义.
三、解答题（本大题共5个小题，共48分）
14、见解析
【解析】解：将此图形分成两个矩形，分别作出两个矩形的对角线的交点，，
则，分别为两矩形的对称中心，过点，的直线就是所求的直线，如图所示.
E
F
15、（1）九(1)班成绩的平均数为85，方差为70；九(2)班成绩的平均数为85，方差为160；（2）九(1)班方差小，成绩波动小
【解析】
（1）从直方图中得到各个选手的得分，由平均数和方差的公式计算；
（2）由方差的意义分析．
【详解】
(1)九(1)班的选手的得分分别为85，75，80，85，100，
∴九(1)班成绩的平均数=(85+75+80+85+100)÷5=85，
九(1)班的方差 =[(85−85) +(75−85) +(80−85) +(85−85) +(100−85) ]÷5=70；
九(2)班的选手的得分分别为70，100，100，75，80，
九(2)班成绩的平均数=(70+100+100+75+80)÷5=85，
九(2)班的方差 =[(70−85) +(100−85) +(100−85) +(75−85) +(80−85) ]÷5=160；
(2)平均数一样的情况下,九(1)班方差小，成绩波动小。
此题考查用样本估计总体，加权平均数，方差，条形统计图，解题关键在于看懂图中数据
16、（1）证明见解析；（1）．
【解析】
（1）由题意得OA=OB，∠OAB=∠OBC=45°又因为∠AOE+∠EOB=90°，∠BOF+∠EOB=90°可得∠AOE=∠BOF，根据ASA可证△AOE≌△BOF，可得AE=BF，可得BE+BF=AB，由勾股定理可得结论；
（1）由全等三角形的性质可得S△AOE=S△BOF，可得重叠部分的面积为正方形面积的，即可求解．
【详解】
解：（1）在正方形ABCD中，AO=BO，∠AOB=90°，∠OAB=∠OBC=45°．
∵∠AOE+∠EOB=90°，∠BOF+∠EOB=90°，∴∠AOE=∠BOF．
在△AOE和△BOF中
，
∴△AOE≌△BOF（ASA），
∴AE=BF，
∴BE+EF=BE+AE=AB
在Rt△AOB中，AB1=OA1+OB1，且OA=OB，
∴（BE+BF）1=1OB1，
（1）∵△AOE≌△BOF，
∴S△AOE=S△BOF，
∴重叠部分的面积=S△AOB=S正方形ABCD=a1．
故答案为：a1．
本题考查了正方形的性质和全等三角形的判定和性质，掌握全等三角形的判定是解题的关键.
17、（1的不动点为0和2；（2）①时，有唯一的不动点②时，有无数个不动点③时，没有不动点；（3）的取值范围是
【解析】
（1）根据不动点的性质即可列方程求解；
（2）令，得：，根据m,n的取值进行讨论即可求解；
（3）令，则，根据一元二次方程根与系数求出A,B的中点C的坐标，再根据点在直线上，得到，得到b关于a的二次函数，再根据二次函数的性质即可求解.
【详解】
解：（1）令，则，，.
所以,的不动点为0和2.
（2）令，得：.
①若，即时，有唯一的不动点;
②若，，即时，有无数个不动点;
③若，即时，没有不动点0.
（3）令，则.
设，，则，.
的中点坐标为
，.
所以,
点在直线上，
所以,.
.
当时，.
此时，恒大于0
所以,的取值范围是:.
此题主要考查二次函数的应用，解题的关键是根据题意理解不动点的定义与性质.
18、（1）见解析；（2）①，②见解析；③41.4或41.5.
【解析】
（1）AB=AD，BG=DF，则AG=AF，∠DAF+∠BAE=91°-∠EAF=45°=∠EAF，AF=AG，AE=AE，则△AFE≌△AGE（SAS），即可求解；
（2）①∵CE=BC-6=4，设DF=a，CF=11-a，EF=DF+BE=6+a，由勾股定理即可求解；②由①得：y2=y1+x，描点画图即可；
（3）利用分割法即可得出．
【详解】
（1）证明：如图①，延长EB至G，使，连接AG.
四边形ABCD是正方形，
，，
，
，
，
，
，，
，
，
，
，
，
，
，
.
（2）①在中，，
，
，
解这个方程，得.
②如图②所示.
③S△AEF=SABCD- S△ADF - S△ABE - S△EFC
=111---
=111-（DF+BE）11-
=111-EF11-
=111-5y2-（11-x）（11-y1）
=51-xy1
当x=4，y1=4.29时，S△AEF最小
S△AEF=51-×4×.29≈41.4或41.5.
图① 图②
本题为四边形综合题，涉及到三角形全等、函数作图，此类题目通常在作图的基础上，从图表查阅符合条件的数据点，进而求解．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、且
【解析】
分式的分母不等于零时分式有意义，且还需满足被开方数大于等于零的条件，根据要求列式计算即可.
【详解】
∵代数式有意义，
∴，且，
∴且，
故答案为：且.
此题考查分式有意义的条件，二次根式被开方数的取值范围的确定，正确理解题意列出不等式是解题的关键.
20、
【解析】
根据矩形的性质就可以得出EF，AP互相平分，且EF=AP，根据垂线段最短的性质就可以得出AP⊥BC时，AP的值最小，即AM的值最小，由勾股定理求出BC，根据面积关系建立等式求出其解即可．
【详解】
解：∵PE⊥AB，PF⊥AC，∠BAC=90°，
∴∠EAF=∠AEP=∠AFP=90°，
∴四边形AEPF是矩形，
∴EF，AP互相平分．且EF=AP，
∴EF，AP的交点就是M点，
∵当AP的值最小时，AM的值就最小，
∴当AP⊥BC时，AP的值最小，即AM的值最小．
∵AP×BC=AB×AC，
∴AP×BC=AB×AC，
在Rt△ABC中，由勾股定理，得BC==10，
∵AB=6，AC=8，
∴10AP=6×8，
∴AP=
∴AM=，
故答案为：．
考点：(1)、矩形的性质的运用；(2)、勾股定理的运用；(3)、三角形的面积公式
21、9或．
【解析】
分两种情况画图，利用等腰直角三角形的性质和勾股定理矩形计算即可．
【详解】
解：①如图1，延长EA交DC于点F，
∵菱形ABCD的周长为24，
∴AB=BC=6，
∵∠ABC=60°，
∴三角形ABC是等边三角形，
∴∠BAC=60°，
当EA⊥BA时，△ABE是等腰直角三角形，
∴AE=AB=AC=6，∠EAC=90°+60°=150°，
∴∠FAC=30°，
∵∠ACD=60°，
∴∠AFC=90°，
∴CF=AC=3，
则△ACE的面积为：AE×CF=×6×3=9；
②如图2，过点A作AF⊥EC于点F，
由①可知：∠EBC=∠EBA+∠ABC=90°+60°=150°，
∵AB=BE=BC=6，
∴∠BEC=∠BCE=15°，
∴∠AEF=45°-15°=30°，∠ACE=60°-15°=45°，
∴AF=AE，AF=CF=AC=，
∵AB=BE=6，
∴AE=，
∴EF=，
∴EC=EF+FC=
则△ACE的面积为：EC×AF=．
故答案为：9或．
本题考查了菱形的性质、等腰三角形的性质、等边三角形的判定与性质，解决本题的关键是掌握菱形的性质．
22、
【解析】
过点F作AB的垂线，垂足为H，设DF=X，则，C=4，FC=,
，即DF=3，在直角三角形FHE中，
23、1.2
【解析】分析: 先由平均数的公式计算出a的值，再根据方差的公式计算即可．
详解: ∵数据10，9，a，12，9的平均数是10，
∴(10+9+a+12+9)÷5=10，
解得：a=10，
∴这组数据的方差是15[(10−10) ² +(9−10) ² +(10−10) ² +(12−10) ² +(9−10) ²]=1.2.
故选B.
点睛: 本题考查方差和平均数，方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
二、解答题（本大题共3个小题，共30分）
24、（1）CD；平行；（2）见解析；（3）平行四边形的对边相等
【解析】
（1）CD；平行；
（2）证明：连接BD．
在△ABD和△CDB中，
∵AB＝CD，AD＝CB，BD＝DB，
∴△ABD≌△CDB．
∴∠1＝∠2，∠3＝∠4，
∴AB//CD，AD//CB，
∴四边形ABCD是平行四边形．
（3）平行四边形的对边相等
考点：平行四边形的判定，全等三角形的判定
25、①菜地离小明家1.1千米，小明走到菜地用了15分钟；②小明给菜地浇水用了10分钟；③玉米地离菜地、小明家的距离分别为0.9千米，2千米，小明从玉米地走回家平均速度是0.08千米/分钟．
【解析】
①根据函数图象可以直接写出菜地离小明家多远，小明走到菜地用了多少时间；
②根据函数图象中的数据可以得到小明给菜地浇水用了多少时间；
③根据函数图象中的数据可以得到玉米地离菜地、小明家多远，小明从玉米地走回家平均速度是多少．
【详解】
①由图象可得，
菜地离小明家1.1千米，小明走到菜地用了15分钟；
②25-15=10（分钟），
即小明给菜地浇水用了10分钟；
③2-1.1=0.9（千米）
玉米地离菜地、小明家的距离分别为0.9千米，2千米，
小明从玉米地走回家平均速度是2÷（80-55）=0.08千米/分钟．
本题考查函数图象，解答本题的关键是明确题意，利用数形结合的思想解答．
26、（1），；（2）．
【解析】
（1）把A点坐标代入反比例函数的解析式，即可求出反比例函数的解析式，再求出B点坐标，把A、B的坐标代入一次函数的解析式，得出方程组，求出方程组的解，即可得出一次函数的解析式；
（2）由面积的和差关系可求解．
【详解】
（1）∵点A（﹣3，2）在反比例函数y（x＜0）的图象上，∴m=﹣3×2=﹣6，∴反比例函数解析式为：y．
∵点B（n，4）在反比例函数y（x＜0）的图象，∴n，∴点B（，4）．
∵点A，点B在一次函数y=kx+b的图象上，∴，解得：，∴一次函数解析式为：yx+6；
（2）设一次函数与x轴交于点D．在yx+6中，令y=0，解得：x=－4.1．
∵C（－1，0），∴CD=3.1，∴S△ABC = S△DBC－S△ADC==．
本题考查了一次函数和反比例函数的交点问题的应用，三角形的面积，用待定系数法求函数的图象，主要考查学生的计算能力，题目比较好，难度适中．
题号
一
二
三
四
五
总分
得分
批阅人
x
1
1
2
3
4
5
6
7
8
9
11
11
8.18
6.67
5.38
4.29
3.33
a
1.76
1.11
1.53
1