

安徽省合肥市、安庆市名校2024-2025学年数学九上开学经典试题【含答案】
展开一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)函数y=mx+n与y=nx的大致图象是( )
A.B.
C.D.
2、(4分)某灯泡厂为测量一批灯泡的使用寿命,从中抽查了100只灯泡.它们的使用寿命如下表所示:
这批灯泡的平均使用寿命是( )
A.1120小时B.1240小时C.1360小时D.1480小时
3、(4分)下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且平分的四边形是正方形
4、(4分)下列各组线段能构成直角三角形的是( )
A.B.C.D.
5、(4分)的值等于
A.3B.C.D.
6、(4分)下列命题:
①两条直线被第三条直线所截,同位角相等;
②两点之间,线段最短;
③相等的角是对顶角;
④直角三角形的两个锐角互余;
⑤同角或等角的补角相等.
其中真命题的个数是( )
A.2个B.3个C.4个D.5个
7、(4分)已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )
A.3B.4C.5D.6
8、(4分)某班5位学生参加中考体育测试的成绩(单位:分)分别是:50、45、36、48、50,则这组数据的众数是( )
A.36B.45C.48D.50
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)如图,在□ABCD中,AB=5,AD=6,将□ABCD沿AE翻折后,点B恰好与点 C重合,则折痕AE的长为____.
10、(4分)如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为_____.
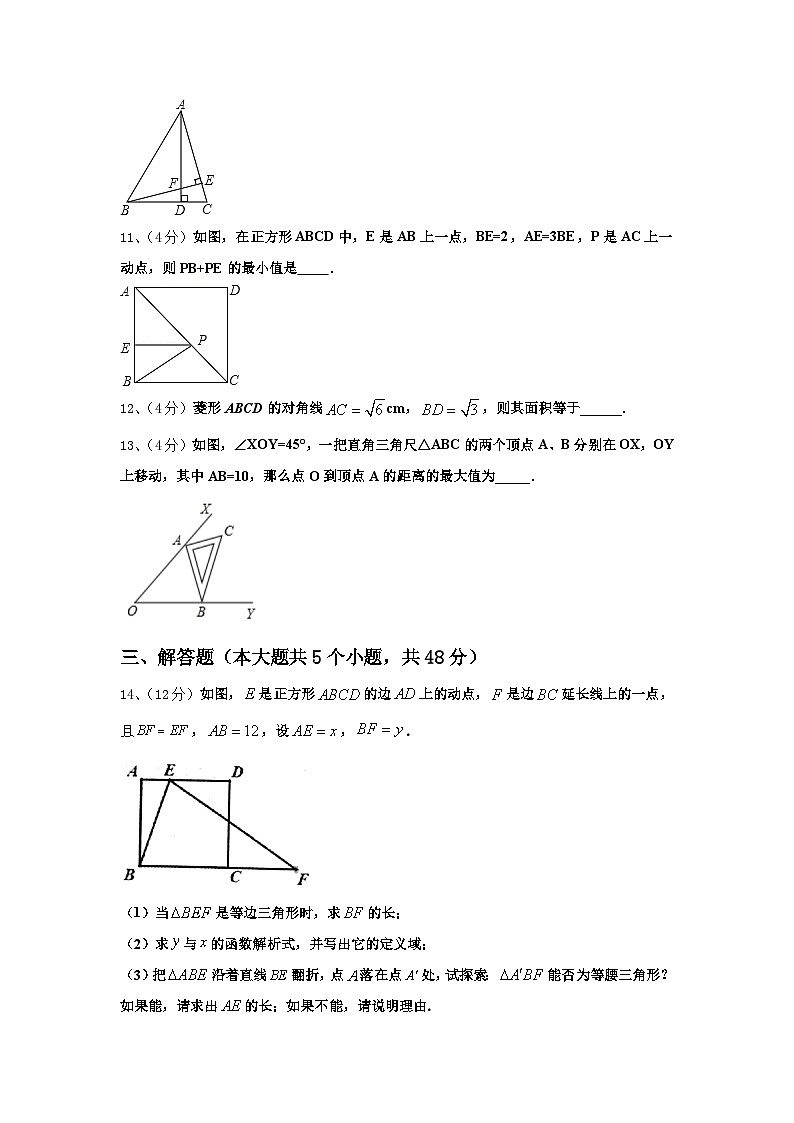
11、(4分)如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
12、(4分)菱形ABCD的对角线cm,,则其面积等于______.
13、(4分)如图,∠XOY=45°,一把直角三角尺△ABC的两个顶点A、B分别在OX,OY上移动,其中AB=10,那么点O到顶点A的距离的最大值为_____.
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,是正方形的边上的动点,是边延长线上的一点,且,,设,.
(1)当是等边三角形时,求的长;
(2)求与的函数解析式,并写出它的定义域;
(3)把沿着直线翻折,点落在点处,试探索:能否为等腰三角形?如果能,请求出的长;如果不能,请说明理由.
15、(8分)将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.
16、(8分)已知a,b是直角三角形的两边,且满足,求此三角形第三边长.
17、(10分)已知点A及第一象限的动点,且,设△OPA的面积为S.
(1)求S关于的函数解析式,并写出的取值范围;
(2)画出函数S的图象,并求其与正比例函数的图象的交点坐标;
(3)当S=12时,求P点坐标.
18、(10分)甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)一次函数y=kx+2(k≠0)的图象与x轴交于点A(n,0),当n>0时,k的取值范围是_____.
20、(4分)某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯顶端距离地面AO=12,梯子底端离墙角的距离BO=5m.亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,请问这个定值是 _______.
21、(4分)分解因式xy2+4xy+4x=_____.
22、(4分)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B5的坐标是_____________ 。
23、(4分)计算: =______________
二、解答题(本大题共3个小题,共30分)
24、(8分)已知求代数式:x=2+,y=2-.
(1)求代数式x2+3xy+y2的值;
(2)若一个菱形的对角线的长分别是x和y,求这个菱形的面积?
25、(10分)如图,在中,按如下步骤作图:
①以点A为圆心,AB长为半径画弧;
②以点C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD、CD;
(1)求证:;
(2)当时,猜想四边形ABCD是什么四边形,并证明你的结论;
(3)当,,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
26、(12分)如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、D
【解析】
当m>0,n>0时,y=mx+n经过一、二、三象限,y=nx经过一、三象限;
当m>0,n<0时,y=mx+n经过一、三、四象限,y=nx经过二、四象限;
当m<0,n>0时,y=mx+n经过一、二、四象限,y=nx经过一、三象限;
当m<0,n<0时,y=mx+n经过二、三、四象限,y=nx经过二、四象限.
综上,A,B,C错误,D正确
故选D.
考点:一次函数的图象
2、B
【解析】
先用每组的组中值表示这组的使用寿命,然后根据加权平均数的定义计算.
【详解】
根据题意得:(800×30+1200×30+1600×40)
=×124000
=1240(h).
则这批灯泡的平均使用寿命是1240h.
故选B.
本题考查了加权平均数:若n个数x1,x2,x3,…,xn的权分别是w1,w2,w3,…,wn,则(x1w1+x2w2+…+xnwn)÷(w1+w2+…+wn)叫做这n个数的加权平均数.
3、D
【解析】
分别利用平行四边形、矩形、菱形和正方形的判定定理,对选项逐一分析即可做出判断.
【详解】
解:A、两组对边分别相等的四边形是平行四边形,符合平行四边形的判定,故本选项正确,不符合题意;
B、∵四边形的内角和为360°,四边形的四个内角都相等,
∴四边形的每个内角都等于90°,则这个四边形有三个角是90°,
∴这个四边形是矩形,故四个内角都相等的四边形是矩形,本选项正确,不符合题意;
C、四条边都相等的四边形是菱形,符合菱形的判定,,故本选项正确,不符合题意;
D、两条对角线垂直且平分的四边形是菱形,不一定是正方形,故本选项错误,符合题意;
故选:D.
本题考查了平行四边形、矩形、菱形和正方形的判定定理,解题的关键是正确理解并掌握判定定理.
4、D
【解析】
欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【详解】
A、12+22≠22,不能构成直角三角形;
B、72+122≠132,不能构成直角三角形;
C、52+82≠102,不能构成直角三角形;
D、,能构成直角三角形.
故选:D.
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.
5、A
【解析】
.故选A.
6、B
【解析】
解:命题①两条平行线被第三条直线所截,同位角相等,错误,为假命题;
命题②两点之间,线段最短,正确,为真命题;
命题③相等的角是对顶角,错误,为假命题;
命题④直角三角形的两个锐角互余,正确,为真命题;
命题⑤同角或等角的补角相等,正确,为真命题,
故答案选B.
考点:命题与定理.
7、C
【解析】
在Rt△ABC中利用勾股定理可求出AC=1,设BE=a,则CE=8﹣a,根据折叠的性质可得出BE=FE=a,AF=AB=6,∠AFE=∠B=90°,进而可得出FC=2,在Rt△CEF中,利用勾股定理可得出关于a的一元二次方程,解之即可得出a值,将其代入8﹣a中即可得出线段CE的长度.
【详解】
解:在Rt△ABC中,AB=6,BC=8,
∴AC=1.
设BE=a,则CE=8﹣a,
根据翻折的性质可知,BE=FE=a,AF=AB=6,∠AFE=∠B=90°,
∴FC=2.
在Rt△CEF中,EF=a,CE=8﹣a,CF=2,
∴CE2=EF2+CF2,即(8﹣a)2=a2+22,
解得:a=3,
∴8﹣a=3.
故选:C.
本题考查了翻折变换、矩形的性质、勾股定理以及解一元二次方程,在Rt△CEF中,利用勾股定理找出关于a的一元二次方程是解题的关键.
8、D
【解析】
根据众数的定义,找出这组数据中出现次数最多的数,即可求出答案.
【详解】
解:在这组数据50、45、36、48、50中,
50出现了2次,出现的次数最多,
则这组数据的众数是50,
故选D.
考查了众数,掌握众数的定义是本题的关键,众数是一组数据中出现次数最多的数.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、1
【解析】
由点B恰好与点C重合,可知AE垂直平分BC,根据勾股定理计算AE的长即可.
【详解】
解:∵翻折后点B恰好与点C重合,
∴AE⊥BC,BE=CE,
∵BC=AD=6,
∴BE=3,
∴AE=.
故答案为:1.
本题考查了翻折变换,平行四边形的性质,勾股定理,根据翻折特点发现AE垂直平分BC是解决问题的关键.
10、1
【解析】
分析:首先证明△AEF≌△BEC,推出AF=BC=10,设DF=x.由△ADC∽△BDF,推出,构建方程求出x即可解决问题;
详解:∵AD⊥BC,BE⊥AC,
∴∠AEF=∠BEC=∠BDF=90°,
∵∠BAC=45°,
∴AE=EB,
∵∠EAF+∠C=90°,∠CBE+∠C=90°,
∴∠EAF=∠CBE,
∴△AEF≌△BEC,
∴AF=BC=10,设DF=x.
∵△ADC∽△BDF,
∴,
∴,
整理得x2+10x﹣24=0,
解得x=2或﹣12(舍弃),
∴AD=AF+DF=12,
∴S△ABC=•BC•AD=×10×12=1.
故答案为1.
点睛:本题考查勾股定理、等腰三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会利用参数构建方程解决问题,属于中考常考题型.
11、10
【解析】
由正方形性质的得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.
【详解】
如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小.
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,
∴AE=6,AB=8,
∴DE==10,
故PB+PE的最小值是10.
故答案为10.
12、
【解析】
根据菱形的性质,菱形的面积等于两条对角线乘积的一半,代入数值计算即可。
【详解】
解:菱形ABCD的面积=
=
=
本题考查了菱形的性质:菱形的面积等于两条对角线乘积的一半。
13、10
【解析】
当∠ABO=90°时,点O到顶点A的距离的最大,则△ABC是等腰直角三角形,据此即可求解.
【详解】
解:∵
∴当∠ABO=90°时,点O到顶点A的距离最大.
则OA=AB=10.
故答案是:10.
本题主要考查了等腰直角三角形的性质,正确确定点O到顶点A的距离的最大的条件是解题关键.
三、解答题(本大题共5个小题,共48分)
14、(1);(1);(3)答案见解析.
【解析】
(1)当△BEF是等边三角形时,有∠ABE=∠ABC-∠EBC=90°-60°=30°,则可解Rt△ABE,求得BF即BE的长.
(1)作EG⊥BF,垂足为点G,则四边形AEGB是矩形,在Rt△EGF中,由勾股定理知,EF1=(BF-BG)1+EG1.即y1=(y-x)1+111.故可求得y与x的关系.
(3)当把△ABE沿着直线BE翻折,点A落在点A'处,应有∠BA'F=∠BA'E=∠A=90°,若△A'BF成为等腰三角形,必须使A'B=A'F=AB=11,有FA′=EF-A′E=y-x=11,故可由(1)得到的y与x的关系式建立方程组求得AE的值.
【详解】
解:(1)当是等边三角形时,,
∵,
∴,
∴;
(1)作,垂足为点,
根据题意,得,,.
∴.
∴所求的函数解析式为;
(3)∵,
∴点落在上,
∴,,
∴要使成为等腰三角形,必须使.
而,,
∴,由(1)关系式可得:,
整理得,
解得,
经检验:都原方程的根,
但不符合题意,舍去,
所以当时,为等要三角形.
本题利用了等边三角形和正方形、矩形、等腰三角形的性质,勾股定理求解.
15、(1)①证明见解析;②证明见解析;(2)
【解析】
(1)①首先证明△ABA1是等边三角形,可得∠AA1B=∠A1BD1=60°,即可解决问题.
②首先证明△OCD1≌△OBA(AAS),推出OC=OB,再证明△DCO≌△ABO(SAS)即可解决问题.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.利用勾股定理求出AE,A1E即可解决问题.
【详解】
(1)证明:①如图1中,
∵∠BAC=60°,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=60°,
∴∠AA1B=∠A1BD1,
∴AC∥BD1,
∵AC=BD1,
∴四边形ABD1C是平行四边形.
②如图2中,连接BD1.
∵四边形ABD1C是平行四边形,
∴CD1∥AB,CD1=AB,
∠OCD1=∠ABO,
∵∠COD1=∠AOB,
∴△OCD1≌△OBA(AAS),
∴OC=OB,
∵CD=BA,∠DCO=∠ABO,
∴△DCO≌△ABO(SAS),
∴DO=OA.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.
在Rt△A1BC中,∵∠CA1B=90°,BC=2.AB=3,
∴CA1==4,
∵•A1C•A1B=•BC•A1F,
∴A1F=,
∵∠A1FB=∠A1EB=∠EBF=90°,
∴四边形A1EBF是矩形,
∴EB=A1F=,A1E=BF=,
∴AE=3﹣=,
在Rt△AA1E中,AA1==.
本题属于四边形综合题,考查了矩形的性质,全等三角形的判断和性质,勾股定理,平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题.
16、3或
【解析】
分析:先把右边的项移到左边,,根据完全平方公式变形为,根据算术平方根的非负性和偶次方的非负性列方程求出a、b的值,然后分两种情况利用勾股定理求第三边的长.
详解:由=8b-b2-16,
得-8b+b2+16=0,
得+(b-4)2=0.
又∵≥0,且(b-4)2≥0,
∴a-5=0,b-4=0,
∴a=5,b=4,
当a、b为直角边时,
第三边=;
当a为斜边时,
第三边=;
点睛:本题考查了算术平方根的非负性,偶次方的非负性,完全平方公式,勾股定理及分类讨论的数学思想. 分两种情况求解是正确解答本题的关键.
17、(1)S=-4x+40 (0<x<10);(2)(,);(3)P(7,3)
【解析】
(1)根据△OAP的面积=OA×y÷2列出函数解析式,及点P(x,y)在第一象限内求出自变量的取值范围.
(2)根据S=-4x+40画出函数图像,并与正比例函数S=2x联立方程组,即可求出交点坐标.
(3)将S=12代入(1)求出的解析式中即可.
【详解】
解:(1)依题意有S=×8×(10-x)=-4x+40,
∵点P(x,y)在第一象限内,
∴x>0,y=10-x>0,
解得:0<x<10,
故关于x的函数解析式为:S=-4x+40 (0<x<10);
(2)∵解析式为S=-4x+40(0<x<10);
∴函数图象经过点(10,0)(0,40)(但不包括这两点的线段).
所画图象如下:
令,
解得,
所以交点坐标为(,);
(3)将S=12代入S=-4x+40,
得:12=-4x+40,
解得:x=7,
故点P(7,3).
本题考查的是一次函数的性质,熟知一次函数的图象与系数的关系是解答此题的关键.
18、(1)y=1x﹣120;(2)两车在途中第二次相遇时它们距出发地的路程为240千米;
(3)乙车出发1小时,两车在途中第一次相遇.
【解析】
分析:(1)由图可看出,乙车所行路程y与时间x的成一次函数,使用待定系数法可求得一次函数关系式;
(2)由图可得:交点F表示第二次相遇,F点横坐标为6,代入(1)中的函数即可求得距出发地的路程;
(3)交点P表示第一次相遇,即甲车故障停车检修时相遇,点P的横坐标表示时间,纵坐标表示离出发地的距离,要求时间,则需要把点P的纵坐标先求出;从图中看出,点P的纵坐标与点B的纵坐标相等,而点B在线段BC上,BC对应的函数关系可通过待定系数法求解,点B的横坐标已知,则纵坐标可求.
详解:(1)设乙车所行使路程y与时间x的函数关系式为y=k1x+b1,把(2,0)和(10,480)代入,得:,
解得:,
故y与x的函数关系式为y=1x﹣120;
(2)由图可得:交点F表示第二次相遇,F点的横坐标为6,此时y=1×6=120=240,则F点坐标为(6,240),故两车在途中第二次相遇时它们距出发地的路程为240千米;
(3)设线段BC对应的函数关系式为y=k2x+b2,把(6,240)、(8,480)代入,得:
,
解得:,
故y与x的函数关系式为y=120x﹣480,则当x=4.5时,y=120×4.5﹣480=1.
可得:点B的纵坐标为1.
∵AB表示因故停车检修,∴交点P的纵坐标为1,把y=1代入y=1x﹣120中,有1=1x﹣120,解得x=3,则交点P的坐标为(3,1).
∵交点P表示第一次相遇,∴乙车出发3﹣2=1小时,两车在途中第一次相遇.
点睛:本题意在考查学生利用待定系数法求解一次函数关系式,并利用关系式求值的运算技能和从坐标系中提取信息的能力,是道综合性较强的代数应用题,对学生能力要求比较高.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、k<1
【解析】
分析:根据题意可以用含k的式子表示n,从而可以得出k的取值范围.
详解:∵一次函数y=kx+2(k≠1)的图象与x轴交于点A(n,1),
∴n=﹣,
∴当n>1时,﹣>1,
解得,k<1,
故答案为k<1.
点睛:本题考查一次函数图象与系数的关系,解答本题的关键是明确题意,利用一次函数的性质和不等式的性质解答.
20、
【解析】
根据勾股定理求出AB的长度,然后由直角三角形斜边上的中线的性质回答问题.
【详解】
解:在Rt△ABO中,AO=12,BO=5,
∴,
∵直角三角形斜边上的中线等于斜边的一半,
∴AB上的中点到墙角O的距离总是定值,
此定值为.
故答案为:.
本题考查了勾股定理的应用,以及斜边上的中线等于斜边的一半,解题的关键是在直角三角形中弄清直角边和斜边.
21、x(y+2)2
【解析】
原式先提取x,再利用完全平方公式分解即可。
【详解】
解:原式=,故答案为:x(y+2)2
此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
22、(31,16)
【解析】
首先由B1的坐标为(1,1),点B2的坐标为(3,2),可得正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2,即可求得A1的坐标是(0,1),A2的坐标是:(1,2),然后又待定系数法求得直线A1A2的解析式,由解析式即可求得点A3的坐标,继而可得点B3的坐标,观察可得规律Bn的坐标是(2n-1,2n-1).
【详解】
∵B1的坐标为(1,1),点B2的坐标为(3,2)
∴正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2
∴A1的坐标是(0,1),A2的坐标是:(1,2)
设直线A1A2的解析式为:y=kx+b
∴
解得:
∴直线A1A2的解析式是:y=x+1
∵点B2的坐标为(3,2)
∴点A3的坐标为(3,4)
∴点B3的坐标为(7,4)
∴Bn的横坐标是:2n-1,纵坐标是:2n−1
∴Bn的坐标是(2n−1,2n−1)
故点B5的坐标为(31,16).
此题考查了待定系数法求解一次函数的解析式以及正方形的性质,在解题中注意掌握数形结合思想与方程思想的应用.
23、2
【解析】
先将二次根式化为最简,然后合并同类二次根式即可.
【详解】
解:原式=.
故答案为:2.
本题考查了二次根式的加减运算,掌握二次根式的化简及同类二次根式的合并是关键.
二、解答题(本大题共3个小题,共30分)
24、(1)18;(2)1.
【解析】
(1)求出x+y,xy的值,利用整体的思想解决问题;
(2)根据菱形的面积等于对角线乘积的一半计算即可.
解:(1)∵x=,y=,
∴x+y=4,xy=4-2=2
∴x2+3xy+y2=(x+y)2+xy
=16+2
=18
(2)S菱形=xy==(4-2) =1
“点睛”本题考查菱形的性质,二次根式的加减乘除运算法则等知识,解题的关键是学会整体的思想进行化简计算,属于中考常考题型.
25、(1)证明见解析(2)四边形ABCD是菱形(3)
【解析】
(1)依据条件证即可;
(2)依据四条边都相等的四边形是菱形判定即可;
(3)割补后,图形的面积不变,故正方形的面积就等于菱形的面积,求出菱形面积即可得正方形的边长.
【详解】
(1)证明:在和中,,
,
;
(2)解:四边形ABCD是菱形,理由如下:
,,,
,
四边形ABCD是菱形;
(3)解:,,
,
四边形ABCD的面积,
拼成的正方形的边长.
本题主要考查了三角形的全等的证明、菱形的判定、正方形的性质,正确理解作图步骤获取有用条件是解题的关键.
26、 (1)见解析;(2);(3)见解析
【解析】
试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;
(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
试题解析:(1)证明:连接AC,
∵∠1+∠2=60°,∠3+∠2=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=∠ADC=60°
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴△ABC、△ACD为等边三角形
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF.(ASA)
∴BE=CF.
(2)解:由(1)得△ABE≌△ACF,
则S△ABE=S△ACF.
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,
是定值.
作AH⊥BC于H点,
则BH=2,
S四边形AECF=S△ABC
=
=
=;
(3)解:由“垂线段最短”可知,
当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的面积会随着AE的变化而变化,且当AE最短时,
正三角形AEF的面积会最小,
又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.
由(2)得,S△CEF=S四边形AECF﹣S△AEF
=﹣=.
点睛:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE≌△ACF是解题的关键.
题号
一
二
三
四
五
总分
得分
批阅人
使用寿命x/小时
600≤x≤1000
1000≤x≤1400
1400≤x≤1800
灯泡数/个
30
30
40
安徽省合肥市46中学2024-2025学年九上数学开学考试试题【含答案】: 这是一份安徽省合肥市46中学2024-2025学年九上数学开学考试试题【含答案】,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
安徽省合肥市、安庆市名校2024年数学九年级第一学期开学检测试题【含答案】: 这是一份安徽省合肥市、安庆市名校2024年数学九年级第一学期开学检测试题【含答案】,共25页。试卷主要包含了选择题,四象限D.当x=时,y=1,解答题等内容,欢迎下载使用。
安徽省安庆市区二十三校2024-2025学年数学九上开学联考模拟试题【含答案】: 这是一份安徽省安庆市区二十三校2024-2025学年数学九上开学联考模拟试题【含答案】,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












