江苏省无锡市梁溪区江南中学2023-2024学年七年级上学期期中数学试卷

这是一份江苏省无锡市梁溪区江南中学2023-2024学年七年级上学期期中数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）2023的相反数是（ ）
A．B．C．2023D．﹣2023
2．（3分）平方得64的所有数是（ ）
A．﹣8B．±8C．±4D．+8
3．（3分）正负数可以表示一组具有相反意义的量，如果将小明在图书馆借书10本记作+10，那么还书5本可以记作（ ）
A．﹣10B．+10C．﹣5D．+5
4．（3分）若5x2ay和3x2y是同类项，则a的值为（ ）
A．0B．1C．2D．3
5．（3分）下列计算正确的是（ ）
A．﹣ab+ab＝0B．3a+2b＝5ab
C．3a2+4b2＝7D．3ab﹣2ba＝5ab
6．（3分）下列说法中正确的是（ ）
A．单项式2x的系数是2
B．xy2+x﹣1是三次二项式
C．﹣的系数是﹣
D．23xy2的次数是6
7．（3分）在﹣6.7，0，0.1010010001…，π，0.156156这五个数中，无理数的个数为（ ）
A．0B．1C．2D．3
8．（3分）当x＝2时，代数式ax3﹣bx+1的值为10，则当x＝﹣2时这个代数式的值为（ ）
A．10B．﹣10C．8D．﹣8
9．（3分）有理数m、n在数轴上对应点的位置如图，则m、n、|n|、﹣m、0的大小关系是（ ）
A．n＜0＜﹣m＜m＜|n|B．n＜﹣m＜0＜|n|＜m
C．n＜|n|＜0＜﹣m＜mD．n＜﹣m＜0＜m＜|n|
10．（3分）如图，点O为原点，A、B为数轴上两点，AB＝15，且OA＝2OB，点P从点B开始以每秒4个单位的速度向右运动，当点P开始运动时，点A、B分别以每秒5个单位和每秒2个单位的速度同时向右运动，设运动时间为t秒，若2AP+3OP﹣mBP的值在某段时间内不随着t的变化而变化，则m的值为（ ）
A．5B．5或7C．3或5D．3或7
二、填空题（本大题共8小题，每小题3分，共24分;不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）
11．（3分）试写出一个含x的代数式 ，使得当x＝4时，代数式的值为﹣12．
12．（3分）数轴上表示数﹣5和表示数﹣9的两点之间的距离是 ．
13．（3分）据统计，2023年中秋国庆假期，全国国内旅游出游预计将达到896000000人次．数据896000000用科学记数法表示为 ．
14．（3分）若a、b满足等式a2+2ab+b2＝3，a2﹣2ab+b2＝7，则ab＝ ．
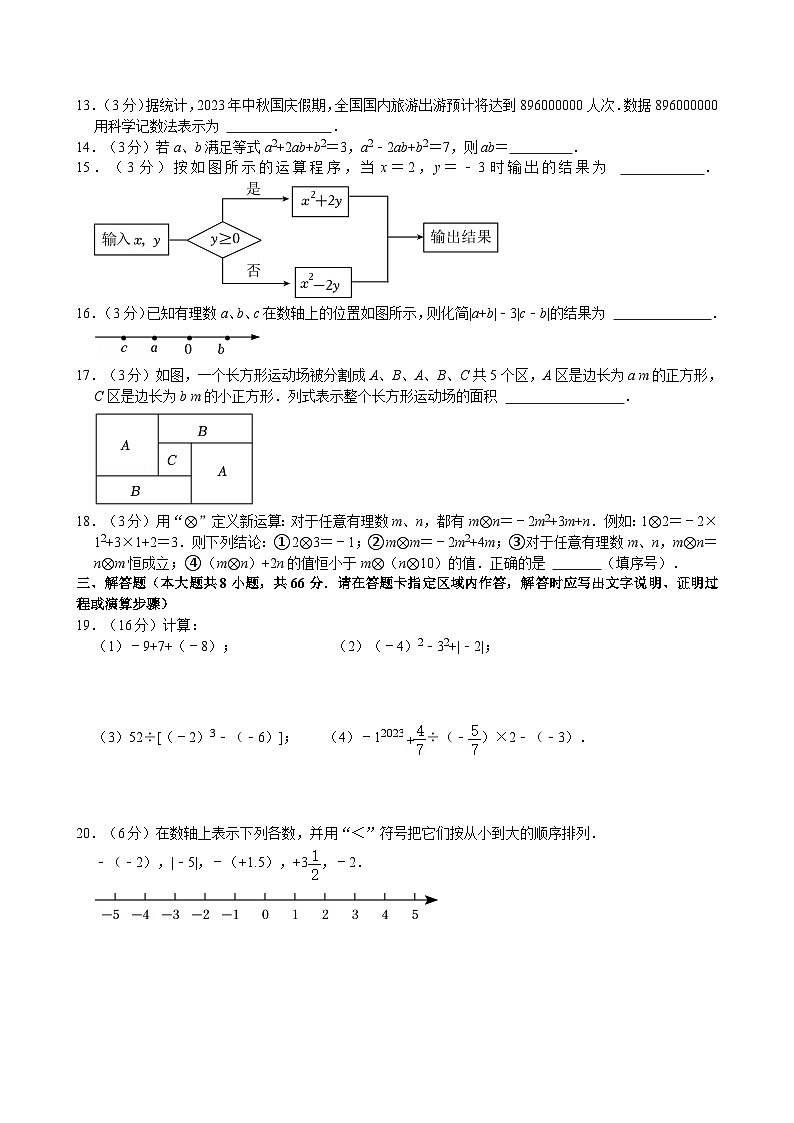
15．（3分）按如图所示的运算程序，当x＝2，y＝﹣3时输出的结果为 ．
16．（3分）已知有理数a、b、c在数轴上的位置如图所示，则化简|a+b|﹣3|c﹣b|的结果为 ．
17．（3分）如图，一个长方形运动场被分割成A、B、A、B、C共5个区，A区是边长为a m的正方形，C区是边长为b m的小正方形．列式表示整个长方形运动场的面积 ．
18．（3分）用“⊗”定义新运算：对于任意有理数m、n，都有m⊗n＝﹣2m2+3m+n．例如：1⊗2＝﹣2×12+3×1+2＝3．则下列结论：①2⊗3＝﹣1；②m⊗m＝﹣2m2+4m；③对于任意有理数m、n，m⊗n＝n⊗m恒成立；④（m⊗n）+2n的值恒小于m⊗（n⊗10）的值．正确的是 （填序号）．
三、解答题（本大题共8小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（16分）计算：
（1）﹣9+7+（﹣8）； （2）（﹣4）2﹣32+|﹣2|；
（3）52÷[（﹣2）3﹣（﹣6）]； （4）﹣12023÷（﹣）×2﹣（﹣3）．
20．（6分）在数轴上表示下列各数，并用“＜”符号把它们按从小到大的顺序排列．
﹣（﹣2），|﹣5|，﹣（+1.5），+3，﹣2．
21．（8分）化简：
（1）2m3﹣（+2m2）﹣（﹣3m2）+3m3+m； （2）（3x2﹣4xy）﹣2（﹣2xy+y2）．
22．（5分）先化简，后求值：3ab2﹣（ab+2ab2）+4ab，其中|a﹣1|+（b+2）2＝0．
23．（5分）已知a、b互为相反数，c、d互为倒数，|m|＝1，求﹣2cd+m2的值．
24．（8分）水果超市最近新进了一批橙子，每斤进价10元，9月29日每斤售价15元，国庆黄金周9月30日起试行机动价格，价格超出前一天的部分记为正，不足前一天的部分记为负，超市记录了国庆黄金周橙子的售价变化情况和售出情况：
（1）10月4日超市售出的橙子的单价是多少元？
（2）10月4日超市售出的橙子的收益如何？（盈利或亏损的钱数）
（3）国庆黄金周水果超市出售此种橙子的收益如何？
25．（8分）相较于自己做一顿饭较高的时间成本，点外卖不仅可以节省大量的时间，也可以满足年轻人对于“吃”的需求．某餐厅打算在美团和饿了么平台根据点餐金额采用不同的优感惠策略，在美团平台实施方案如下：
在饿了么平台实施方案如下：
（1）若小华点餐金额为60元，那么在美团和饿了么平台上的实际付款金额分别是多少？
（2）若小华点餐金额为n元（n＞158），那么小华在美团和饿了么平台上的实际付款金额分别是多少？（用含n的代数式表示）
（3）若小华在两个平台各点单一次，两次点餐金额共300元．其中美团点餐金额比饿了么点餐金额低，设美团的点餐金额是x元，求两次实际付款金额共多少？（用含x的代数式表示）
26．（10分）小明在一条长方形的纸带上画了一条数轴，进行操作井研究．
（1）操作1：折叠纸带，使数轴上表示1的点与表示﹣1的点重合，则表示数﹣2的点与表示数 的点重合．
（2）操作2：折叠纸带，使数轴上表示1的点与表示﹣5的点重合，则表示数a的点与表示数 的点重合．
（3）操作3：如图，在数轴上剪下6个单位长度（从﹣1到5）的一条线段，并把这条线段沿某点向左对折，然后在重叠部分的某处剪一刀得到三条线段，若这三条线段的长度之比为1：2：2，则折痕处对应的点表示的数可能是几？
附加题（本题10分）
27．（﹣1）2＝ .（﹣1）3＝ ．
28．计算（﹣1）n．
29．桌子上有7只杯口朝上的茶杯，每次翻转2只，能否经过若干次翻转使7只杯口全部朝下？若用“+1”、“﹣1”分别表示“朝上”、“朝下”，请用有理数的运算说明理由．
30．桌子上有23只杯口朝上的茶杯，每次翻转3只，经过20次翻转 使23只杯口全部朝下．（填“能”或“不能”）
2023-2024学年江苏省无锡市梁溪区江南中学七年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分．在每小题所给出的四个选项中，只有一项是正确的，只需把答案直接填写在答卷上相应的位置）
1．（3分）2023的相反数是（ ）
A．B．C．2023D．﹣2023
【分析】只有符号不同的两个数叫做互为相反数，由此即可得到答案．
【解答】解：2023的相反数是﹣2023．
故选：D．
【点评】本题考查相反数，关键是掌握相反数的定义．
2．（3分）平方得64的所有数是（ ）
A．﹣8B．±8C．±4D．+8
【分析】根据有理数的乘方的定义解答即可．
【解答】解：∵（±8）2＝64，
∴平方得64的数是±8，
故选：B．
【点评】本题考查了有理数的乘方，熟知有理数的乘方的定义是解题的关键．
3．（3分）正负数可以表示一组具有相反意义的量，如果将小明在图书馆借书10本记作+10，那么还书5本可以记作（ ）
A．﹣10B．+10C．﹣5D．+5
【分析】正数和负数是一组具有相反意义的量，据此即可求得答案．
【解答】解：借书10本记作+10，那么还书5本可以记作﹣5，
故选：C．
【点评】本题考查正数和负数，理解具有相反意义的量是解题的关键．
4．（3分）若5x2ay和3x2y是同类项，则a的值为（ ）
A．0B．1C．2D．3
【分析】所含字母相同，并且相同字母的指数也相同，这样的项叫做同类项，由此即可得到答案．
【解答】解：∵5x2ay和3x2y是同类项，
∴2a＝2，
解得a＝1．
故选：B．
【点评】本题考查同类项，关键是掌握同类项的定义．
5．（3分）下列计算正确的是（ ）
A．﹣ab+ab＝0B．3a+2b＝5ab
C．3a2+4b2＝7D．3ab﹣2ba＝5ab
【分析】直接利用合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变，进而得出答案．
【解答】解：A．﹣ab+ab＝0，故此选项符合题意；
B．3a与2b无法合并，故此选项不合题意；
C．3a2与4b2无法合并，故此选项不合题意；
D．3ab﹣2ba＝ab，故此选项不合题意．
故选：A．
【点评】此题主要考查了合并同类项，正确掌握相关运算法则是解题关键．
6．（3分）下列说法中正确的是（ ）
A．单项式2x的系数是2
B．xy2+x﹣1是三次二项式
C．﹣的系数是﹣
D．23xy2的次数是6
【分析】根据多项式和单项式的意义，逐一判断即可解答．
【解答】解：A、单项式2x的系数是2，故A符合题意；
B、xy2+x﹣1是三次三项式，故B不符合题意；
C、﹣的系数是﹣，故C不符合题意；
D、23xy2的次数是3，故D不符合题意；
故选：A．
【点评】本题考查了多项式，单项式，熟练掌握多项式和单项式的意义是解题的关键．
7．（3分）在﹣6.7，0，0.1010010001…，π，0.156156这五个数中，无理数的个数为（ ）
A．0B．1C．2D．3
【分析】无理数即无限不循环小数，据此进行判断即可．
【解答】解：0.1010010001…，π是无限不循环小数，它们是无理数，共2个，
故选：C．
【点评】本题考查无理数的识别，熟练掌握其定义是解题的关键．
8．（3分）当x＝2时，代数式ax3﹣bx+1的值为10，则当x＝﹣2时这个代数式的值为（ ）
A．10B．﹣10C．8D．﹣8
【分析】首先根据当x＝2时，代数式ax3﹣bx+1的值为10得8a﹣2b＝9，然后将x＝﹣2及8a﹣2b＝9代入代数式ax3﹣bx+1之中即可得出答案．
【解答】解：∵当x＝2时，代数式ax3﹣bx+1的值为10，
∴当x＝2时，a×23﹣b×2+1＝10，
整理得：8a﹣2b＝9，
当x＝﹣2时，
ax3﹣bx+1
＝a×（﹣2）3﹣b×（﹣2）+1
＝﹣8a+2b+1
＝﹣（8a﹣2b）+1
＝﹣9+1
＝﹣8．
故选：D．
【点评】此题主要考查了求代数式的值，熟练掌握求代数式值的方法与技巧，理解整体思想的应用是解决问题的关键．
9．（3分）有理数m、n在数轴上对应点的位置如图，则m、n、|n|、﹣m、0的大小关系是（ ）
A．n＜0＜﹣m＜m＜|n|B．n＜﹣m＜0＜|n|＜m
C．n＜|n|＜0＜﹣m＜mD．n＜﹣m＜0＜m＜|n|
【分析】根据理数m、n在数轴上对应点的位置得：n＜0＜m，且|n|＞n，然后在数轴上表示出n，﹣m，m，|n|，再根据“在数轴上左边的点表示的数小于右边的点表示的数”即可得出答案．
【解答】解：根据理数m、n在数轴上对应点的位置得：n＜0＜m，且|n|＞n，
∴有理数n，﹣m，m，|n|在数轴上的位置如图所示：

根据“在数轴上左边的点表示的数小于右边的点表示的数”得：n＜﹣m＜0＜m＜|n|．
故选：D．
【点评】此题主要考查了有理数与数轴，熟练掌握用数轴上的点表示有理数，理解“在数轴上左边的点表示的数小于右边的点表示的数”是解决问题的关键．
10．（3分）如图，点O为原点，A、B为数轴上两点，AB＝15，且OA＝2OB，点P从点B开始以每秒4个单位的速度向右运动，当点P开始运动时，点A、B分别以每秒5个单位和每秒2个单位的速度同时向右运动，设运动时间为t秒，若2AP+3OP﹣mBP的值在某段时间内不随着t的变化而变化，则m的值为（ ）
A．5B．5或7C．3或5D．3或7
【分析】设经过t秒，可得AP＝|5+4t﹣（﹣10+5t）|＝|15﹣t|，OP＝5+4t，BP＝5+4t﹣（5+2t）＝2t，分类讨论t的取值范围，得出2AP+3OP﹣mBP关于t的不同表达形式，可知当t的系数为0时，3AP+2OP﹣mBP的值在某段时间内不随着t的变化而变化．
【解答】解：∵AB＝15，0A＝2OB，
∴OA＝10，OB＝5．
∴A点对应数为﹣10，B点对应数为5，
设运动时间为t秒，
AP＝|5+4t﹣（﹣10+5t）|
＝|15﹣t|，
OP＝5+4t，
BP＝5+4t﹣（5+2t）＝2t，
①当t≤15时，
2AP+3OP﹣mBP
＝30﹣2t+15+12t﹣2mt
＝（10﹣2m）t+45，
当10﹣2m＝0，即m＝5时，
2AP+3OP﹣mBP的值为定值45，在某段时间内不随着t的变化而变化．
②当t＞15时，
2AP+3OP﹣mBP
＝2t﹣30+15+12t﹣2mt
＝（14﹣2m）t﹣15，
当14﹣2m＝0，即m＝7时，
2AP+3OP﹣mBP的值为定值﹣15，在某段时间内不随着t的变化而变化．
故m为5或7．
故选：B．
【点评】本题考查了数轴，解题的关键是读懂题意，用含字母的式子表示点运动后表示的数．
二、填空题（本大题共8小题，每小题3分，共24分;不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）
11．（3分）试写出一个含x的代数式 ﹣3x（答案不唯一） ，使得当x＝4时，代数式的值为﹣12．
【分析】根据题意写出一个符合题意的代数式即可．
【解答】解：当x＝4时，
﹣3x＝﹣3×4＝﹣12，
故答案为：﹣3x（答案不唯一）．
【点评】本题考查代数式求值，此题的答案不唯一，符合题意即可．
12．（3分）数轴上表示数﹣5和表示数﹣9的两点之间的距离是 4 ．
【分析】本题为数轴中的数形结合思想题型；﹣5﹣（﹣9）得出结果即可．
【解答】解：﹣5﹣（﹣9）
＝﹣5+9
＝4
故答案为：4．
【点评】本题考查了数轴中的数形结合思想，符号意识是解题关键．
13．（3分）据统计，2023年中秋国庆假期，全国国内旅游出游预计将达到896000000人次．数据896000000用科学记数法表示为 8.96×108 ．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：896000000＝8.96×108．
故答案为：8.96×108．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
14．（3分）若a、b满足等式a2+2ab+b2＝3，a2﹣2ab+b2＝7，则ab＝ ﹣1 ．
【分析】用第一个式子减去第二个式子后整理并计算即可．
【解答】解：已知a2+2ab+b2＝3①，a2﹣2ab+b2＝7②，
则①﹣②得：4ab＝﹣4，
解得：ab＝﹣1，
故答案为：﹣1．
【点评】本题考查完全平方公式，将两式作差后得到4ab＝﹣4是解题的关键．
15．（3分）按如图所示的运算程序，当x＝2，y＝﹣3时输出的结果为 10 ．
【分析】根据题意列式计算即可．
【解答】解：当x＝2，y＝﹣3时，
∵﹣3＜0，
∴x2﹣2y＝22﹣2×（﹣3）＝4+6＝10，
故答案为：10．
【点评】本题考查代数式求值及有理数的运算，由题意将已知数值代入正确的代数式是解题的关键．
16．（3分）已知有理数a、b、c在数轴上的位置如图所示，则化简|a+b|﹣3|c﹣b|的结果为 a﹣2b+3c ．
【分析】先通过点在数轴上的位置，先判断a、b、c的正负，再根据加法法则、减法法则判断a+b、c﹣b的正负，最后利用绝对值的意义对代数式化简．
【解答】解：由数轴知，c＜a＜0＜b，|a|＜|b|＜|c|，
∴a+b＞0，c﹣b＜0，
∴|a+b|﹣3|c﹣b|＝a+b﹣3（b﹣c）
＝a+b﹣3b+3c
＝a﹣2b+3c．
故答案为：a﹣2b+3c．
【点评】本题考查了数轴、绝对值的有关内容，解决本题的关键是通过数轴，利用加减法法则判断a+b、c﹣b的正负．
17．（3分）如图，一个长方形运动场被分割成A、B、A、B、C共5个区，A区是边长为a m的正方形，C区是边长为b m的小正方形．列式表示整个长方形运动场的面积 （4a2﹣b2）m2 ．
【分析】根据题意和图形，可以得到B区的长为（a+b）m，宽为（a﹣b）m，然后即可表示出整个长方形运动场的面积．
【解答】解：由图可得，
B区的长为（a+b）m，宽为（a﹣b）m，
则整个长方形运动场的面积为：2a2+b2+（a+b）（a﹣b）×2
＝2a2+b2+2a2﹣2b2
＝（4a2﹣b2）m2，
故答案为：（4a2﹣b2）m2．
【点评】本题考查列代数式，解答本题的关键是明确题意，利用数形结合的思想解答．
18．（3分）用“⊗”定义新运算：对于任意有理数m、n，都有m⊗n＝﹣2m2+3m+n．例如：1⊗2＝﹣2×12+3×1+2＝3．则下列结论：①2⊗3＝﹣1；②m⊗m＝﹣2m2+4m；③对于任意有理数m、n，m⊗n＝n⊗m恒成立；④（m⊗n）+2n的值恒小于m⊗（n⊗10）的值．正确的是 ② （填序号）．
【分析】根据新运算列式计算后进行逐项判断即可．
【解答】解：2⊗3＝﹣2×22+3×2+3＝﹣8+6+3＝1，则①错误；
m⊗m＝﹣2m2+3m+m＝﹣2m2+4m，则②正确；
m⊗n＝﹣2m2+3m+n，n⊗m＝﹣2n2+3n+m，两式不一定相等，则③错误；
∵n⊗10＝﹣2n2+3n+10，
∴m⊗（n⊗10）＝﹣2m2+3m﹣2n2+3n+10，
∵（m⊗n）+2n＝﹣2m2+3m+n+2n＝﹣2m2+3m+3n，
∴（m⊗n）+2n﹣m⊗（n⊗10）
＝﹣2m2+3m+3n﹣（﹣2m2+3m﹣2n2+3n+10）
＝﹣2m2+3m+3n+2m2﹣3m+2n2﹣3n﹣10
＝2n2﹣10，
∵2n2﹣10不一定小于0，
∴（m⊗n）+2n的值不一定小于m⊗（n⊗10）的值，
则④错误；
综上，正确的是②，
故答案为：②．
【点评】本题考查有理数的运算，根据定义的新运算列得正确的算式是解题的关键．
三、解答题（本大题共8小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（16分）计算：
（1）﹣9+7+（﹣8）；
（2）（﹣4）2﹣32+|﹣2|；
（3）52÷[（﹣2）3﹣（﹣6）]；
（4）﹣12023÷（﹣）×2﹣（﹣3）．
【分析】（1）根据有理数的加减法法则计算即可；
（2）先计算乘方和去绝对值符号，再计算加减法即可；
（3）先计算乘方，再计算乘除，后计算加减，有括号的先计算括号内的；
（4）先计算乘方，再计算乘除，后计算加减即可．
【解答】解：（1）﹣9+7+（﹣8）
＝﹣2﹣8
＝﹣10；
（2）（﹣4）2﹣32+|﹣2|
＝16﹣9+2
＝7+2
＝9；
（3）52÷[（﹣2）3﹣（﹣6）]
＝52÷（﹣8+6）
＝52÷（﹣2）
＝﹣26；
（4）﹣12023÷（﹣）×2﹣（﹣3）
＝﹣1++3
＝﹣1﹣+3
＝3﹣1﹣
＝2﹣
＝．
【点评】本题考查了有理数的混合运算，掌握相关运算法则是解答本题的关键．
20．（6分）在数轴上表示下列各数，并用“＜”符号把它们按从小到大的顺序排列．
﹣（﹣2），|﹣5|，﹣（+1.5），+3，﹣2．
【分析】首先化简﹣（﹣2）＝2，|﹣5|＝5，﹣（+1.5）＝﹣1.5，然后将它们在数轴上表示出来；再根据在数轴上左边的点表示的数小于右边点表示的数即可将它们用“＜”连接起来．
【解答】解：∵﹣（﹣2）＝2，|﹣5|＝5，﹣（+1.5）＝﹣1.5，
∴﹣（﹣2），|﹣5|，﹣（+1.5），+3，﹣2在数轴上表示如图所示：
∴﹣2＜﹣（+1.5）＜﹣（﹣2）＜+3＜|﹣5|．
【点评】此题主要考查了算术平方根的意义，数轴与有理数，熟练掌握在数轴上表示有理数的方法，理解“在数轴上左边的点表示的数小于右边点表示的数”是解决问题的关键．
21．（8分）化简：
（1）2m3﹣（+2m2）﹣（﹣3m2）+3m3+m；
（2）（3x2﹣4xy）﹣2（﹣2xy+y2）．
【分析】（1）将原式统一成加法后合并同类项即可；
（2）将原式去括号后合并同类项即可．
【解答】解：（1）原式＝2m3﹣2m2+3m2+3m3+m
＝5m3+m2+m；
（2）原式＝3x2﹣4xy+4xy﹣2y2
＝3x2﹣2y2．
【点评】本题考查整式的加减，熟练掌握相关运算法则是解题的关键．
22．（5分）先化简，后求值：3ab2﹣（ab+2ab2）+4ab，其中|a﹣1|+（b+2）2＝0．
【分析】先根据整式的加减运算法则化简，然后根据非负数的性质求出a、b的值，最后代入计算即可．
【解答】解：3ab2﹣（ab+2ab2）+4ab
＝3ab2﹣ab﹣2ab2+4ab
＝ab2+3ab，
∵|a﹣1|+（b+2）2＝0，
又∵|a﹣1|≥0，（b+2）2≥0，
∴a﹣1＝0，b+2＝0，
∴a＝1，b＝﹣2，
∴原式＝1×（﹣2）2+3×1×（﹣2）
＝1×4+（﹣6）
＝4+（﹣6）
＝﹣2．
【点评】本题考查了整式的加减﹣化简求值，非负数的性质，熟练掌握整式的加减运算法则是解题的关键．
23．（5分）已知a、b互为相反数，c、d互为倒数，|m|＝1，求﹣2cd+m2的值．
【分析】根据相反数的性质及倒数的定义可得a+b＝0，cd＝1，再由|m|＝1可得m2＝1，然后将其代入﹣2cd+m2中计算即可．
【解答】解：∵a、b互为相反数，c、d互为倒数，|m|＝1，
∴a+b＝0，cd＝1，m2＝1，
∴﹣2cd+m2
＝0﹣2+1
＝﹣1．
【点评】本题考查有理数的运算，结合已知条件求得a+b＝0，cd＝1，m2＝1是解题的关键．
24．（8分）水果超市最近新进了一批橙子，每斤进价10元，9月29日每斤售价15元，国庆黄金周9月30日起试行机动价格，价格超出前一天的部分记为正，不足前一天的部分记为负，超市记录了国庆黄金周橙子的售价变化情况和售出情况：
（1）10月4日超市售出的橙子的单价是多少元？
（2）10月4日超市售出的橙子的收益如何？（盈利或亏损的钱数）
（3）国庆黄金周水果超市出售此种橙子的收益如何？
【分析】（1）根据正数和负数的实际意义列式计算即可；
（2）结合（1）中所求列式计算即可；
（3）根据正数和负数的实际意义列式计算即可．
【解答】解：（1）15﹣1﹣3+2﹣1﹣3＝9（元），
即10月4日超市售出的橙子的单价是9元；
（2）（9﹣10）×10＝﹣10（元），
即10月4日超市售出的橙子的收益为亏损10元；
（3）9月30日的利润为（15﹣1﹣10）×15＝60（元）；
10月1日的利润为（15﹣1﹣3﹣10）×30＝30（元）；
10月2日的利润为（15﹣1﹣3+2﹣10）×10＝30（元）；
10月3日的利润为（15﹣1﹣3+2﹣1﹣10）×35＝70（元）；
10月4日的利润为（15﹣1﹣3+2﹣1﹣3﹣10）×10＝﹣10（元）；
10月5日的利润为（15﹣1﹣3+2﹣1﹣3+4﹣10）×5＝15（元）；
10月6日的利润为（15﹣1﹣3+2﹣1﹣3+4﹣8﹣10）×40＝﹣200（元）；
则60+30+30+70﹣10+15﹣200＝﹣5（元），
即国庆黄金周水果超市出售此种橙子的收益为亏损5元．
【点评】本题考查正数和负数及有理数运算的实际应用，结合已知条件列得正确的算式是解题的关键．
25．（8分）相较于自己做一顿饭较高的时间成本，点外卖不仅可以节省大量的时间，也可以满足年轻人对于“吃”的需求．某餐厅打算在美团和饿了么平台根据点餐金额采用不同的优感惠策略，在美团平台实施方案如下：
在饿了么平台实施方案如下：
（1）若小华点餐金额为60元，那么在美团和饿了么平台上的实际付款金额分别是多少？
（2）若小华点餐金额为n元（n＞158），那么小华在美团和饿了么平台上的实际付款金额分别是多少？（用含n的代数式表示）
（3）若小华在两个平台各点单一次，两次点餐金额共300元．其中美团点餐金额比饿了么点餐金额低，设美团的点餐金额是x元，求两次实际付款金额共多少？（用含x的代数式表示）
【分析】（1）根据优惠方案列式计算即可；
（2）由n＞158和优惠方案可得在美团平台上的实际付款金额为（n﹣30）元；分158＜n≤200和n＞200两种情况列代数式表示在饿了么平台上的实际付款金额即可；
（3）分三种情况求出两次实际付款金额．
【解答】解：（1）小华点餐金额为60元，那么在美团平台上的实际付款金额为60﹣10＝50（元）；
在饿了么平台上的实际付款金额为40+（60﹣40）×0.9＝58（元）；
（2）小华点餐金额为n元（n＞158），那么在美团平台上的实际付款金额为（n﹣30）元；
当158＜n≤200时，在饿了么平台上的实际付款金额为40+0.9（n﹣40）＝（0.9n+4）元，
当n＞200时，在饿了么平台上的实际付款金额为40+0.9×（200﹣40）+0.8（n﹣200）＝（0.8n+24）元，
（3）当0＜x≤55时，300﹣x≥200，此时两次实际付款金额共x+40+0.9×（200﹣40）+0.8（300﹣x﹣200）＝（0.2x+264）元；
当55＜x≤100时，300﹣x＞200，此时两次实际付款金额共x﹣10+40+0.9×（200﹣40）+0.8（300﹣x﹣200）＝（0.2x+254）元；
当100＜x＜150时，300﹣x＜200，此时两次实际付款金额共x﹣10+40+0.9（300﹣x﹣40）＝（0.1x+264）元．
【点评】本题考查列代数式，解题的关键是读懂题意，能分类列出代数式．
26．（10分）小明在一条长方形的纸带上画了一条数轴，进行操作井研究．
（1）操作1：折叠纸带，使数轴上表示1的点与表示﹣1的点重合，则表示数﹣2的点与表示数 2 的点重合．
（2）操作2：折叠纸带，使数轴上表示1的点与表示﹣5的点重合，则表示数a的点与表示数 ﹣4﹣a 的点重合．
（3）操作3：如图，在数轴上剪下6个单位长度（从﹣1到5）的一条线段，并把这条线段沿某点向左对折，然后在重叠部分的某处剪一刀得到三条线段，若这三条线段的长度之比为1：2：2，则折痕处对应的点表示的数可能是几？
【分析】折叠纸带，折痕处的点到重合的两点的距离相等．找到折痕处的点表示的数是解题的关键．数轴上两点的距离是两点表示的两数差的绝对值．第三问要分类讨论．
【解答】解：（1）折叠纸带，使数轴上表示1的点与表示﹣1的点重合，
折痕处的点表示的数为0．
则表示数﹣2的点与表示数2的点重合．
故答案为：2．
（2）折叠纸带，使数轴上表示1的点与表示﹣5的点重合，
折痕处的点表示的数为﹣2，
设与表示数a的点重合的点表示的数是x，
﹣2﹣a＝x﹣（﹣2），
x＝﹣4﹣a．
故答案为：﹣4﹣a．
（3）设表示﹣1的点是A，表示5的是D，
∴AD＝6．
①当AB：BC：CD＝1：2：2时，
设AB＝a，BC＝2a，CD＝2a，
a+2a+2a＝6，
解得a＝1.2，
∴AB＝1.2，BC＝2.4，CD＝2.4，
∴折痕处对应的点所表示的数是：﹣1+1.2+1.2＝1.4，
②当AB：BC：CD＝2：1：2时，
设AB＝2a，BC＝a，CD＝2a，
2a+a+2a＝6，
解得 a＝1.2，
∴．AB＝2.4，BC＝1.2，CD＝2.4，
∴折痕处对应的点所表示的数是：﹣1+2.4+0.6＝2．
③当AB：BC：CD＝2：2：1时，
设AB＝2a，BC＝2a，CD＝a，
2a+2a+a＝6，
解得a＝1.2，
∴AB＝2.4，BC＝2.4，CD＝1.2，
∴折痕处对应的点所表示的数是：﹣1+2.4+1.2＝2.6，
综上所述：折痕处对应的点所表示的数可能是1.4或2或2.6．
【点评】考查了实数和数轴的关系，及数轴上的折叠变换问题，明确①数轴上折叠后，折痕处的点到重合的两点的距离相等．②数轴上两点的距离是两点表示的两数差的绝对值．
附加题（本题10分）
27．（﹣1）2＝ 1 .（﹣1）3＝ ﹣1 ．
【分析】负数的偶数次方为正数，负数的奇数次方为负数，据此计算即可．
【解答】解：（﹣1）2＝1，（﹣1）3＝﹣1．
故答案为：1，﹣1．
【点评】本题考查有理数的乘方，掌握“负数的偶数次方为正数，负数的奇数次方为负数”是本题的关键．
28．计算（﹣1）n．
【分析】根据“负数的偶数次方为正数，负数的奇数次方为负数”计算即可．
【解答】解：当n为偶数时，（﹣1）n＝1；
当n为奇数时，（﹣1）n＝﹣1．
【点评】本题考查有理数的乘方，熟练掌握“负数的偶数次方为正数，负数的奇数次方为负数”是解答本题的关键．
29．桌子上有7只杯口朝上的茶杯，每次翻转2只，能否经过若干次翻转使7只杯口全部朝下？若用“+1”、“﹣1”分别表示“朝上”、“朝下”，请用有理数的运算说明理由．
【分析】根据有理数的乘法运算，同号得正，同时改变四个杯子的开口方向，乘积符号不变．
【解答】解：把茶杯口朝上的状态记为+1，口朝下的状态记为﹣1．
根据题意，开始时7个茶杯的状态都是+1，它们的乘积也为+1，
每次操作翻转2只茶杯，相当于把7个数中的2个改变符号，但把一个乘积的偶数个因数改变符号时，并不能改变乘积的符号．
因此，不管你进行多少次操作都不能使乘积变为﹣1．
当7只茶杯都口朝下时，所有的状态都是﹣1，它们的积是﹣1，
所以不可能通过操作把7只茶杯都变得口朝下．
【点评】此题考查了奇数与偶数，以及学生动手操作的能力，在翻动时，注意按一定规律进行．
30．桌子上有23只杯口朝上的茶杯，每次翻转3只，经过20次翻转 不能 使23只杯口全部朝下．（填“能”或“不能”）
【分析】假设经过20次翻转能使23只杯口全部朝下，设有n只杯子经过3次翻转，则有（23﹣n）只杯子经过1次翻转，根据共翻转3×20次，可列出关于n的一元一次方程，解之可求出n的值，由该值不为整数，可得出假设不成立，即经过20次翻转不能使23只杯口全部朝下．
【解答】解：不能，理由如下：
假设经过20次翻转能使23只杯口全部朝下，
∵杯口朝上的茶杯经过奇数次翻转杯口朝下，
∴设有n只杯子经过3次翻转，则有（23﹣n）只杯子经过1次翻转，
根据题意得：3n+（23﹣n）＝3×20，
整理得：2n＝37，
解得：n＝，这与n为正整数相矛盾，
∴假设不成立，即经过20次翻转不能使23只杯口全部朝下．
（若出现5，7，9，…次翻转的，同样整理后方程左边为偶数，右边为奇数）
故答案为：不能．
【点评】本题考查了奇数与偶数以及解一元一次方程，根据翻转的规律，列出一元一次方程是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/10/14 9:06:56；用户：492175055；邮箱：492175055@qq.cm；学号：5783273日期
9月30日
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
售价变化（元）
﹣1
﹣3
+2
﹣1
﹣3
+4
﹣8
售出斤数
15
30
10
35
10
5
40
美团平台一次性点餐金额
优惠措施
不超过55元
无优惠
超过55元，但不超过158元
减10元
超过158元
减30元
饿了么平台一次性点餐金额
优惠措施
不超过40元的部分
无优惠
超过40元，但不超过200元的部分
打9折
超过200元的部分
打8折
日期
9月30日
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
售价变化（元）
﹣1
﹣3
+2
﹣1
﹣3
+4
﹣8
售出斤数
15
30
10
35
10
5
40
美团平台一次性点餐金额
优惠措施
不超过55元
无优惠
超过55元，但不超过158元
减10元
超过158元
减30元
饿了么平台一次性点餐金额
优惠措施
不超过40元的部分
无优惠
超过40元，但不超过200元的部分
打9折
超过200元的部分
打8折