江苏省无锡市惠山区锡山高级中学实验学校2023-2024学年七年级上学期期中数学试卷

这是一份江苏省无锡市惠山区锡山高级中学实验学校2023-2024学年七年级上学期期中数学试卷，共13页。试卷主要包含了填空题，认真解一解等内容，欢迎下载使用。
1．（3分）3的相反数是（ ）
A．﹣3B．﹣C．3D．
2．（3分）昆明市某天的最高气温为12℃，最低气温为﹣2℃，这天的最高气温比最低气温高（ ）
A．﹣10℃B．10℃C．14℃D．﹣14℃
3．（3分）下列各数中负数是（ ）
A．﹣（﹣2）B．﹣|﹣2|C．（﹣2）2D．﹣（﹣2）3
4．（3分）在代数式：，0，﹣5，，，2s2中，单项式有（ ）
A．3B．4C．5D．6
5．（3分）下列计算正确的是（ ）
A．6a﹣5a＝1B．a+2a2＝3a
C．﹣（a﹣b）＝﹣a+bD．2（a+b）＝2a+b
6．（3分）下列说法正确的是（ ）
A．32ab3的次数是6次 B．πx的系数为1，次数为2
C．﹣3x2y+4x﹣1的常数项是﹣1 D．多项式2x2+xy+3是四次三项式
7．（3分）用代数式表示图中阴影部分面积正确的是（ ）
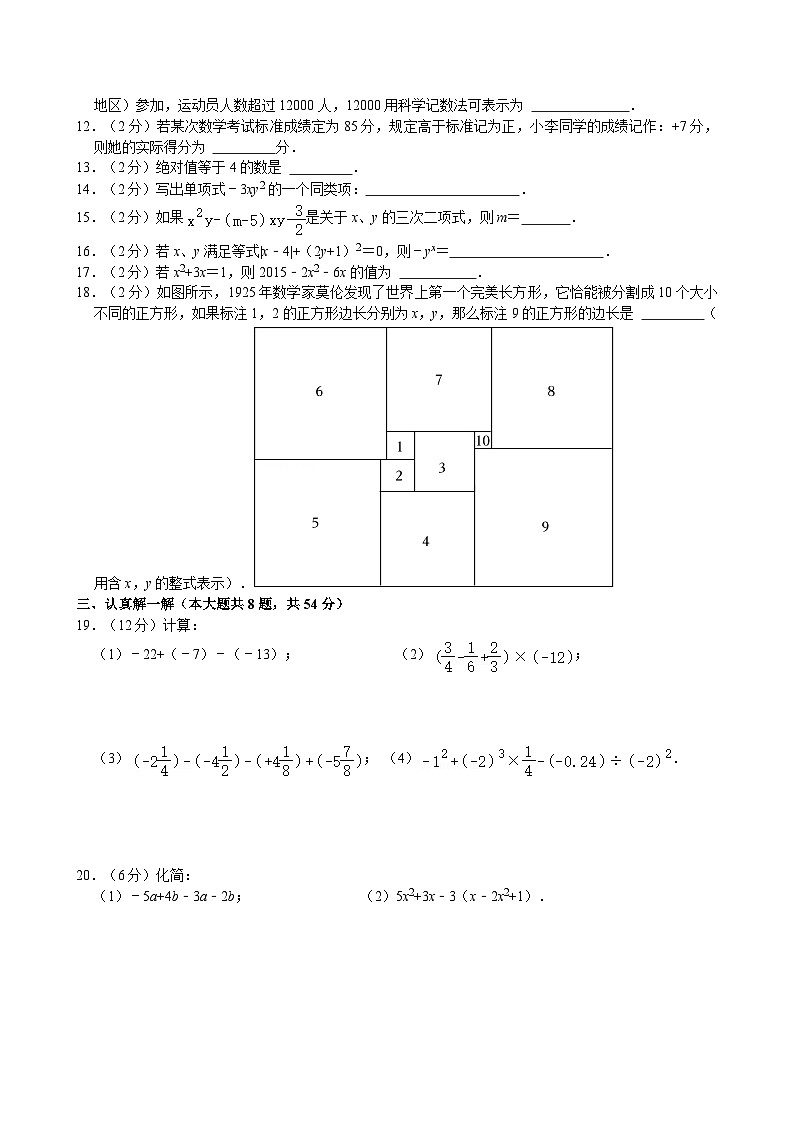
A．B．
C．D．
8．（3分）一个长方形的周长为8a+10b，若一边长为a+2b，则它的另一边长为（ ）
A．3a+3bB．2a+4bC．7a+8bD．2a+3b
9．（3分）
如图a，b在数轴上的位置如图所示．化简：|a﹣c|﹣|a+b|﹣|c﹣b|结果是（ ）
A．0B．﹣2aC．2bD．2c
10．（3分）一只小虫在数轴上从A点出发，第1次向正方向爬行1个单位后，第2次向负方向爬行2个单位，第3次又向正方向爬行3个单位……按上述规律，它第2023次刚好爬到数轴上的原点处，小虫爬行过程中经过数轴上﹣50这个数的次数是（ ）
A．99B．100C．101D．102
二、填空题（本大题共8小题，每空2分，共16分.不需写出解答过程，只需把答案直接填写在答题卷上相应的位置）
11．（2分）杭州第19届亚运会是中国第三次举办亚洲最高规格的国际综合性体育赛事．共有45个国家（地区）参加，运动员人数超过12000人，12000用科学记数法可表示为 ．
12．（2分）若某次数学考试标准成绩定为85分，规定高于标准记为正，小李同学的成绩记作：+7分，则她的实际得分为 分．
13．（2分）绝对值等于4的数是 ．
14．（2分）写出单项式﹣3xy2的一个同类项： ．
15．（2分）如果是关于x、y的三次二项式，则m＝ ．
16．（2分）若x、y满足等式|x﹣4|+（2y+1）2＝0，则﹣yx＝ ．
17．（2分）若x2+3x＝1，则2015﹣2x2﹣6x的值为 ．
18．（2分）如图所示，1925年数学家莫伦发现了世界上第一个完美长方形，它恰能被分割成10个大小不同的正方形，如果标注1，2的正方形边长分别为x，y，那么标注9的正方形的边长是 （用含x，y的整式表示）．
三、认真解一解（本大题共8题，共54分）
19．（12分）计算：
（1）﹣22+（﹣7）﹣（﹣13）； （2）；
（3）； （4）．
20．（6分）化简：
（1）﹣5a+4b﹣3a﹣2b； （2）5x2+3x﹣3（x﹣2x2+1）．
21．（4分）先化简，再求值：已知A＝5a2﹣6ab，且B＝﹣4a2+3ab+5，求A﹣2B的值．其中a＝﹣1，．
22．（4分）数学活动课上，老师和同学们玩游戏．老师说：“你们任意想一个数，把这个数除以7后加1，然后乘以28，再减去你们原来所想的那个数的4倍，我可以猜出你们计算的结果．”同学们不相信，接连试了几个数，发现老师都正确．你能说说其中的理由吗？
23．（6分）张先生到某大楼办事，假定乘电梯向上一楼记为+1，向下一楼记为﹣1．王先生从1楼出发，电梯上下楼层依次记录如下（单位：层）：+5，﹣6，+7，﹣7，+19，﹣8，﹣10．
（1）请你通过计算说明王先生最后是否回到出发点1楼？
（2）该大楼每层高3.2米，电梯每上或下1米需要耗电0.1度．根据王先生现在所处的位置，你算一算，当他办事时电梯需要耗电多少度？
24．（6分）如图是一块长方形花园，内部修有两个凉亭及过道，其余部分种植花圃（阴影部分）．
（1）用整式表示花圃的面积；
（2）若a＝2米，修建花圃的成本是每平方米80元，求修建花圃所需费用．
25．（8分）某商店出售羽毛球拍和羽毛球，羽毛球拍每副定价1500元，羽毛球每桶定价100元，促销期间有两种付费方式：A．买一副羽毛球赠送2桶羽毛球
B．羽毛球拍和羽毛球都按定价的9折优惠
（1）某训练队购买6副羽毛球拍和羽毛球x（x＞12）桶，请你帮他计算两种付费金额（结果需化简）．
（2）当x＝35时，通过计算说明哪种付费方式更划算？
26．（8分）如图，数轴上从左到右依次有A、B、C、D四个点，A、B之间的距离为a+b，B、C之间的距离为2a﹣b，B、D之间的距离为5a+2b，将直径为1的圆形纸片按如图所示的方式放置在点A处，并沿数轴水平方向向右滚动．
（1）若圆形纸片从点A处滚到点C处，恰好滚动了n（n为正整数）圈，则a＝ （用含n的代数式表示），a是 （填“有理数”或“无理数”）；
（2）若圆形纸片从点A处滚动1圈后，恰好到达点B处，求C、D之间的距离（结果保留π）；
（3）若点A表示的数为π，圆形纸片从点A处滚动到点B、C、D处的圈数均为整数，其中圆形纸片从点A处滚动3圈后，恰好到达点C处，求点D表示的数．
2023-2024学年江苏省无锡市惠山区锡山高级中学实验学校七年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分.在每小题所给出的四个选项中，
1．（3分）3的相反数是（ ）
A．﹣3B．﹣C．3D．
【分析】根据相反数的性质，互为相反数的两个数和为0，采用逐一检验法求解即可．
【解答】解：根据概念，3的相反数在3的前面加﹣，则3的相反数是﹣3．
故选：A．
【点评】本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“﹣”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．
2．（3分）昆明市某天的最高气温为12℃，最低气温为﹣2℃，这天的最高气温比最低气温高（ ）
A．﹣10℃B．10℃C．14℃D．﹣14℃
【分析】用最高气温减去最低气温即可，有理数减法法则：减去一个数，等于加上这个数的相反数．
【解答】解：12﹣（﹣2）＝12+2＝14（℃），
即这天的最高气温比最低气温高14℃．
故选：C．
【点评】本题主要考查了有理数的减法，熟记有理数的减法法则是解答本题的关键．
3．（3分）下列各数中负数是（ ）
A．﹣（﹣2）B．﹣|﹣2|C．（﹣2）2D．﹣（﹣2）3
【分析】根据有理数的乘方的性质，相反数的定义，绝对值的意义依次进行化简即可得出答案．
【解答】解：A、﹣（﹣2）＝2是正数，
B、﹣|﹣2|＝﹣2，是负数，
C、（﹣2）2＝4是正数，
D、﹣（﹣2）3＝8是正数，
故选：B．
【点评】本题主要考查了有理数的乘方的性质，相反数的定义，绝对值的意义，难度适中．
4．（3分）在代数式：，0，﹣5，，，2s2中，单项式有（ ）
A．3B．4C．5D．6
【分析】根据单项式的意义，即可解答．
【解答】解：在代数式：，0，﹣5，，，2s2中，单项式有，0，﹣5，2s2，共有4个，
故选：B．
【点评】本题考查了单项式，熟练掌握单项式的意义是解题的关键．
5．（3分）下列计算正确的是（ ）
A．6a﹣5a＝1B．a+2a2＝3a
C．﹣（a﹣b）＝﹣a+bD．2（a+b）＝2a+b
【分析】根据去括号法则和合并同类项法则计算即可求解．
【解答】解：A．6a﹣5a＝a，即A项不合题意，
B．a和2a2不是同类项不能合并，即B项不合题意，
C．﹣（a﹣b）＝﹣a+b，即C项符合题意，
D．2（a+b）＝2a+2b，即D项不合题意，
故选：C．
【点评】本题考查了整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
6．（3分）下列说法正确的是（ ）
A．32ab3的次数是6次
B．πx的系数为1，次数为2
C．﹣3x2y+4x﹣1的常数项是﹣1
D．多项式2x2+xy+3是四次三项式
【分析】根据单项式、多项式的概念及单项式的次数、系数的定义解答．
【解答】解：A、32ab3的次数是4次，故选项错误；
B、πx的系数为π，次数为1，故选项错误；
C、﹣3x2y+4x﹣1的常数项是﹣1，故选项正确；
D、多项式2x2+xy+3是二次三项式，故选项错误．
故选：C．
【点评】考查了单项式、多项式，需注意：单项式中的数字因数叫做这个单项式的系数，几个单项式的和叫做多项式，单项式中，所有字母的指数和叫做这个单项式的次数．
7．（3分）用代数式表示图中阴影部分面积正确的是（ ）
A．B．
C．D．
【分析】用长方形的面积减去2个圆的面积即可．
【解答】解：阴影部分的面积为ab﹣2×πb2＝ab﹣πb2，
故选：C．
【点评】本题主要考查列代数式，解题的关键是根据图形找到阴影部分的面积＝长方形的面积减去2个圆的面积．
8．（3分）一个长方形的周长为8a+10b，若一边长为a+2b，则它的另一边长为（ ）
A．3a+3bB．2a+4bC．7a+8bD．2a+3b
【分析】根据题意列出算式（8a+10b）﹣（a+2b），再去括号、合并同类项即可．
【解答】解：它的另一边长为（8a+10b）﹣（a+2b）
＝4a+5b﹣a﹣2b
＝3a+3b，
故选：A．
【点评】本题主要考查整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
9．（3分）
如图a，b在数轴上的位置如图所示．化简：|a﹣c|﹣|a+b|﹣|c﹣b|结果是（ ）
A．0B．﹣2aC．2bD．2c
【分析】根据数轴判断a、b、c、0的关系，对|a﹣c|﹣|a+b|﹣|c﹣b|化简求结果．
【解答】解：观察数轴可得，a＜b＜0＜c，|a|＞|c|，
|a﹣c|﹣|a+b|﹣|c﹣b|＝c﹣a﹣（﹣a﹣b）﹣（c﹣b）＝2b，
故选：C．
【点评】本题考查了数轴和绝对值，关键是根据数轴去绝对值．
10．（3分）一只小虫在数轴上从A点出发，第1次向正方向爬行1个单位后，第2次向负方向爬行2个单位，第3次又向正方向爬行3个单位……按上述规律，它第2023次刚好爬到数轴上的原点处，小虫爬行过程中经过数轴上﹣50这个数的次数是（ ）
A．99B．100C．101D．102
【分析】先根据题意求出点A所表示的数，再求出小虫第一次经过﹣50时的爬行次数，据此可解决问题．
【解答】解：由题知，
令点A所表示的数为a，
则第1次爬行后的点所表示的数为a+1，
第2次爬行后的点所表示的数为a+1﹣2＝a﹣1，
第3次爬行后的点所表示的数为a﹣1+3＝a+2，
第4次爬行后的点所表示的数为a+2﹣4＝a﹣2，
…，
所以第2n次爬行后的点所表示的数为a﹣n，
故第2022次爬行后的点所表示的数为a﹣1011，
则第2023次爬行后的点所表示的数为a﹣1011+2023＝a+1012．
又因为第2023次刚好爬到数轴上的原点处，
所以a+1012＝0，
则a＝﹣1012，
即点A所表示的数为﹣1012．
又因为﹣50﹣（﹣1012）＝962，
所以表示﹣50的点在A点的右边，与A点相距962个单位长度．
又因为第1次爬行后的点在点A的右边1个单位长度处，
第3次爬行后的点在点A的右边2个单位长度处，
第5次爬行后的点在点A的右边3个单位长度处，
…，
所以第（2n﹣1）次爬行后的点在点A的右边n个单位长度处，
且2×962﹣1＝1923，
即小虫爬行第1923次时，对应点所表示的数为﹣50，
所以从第1923次开始（包括第1923次），后面的每次爬行都经过﹣50这个数．
又因为2023﹣1923+1＝101，
所以小虫爬行过程中经过数轴上﹣50这个数的次数是101．
故选：C．
【点评】本题考查数字变化的规律，能根据题意求出点A所表示的数及小虫第一次经过﹣50时的爬行次数是解题的关键．
二、填空题（本大题共8小题，每空2分，共16分.不需写出解答过程，只需把答案直接填写在答题卷上相应的位置）
11．（2分）杭州第19届亚运会是中国第三次举办亚洲最高规格的国际综合性体育赛事．共有45个国家（地区）参加，运动员人数超过12000人，12000用科学记数法可表示为 1.2×104 ．
【分析】科学记数法的表现形式为a×10n的形式，其中1≤|a|＜10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正整数，当原数绝对值小于1时，n是负整数．
【解答】解：12000＝1.2×104，
故答案为：1.2×104．
【点评】本题考查了科学记数法的表示方法，科学记数法的表现形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键是要正确确定a的值以及n的值．
12．（2分）若某次数学考试标准成绩定为85分，规定高于标准记为正，小李同学的成绩记作：+7分，则她的实际得分为 92 分．
【分析】根据题意可得：她的实际得分＝85+7，然后进行计算即可解答．
【解答】解：由题意得：85+7＝92（分），
∴她的实际得分为92分，
故答案为：92．
【点评】本题考查了正数和负数，熟练掌握正数和负数的意义是解题的关键．
13．（2分）绝对值等于4的数是 ±4 ．
【分析】利用绝对值的代数意义判断即可得到结果．
【解答】解：绝对值等于4的数是±4．
故答案为：±4．
【点评】此题考查了绝对值，熟练掌握绝对值的代数意义是解本题的关键．
14．（2分）写出单项式﹣3xy2的一个同类项： xy2（答案不唯一：形如Zxy2，Z≠0且Z为常数） ．
【分析】直接利用同类项的定义分析得出答案．
【解答】解：单项式xy2的一个同类项可以为：xy2（答案不唯一：形如Zxy2，Z≠0且Z为常数）．
故答案为：xy2（答案不唯一：形如Zxy2，Z≠0且Z为常数）．
【点评】此题主要考查了同类项，正确把握同类项的定义是解题关键．
15．（2分）如果是关于x、y的三次二项式，则m＝ 5 ．
【分析】根据多项式的意义可得：﹣（m﹣5）＝0，然后进行计算即可解答．
【解答】解：∵是关于x、y的三次二项式，
∴﹣（m﹣5）＝0，
解得：m＝5，
故答案为：5．
【点评】本题考查了多项式，熟练掌握多项式的意义是解题的关键．
16．（2分）若x、y满足等式|x﹣4|+（2y+1）2＝0，则﹣yx＝ ﹣ ．
【分析】根据非负数的性质列式求出x、y的值，然后代入代数式进行计算即可得解．
【解答】解：∵|x﹣4|+（2y+1）2＝0，
∴x﹣4＝0，2y+1＝0，
解得x＝4，y＝﹣，
∴﹣yx＝﹣（﹣）4＝﹣．
故答案为：﹣．
【点评】本题主要考查的是非负数的性质，即几个非负数的和为0时，这几个非负数都为0．
17．（2分）若x2+3x＝1，则2015﹣2x2﹣6x的值为 2013 ．
【分析】把代数式2015﹣2x2﹣6x变形为2015﹣2（x2+3x），然后整体代入求值即可．
【解答】解：∵x2+3x＝1，
∴2015﹣2x2﹣6x
＝2015﹣2（x2+3x）
＝2015﹣2×1
＝2015﹣2
＝2013，
故答案为：2013．
【点评】本题考查了代数式求值，熟练掌握整体代入思想求值是解题的关键．
18．（2分）如图所示，1925年数学家莫伦发现了世界上第一个完美长方形，它恰能被分割成10个大小不同的正方形，如果标注1，2的正方形边长分别为x，y，那么标注9的正方形的边长是 5x （用含x，y的整式表示）．
【分析】已知标注1，2的正方形边长分别为x，y，先分析得到前5个正方形的边长，再由标注6的正方形的边长等于标注5的正方形的边长加上标注2的正方形的边长再减去标注1的正方形的边长，得到标注6的正方形的边长；标注7的正方形的边长等于标注6的正方形的边长减去标注1的正方形的边长，也等于标注1，3，10的正方形的边长之和，据此不难得到标注10的正方形的边长，再根据3的边长+4的边长﹣10的边长即可得出答案．
【解答】解：因为标注1，2的正方形边长为x、y，
所以标注为3的正方形边长为x+y，
则4的边长等于y+（x+y）＝x+2y，
5的边长等于y+（x+2y）＝x+3y，
6的边长等于y﹣x+（x+3y）＝4y，
10的边长等于（4y﹣x）﹣x﹣（x+y）＝3y﹣3x．
所以标注9的正方形的边长为x+y+x+2y﹣（3y﹣3x）＝5x，
故答案为：5x．
【点评】本题考查列代数式，正确找出规律是解题关键．
三、认真解一解（本大题共8题，共54分）
19．（12分）计算：
（1）﹣22+（﹣7）﹣（﹣13）；
（2）；
（3）；
（4）．
【分析】（1）按照从左到右的顺序进行计算，即可解答；
（2）利用乘法分配律进行计算，即可解答；
（3）利用加法交换律和结合律进行计算，即可解答；
（4）先算乘方，再算乘除，后算加减，即可解答．
【解答】解：（1）﹣22+（﹣7）﹣（﹣13）
＝﹣29+13
＝﹣16；
（2）
＝﹣12×+12×﹣12×
＝﹣9+2﹣8
＝﹣7﹣8
＝﹣15；
（3）
＝﹣2+4﹣4﹣5
＝（﹣2+4）+（﹣4﹣5）
＝2+（﹣10）
＝﹣7；
（4）
＝﹣1+（﹣8）×﹣（﹣0.24）÷4
＝﹣1+（﹣2）+0.06
＝﹣3+0.06
＝﹣2.94．
【点评】本题考查了有理数的混合运算，准确熟练地进行计算是解题的关键．
20．（6分）化简：
（1）﹣5a+4b﹣3a﹣2b；
（2）5x2+3x﹣3（x﹣2x2+1）．
【分析】（1）直接合并同类项即可；
（2）先去括号，再合并同类项即可．
【解答】解：（1）原式＝﹣8a+2b；
（2）原式＝5x2+3x﹣3x+6x2﹣3
＝11x2﹣3．
【点评】本题主要考查整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
21．（4分）先化简，再求值：已知A＝5a2﹣6ab，且B＝﹣4a2+3ab+5，求A﹣2B的值．其中a＝﹣1，．
【分析】此题需要先去括号，再合并同类项，将原整式化简，然后再将a，b的值代入求解即可．
【解答】解：∵A＝5a2﹣6ab，B＝﹣4a2+3ab+5，
∴A﹣2B＝（5a2﹣6ab）﹣2（﹣4a2+3ab+5）
＝5a2﹣6ab+8a2﹣6ab﹣10
＝13a2﹣12ab﹣10，
当a＝﹣1，b＝﹣时，
原式＝13×（﹣1）2﹣12×（﹣1）×（﹣）﹣10
＝13﹣6﹣10
＝﹣3．
【点评】此题考查了整式的混合运算，主要考查了整式的加减法、去括号、合并同类项的知识点．注意运算顺序以及符号的处理．
22．（4分）数学活动课上，老师和同学们玩游戏．老师说：“你们任意想一个数，把这个数除以7后加1，然后乘以28，再减去你们原来所想的那个数的4倍，我可以猜出你们计算的结果．”同学们不相信，接连试了几个数，发现老师都正确．你能说说其中的理由吗？
【分析】设原来的数为x，则计算的结果为（+1）×28﹣4x，进一步计算即可．
【解答】解：设原来的数为x，
则计算的结果为（+1）×28﹣4x
＝4x+28﹣4x
＝28，
∴不论原来的数是多少，最后的结果都是28．
【点评】本题主要考查有理数和整式的混合运算，解题的关键是表示出原来的数及运算的结果．
23．（6分）张先生到某大楼办事，假定乘电梯向上一楼记为+1，向下一楼记为﹣1．王先生从1楼出发，电梯上下楼层依次记录如下（单位：层）：+5，﹣6，+7，﹣7，+19，﹣8，﹣10．
（1）请你通过计算说明王先生最后是否回到出发点1楼？
（2）该大楼每层高3.2米，电梯每上或下1米需要耗电0.1度．根据王先生现在所处的位置，你算一算，当他办事时电梯需要耗电多少度？
【分析】（1）把这些正数和负数全部相加，进行计算即可解答；
（2）把这些正数和负数的绝对值全部相加，进行计算即可解答；
【解答】解：（1）由题意得：+5+（﹣6）+（+7）+（﹣7）+（+19）+（﹣8）+（﹣10）＝0，
∴王先生最后回到出发点1楼；
（2）|+5|+|﹣6|+|+7|+|﹣7|+|+19|+|﹣8|+|﹣10|
＝5+6+7+7+19+8+10
＝62（层），
∴62×3.2×0.1＝19.84（度），
∴当他办事时电梯需要耗电19.84度．
【点评】本题考查了有理数的混合运算，正数和负数，准确熟练地进行计算是解题的关键．
24．（6分）如图是一块长方形花园，内部修有两个凉亭及过道，其余部分种植花圃（阴影部分）．
（1）用整式表示花圃的面积；
（2）若a＝2米，修建花圃的成本是每平方米80元，求修建花圃所需费用．
【分析】（1）根据大矩形面积减去两个小矩形面积表示出花圃面积即可；
（2）把a的值代入计算即可求出所求．
【解答】解：（1）根据题意得：（7.5+12.5）×（a+2a+2a+2a+a）﹣12.5•2a×2
＝20•8a﹣50a
＝160a﹣50a
＝110a（m2）；
（2）当a＝2时，花圃面积为110×2＝220（m2），
修建花圃所需费用：220×80＝17600（元）．
【点评】此题考查了代数式求值，以及列代数式，根据题意列出关系式是解本题的关键．
25．（8分）某商店出售羽毛球拍和羽毛球，羽毛球拍每副定价1500元，羽毛球每桶定价100元，促销期间有两种付费方式：A．买一副羽毛球赠送2桶羽毛球
B．羽毛球拍和羽毛球都按定价的9折优惠
（1）某训练队购买6副羽毛球拍和羽毛球x（x＞12）桶，请你帮他计算两种付费金额（结果需化简）．
（2）当x＝35时，通过计算说明哪种付费方式更划算？
【分析】（1）根据题意列得代数式即可；
（2）将x＝35分别代入（1）中所列代数式运算后比较大小即可．
【解答】解：（1）A方式：1500×6+100（x﹣12）＝（100x+7800）元；
B方式：1500×0.9×6+100×0.9x＝（90x+8100）元；
（2）当x＝35时，
100x+7800＝3500+7800＝11300，90x+8100＝3150+8100＝11250，
∵11300＞11250，
∴B种付费方式更划算．
【点评】本题考查列代数式及代数式求值，结合已知条件列得正确的代数式是解题的关键．
26．（8分）如图，数轴上从左到右依次有A、B、C、D四个点，A、B之间的距离为a+b，B、C之间的距离为2a﹣b，B、D之间的距离为5a+2b，将直径为1的圆形纸片按如图所示的方式放置在点A处，并沿数轴水平方向向右滚动．
（1）若圆形纸片从点A处滚到点C处，恰好滚动了n（n为正整数）圈，则a＝ （用含n的代数式表示），a是 无理数 （填“有理数”或“无理数”）；
（2）若圆形纸片从点A处滚动1圈后，恰好到达点B处，求C、D之间的距离（结果保留π）；
（3）若点A表示的数为π，圆形纸片从点A处滚动到点B、C、D处的圈数均为整数，其中圆形纸片从点A处滚动3圈后，恰好到达点C处，求点D表示的数．
【分析】（1）表示圆的周长，再根据滚动的圈数得出滚动的距离即可得出答案；
（2）圆形纸片从点A处滚动1圈到达点B处，可得a+b＝π，再得出CD＝3a+3b，整体代入即可；
（3）根据“圆形纸片从点A处滚动到点B、C、D处的圈数均为整数，且从点A处滚动到点C滚动3圈”，因此分两种情况进行解答，即AB为1圈，BC为2圈，或AB为2圈，BC为1圈．
【解答】解：（1）圆形纸片的直径为1，因此周长为π，滚动n圈的距离为nπ，
而AC＝（a+b）+（2a﹣b）＝3a，
所以3a＝nπ，
即a＝，是无理数，
故答案为：，无理数；
（2）圆形纸片从点A处滚动1圈到达点B处，所以有a+b＝π，
所以CD＝（5a+2b）﹣（2a﹣b）＝3a+3b＝3（a+b）＝3π，
答：C、D之间的距离为3π；
（3）由（2）得，CD＝3AB，
由于圆形纸片从点A处滚动到点B、C、D处的圈数均为整数，且从点A处滚动到点C滚动3圈，
因此有①当A、B的距离为π时，则B、C的距离为2π，C、D之间的距离为3π，
所以A、D之间的距离为π+2π+3π＝6π，
又因为点A表示的数为π，
所以点D所表示的数为π+6π＝7π，
②当A、B的距离为2π时，则B、C的距离为π，C、D之间的距离为2π×3＝6π，
所以A、D之间的距离为2π+π+6π＝9π，
又因为点A表示的数为π，
所以点D所表示的数为π+9π＝10π，
答：点D表示的数为7π或10π．
【点评】本题考查数轴表示数，无理数的意义，掌握数轴上两点距离的计算方法是解决问题的前提．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/10/14 9:06:31；用户：492175055；邮箱：492175055@qq.cm；学号：5783273