安徽省宣城2024-2025学年数学九年级第一学期开学统考试题【含答案】

这是一份安徽省宣城2024-2025学年数学九年级第一学期开学统考试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，矩形ABCD的边长AD=3，AB=2，E为AB的中点，F在边BC上，且BF=2FC，AF分别与DE、DB相交于点M，N，则MN的长为（ ）
A．B．C．D．
2、（4分）下列方程中属于一元二次方程的是（ ）
A．B．C．D．
3、（4分）如图，有一块菱形纸片ABCD，沿高DE剪下后拼成一个矩形，矩形的相邻两边DC和DE的长分别是5，1．则EB的长是（ ）
A．0.5B．1C．1.5D．2
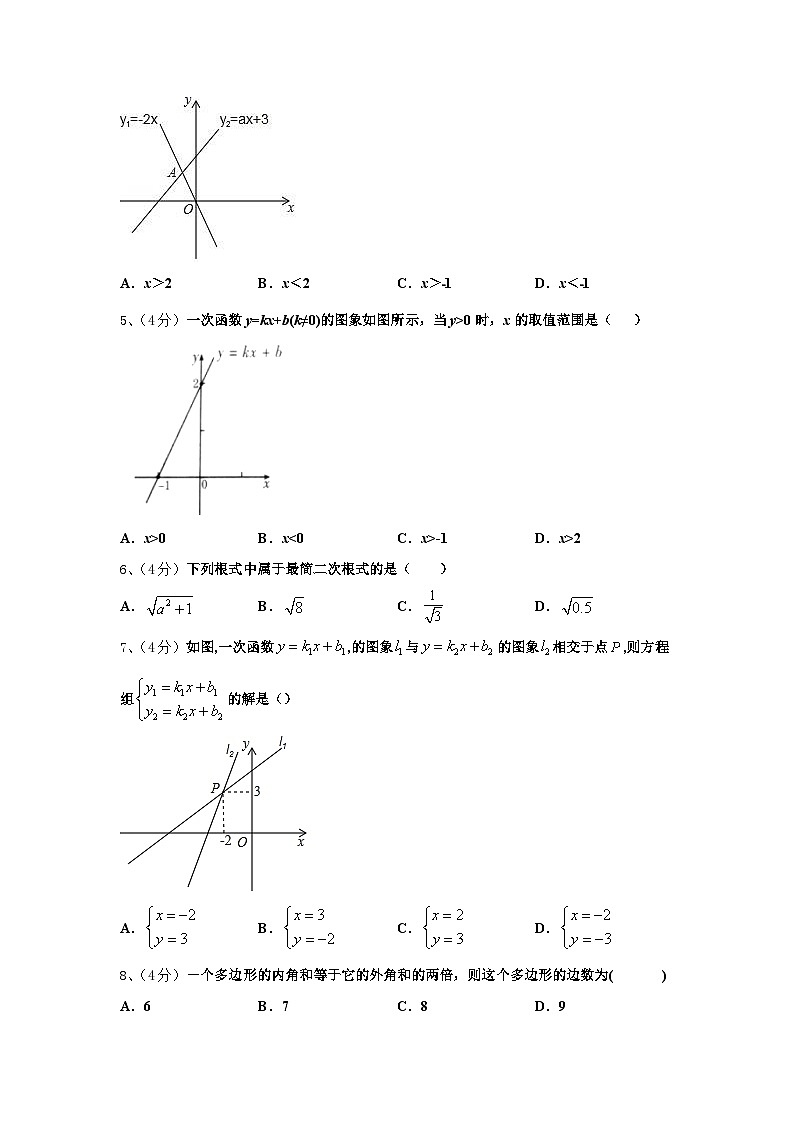
4、（4分）如图，函数 y1＝﹣2x 与 y2＝ax+3 的图象相交于点 A（m，2），则关于 x 的不等式﹣2x＞ax+3 的解集是（ ）
A．x＞2B．x＜2C．x＞﹣1D．x＜﹣1
5、（4分）一次函数y=kx+b(k≠0)的图象如图所示，当y>0时，x的取值范围是（ ）
A．x>0B．x<0C．x>-1D．x>2
6、（4分）下列根式中属于最简二次根式的是（ ）
A．B．C．D．
7、（4分）如图,一次函数,的图象与的图象相交于点,则方程组的解是（）
A．B．C．D．
8、（4分）－个多边形的内角和等于它的外角和的两倍，则这个多边形的边数为( )
A．6B．7C．8D．9
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若，则= ．
10、（4分）如图，直线y＝﹣x+4分别与x轴，y轴相交于点A，B，点C在直线AB上，D是坐标平面内一点，若以点O，A，C，D为顶点的四边形是菱形，则点D的坐标是_____．
11、（4分）如图，正方形ABCD的边长为，点E、F分别为边AD、CD上一点，将正方形分别沿BE、BF折叠，点A的对应点M恰好落在BF上，点C的对应点N给好落在BE上，则图中阴影部分的面积为__________；
12、（4分）已知点A（4，0），B（0，﹣2），C（a，a）及点D是一个平行四边形的四个顶点，则线段CD长的最小值为___．
13、（4分）如图1，边长为a的正方形发生形变后成为边长为a的菱形，如果这个菱形的一组对边之间的距离为h，我们把的值叫做这个菱形的“形变度”．例如，当形变后的菱形是如图2形状（被对角线BD分成2个等边三角形），则这个菱形的“形变度”为2：．如图3，正方形由16个边长为1的小正方形组成，形变后成为菱形，△AEF（A、E、F是格点）同时形变为△A′E′F′，若这个菱形的“形变度”k＝，则S△A′E′F′＝__
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，△ABC中，∠ACB＝90°，D是AB中点，过点B作直线CD的垂线，垂足为E，
求证：∠EBC＝∠A．
15、（8分）先化简，再求值：，其中
16、（8分）定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径。
（1）如图1，损矩形ABCD，∠ABC＝∠ADC＝90°，则该损矩形的直径是线段AC，同时我们还发现损矩形中有公共边的两个三角形角的特点，在公共边的同侧的两个角是相等的。如图1中：△ABC和△ABD有公共边AB，在AB同侧有∠ADB和∠ACB，此时∠ADB＝∠ACB；再比如△ABC和△BCD有公共边BC，在CB同侧有∠BAC和∠BDC，此时∠BAC＝∠BDC。请再找一对这样的角来 ＝
（2）如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由。
（3）在第（2）题的条件下，若此时AB＝，BD＝，求BC的长。
17、（10分）先化简，再求值：，其中x=，y=．
18、（10分）（1）如图（1），已知：正方形ABCD的对角线交于点O，E是AC上的一动点，过点A作AG⊥BE于G，交BD于F．求证：OE＝OF．
（2）在（1）的条件下，若E点在AC的延长线上，以上结论是否成立，为什么？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）一次函数的图象不经过__________象限
20、（4分）如图，将平行四边形ABCD沿对角线BD折叠，使点A落在点处若，则为______ ．
21、（4分）已知一次函数y=ax+b的图象经过点（﹣2，0）和点（0，﹣1），则不等式ax+b＞0的解集是_____．
22、（4分）若正数a是一元二次方程x2﹣5x+m=0的一个根，﹣a是一元二次方程x2+5x﹣m=0的一个根，则a的值是______．
23、（4分）一次函数y＝－2x＋4的图象与x轴交点坐标是______，与y轴交点坐标是_________
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在由边长为1个单位的长度的小正方形组成的网格图中，已知点O及△ABC的顶点均为网格线的交点
(1)在给定网格中，以O为位似中心，将△ABC放大为原来的三倍，得到请△A′B′C′，请画出△A′B′C′；
(2)B′C′的长度为___单位长度,△A′B′C′的面积为___平方单位。
25、（10分）体育课上，甲、乙两个小组进行定点投篮对抗赛，每组10人，每人投10次．下表是甲组成绩统计表：
(1)请计算甲组平均每人投进个数；
(1)经统计，两组平均每人投进个数相同且乙组成的方差为3.1．若从成绩稳定性角度看，哪一组表现更好？
26、（12分）如图，矩形的对角线相交于点.
（1）判断四边形的形状，并进行证明；（2）若，求四边形的面积.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
过F作FH⊥AD于H，交ED于O，于是得到FH=AB=1，根据勾股定理得到AF===，根据平行线分线段成比例定理得到，OH=AE=，由相似三角形的性质得到=，求得AM=AF=，根据相似三角形的性质得到=，求得AN=AF=，即可得到结论．
【详解】
过F作FH⊥AD于H，交ED于O，则FH=AB=1．
∵BF=1FC，BC=AD=3，
∴BF=AH=1，FC=HD=1，
∴AF===，
∵OH∥AE，
∴=，
∴OH=AE=，
∴OF=FH﹣OH=1﹣=，
∵AE∥FO，∴△AME∽△FMO，
∴=，∴AM=AF=，
∵AD∥BF，∴△AND∽△FNB，
∴=，
∴AN=AF=，
∴MN=AN﹣AM=﹣=，故选B．
构造相似三角形是本题的关键，且求长度问题一般需用到勾股定理来解决，常作垂线
2、A
【解析】
根据一元二次方程的定义直接进行判断
【详解】
解：只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程.符合这个定义.
故选：A
本题考查了一元二次方程的概念：只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程.
3、B
【解析】
直接利用菱形的性质得出AD的长，再利用勾股定理得出AE的长，进而利用平移的性质得出答案．
【详解】
解：∵有一块菱形纸片ABCD，DC＝5，
∴AD＝BC＝5，
∵DE＝2，∠DEA＝90°，
∴AE＝4，
则BE＝5﹣4＝2．
故选：B．
此题主要考查了图形的剪拼以及菱形的性质，正确得出AE的长是解题关键．
4、D
【解析】
因为函数与的图象相交于点A(m,2),把点A代入可求出,所以点A(－1,2),然后把点A代入解得, 不等式,
可化为,解不等式可得:,故选D.
5、C
【解析】
首先找到当y＞0时，图象所在位置，再根据图象可直接得到答案．
【详解】
当y＞0时，图象在x轴上方，
∵与x交于（-1，0），
∴y＞0时，自变量x的取值范围是x＞-1，
故选：C．
考查了一次函数与一元一次不等式，关键是能从图象中找到对应的直线．
6、A
【解析】
根据最简二次根式的定义选择即可.
【详解】
、是最简二次根式，故本选项正确；
、不是最简二次根式，故本选项错误；
、不是最简二次根式，故本选项错误；
、不是最简二次根式，故本选项错误.
故选：.
本题考查了最简二次根式，掌握最简二次根式的定义是解题的关键.
7、A
【解析】
根据图象求出交点P的坐标，根据点P的坐标即可得出答案．
【详解】
解：∵由图象可知：一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2的交点P的坐标是（-2，3），
∴方程组的解是，
故选A.
本题考查了对一次函数与二元一次方程组的关系的理解和运用，主要考查学生的观察图形的能力和理解能力，题目比较典型，但是一道比较容易出错的题目．
8、A
【解析】
根据题意得（n-2）•180=720，
解得：n=6，
故选A．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1．
【解析】
试题分析：有意义，必须，，解得：x=3，代入得：y=0+0+2=2，∴==1．故答案为1．
考点：二次根式有意义的条件．
10、（2，﹣2）或（6，2）
【解析】
分析：设点C的坐标为（x，﹣x+4）．分两种情况，分别以C在x轴的上方、C在x轴的下方做菱形，画出图形，根据菱形的性质找出点C的坐标即可得出D点的坐标．
详解：∵一次函数解析式为线y=﹣x+4，∴B（0，4），A（4，0），如图一．∵四边形OADC是菱形，设C（x，﹣x+4），∴OC=OA==4，整理得：x2﹣6x+8=0，解得x1=2，x2=4，∴C（2，2），∴D（6，2）；
如图二．∵四边形OADC是菱形，设C（x，﹣x+4），∴AC=OA==4，整理得：x2﹣8x+12=0，解得x1=2，x2=6，∴C（6，﹣2），∴D（2，﹣2）；
故答案为（2，﹣2）或（6，2）．

点睛：本题考查了一次函数图象上点的坐标特征以及菱形的性质，解题的关键是确定点C、D的位置．本题属于中档题，难度不大，在考虑菱形时需要分类讨论．
11、
【解析】
分析：设NE＝x，由对称的性质和勾股定理，用x分别表示出ON，OE，OM，在直角△OEN中用勾股定理列方程求x，则可求出△OBE的面积.
详解：连接BO.
∠ABE＝∠EBF＝∠FBC＝30°，AE＝1＝EM，BE＝2AE＝2.
∠BNF＝90°，∠NEO＝60°，∠EON＝30°，
设EN＝x，则EO＝2x，ON＝x＝OM，
∴OE＋OM＝2x＋x＝(2＋)x＝1.∴x＝＝2－.
∴ON＝x＝(2－)＝2－3.
∴S＝2S△BOE＝2×(×BE×ON)＝2×[×2×(2－3)]＝4－6.
故答案为.
点睛：翻折的本质是轴对称，所以注意对称点，找到相等的线段和角，结合勾股定理列方程求出相关的线段后求解.
12、3．
【解析】
讨论两种情形：①CD是对角线，②CD是边．CD是对角线时CF⊥直线y＝x时，CD最小．CD是边时，CD＝AB＝2，通过比较即可得出结论．
【详解】
如图，由题意得：点C在直线y＝x上，
①如果AB、CD为对角线，AB与CD交于点F，当FC⊥直线y＝x时，CD最小，
易知直线AB为y＝x﹣2，
∵AF＝FB，
∴点F坐标为（2，﹣1），
∵CF⊥直线y＝x，
设直线CF为y＝﹣x+b′，F（2，﹣1）代入得b′＝1，
∴直线CF为y＝﹣x+1，
由，解得：，
∴点C坐标．
∴CD＝2CF＝2×．
如果CD是平行四边形的边，则CD＝AB＝＞3，
∴CD的最小值为3．
故答案为3．
本题考查平行四边形的性质、坐标与图形的性质、垂线段最短、勾股定理等知识，学会分类讨论是解题的关键，灵活运用垂线段最短解决实际问题，属于中考常考题型．
13、
【解析】
求出形变前正方形的面积，形变后菱形的面积，两面积之比=菱形的“形变度”，求△AEF的面积，根据两面积之比=菱形的“形变度”，即可解答．
【详解】
如图，
在图2中,形变前正方形的面积为：a2,形变后的菱形的面积为：
∴菱形形变前的面积与形变后的面积之比：
∵这个菱形的“形变度”为2:，
∴菱形形变前的面积与形变后的面积之比=这个菱形的“形变度”，

∵若这个菱形的“形变度”k=，
∴
即
∴S△A′E′F′=.
故答案为：.
考查菱形的性质，读懂题目中菱形的“形变度”的概念是解题的关键.
三、解答题（本大题共5个小题，共48分）
14、详见解析
【解析】
由直角三角形斜边中线等于斜边的一半可得CD＝BD，从而可得∠DCB＝∠ABC，再根据直角三角形两锐角互余通过推导即可得出答案.
【详解】
∵∠ACB＝90°，
∴∠A+∠ABC＝90°，
又∵D是AB中点，
∴CD＝BD，
∴∠DCB＝∠ABC，
又∵∠E＝90°，
∴∠ECB+∠EBC＝90°，
∴∠EBC＝∠A．
本题考查了直角三角形斜边中线的性质，直角三角形两锐角互余，等腰三角形的性质，熟练掌握和灵活运用相关性质是解题的关键.
15、，
【解析】
根据分式的混合运算法则把原式化简，把x的值代入计算即可
【详解】
解：原式
当时，
原式
本题考查整式的混合运算-化简求值，解题的关键是明确整式的混合运算的计算方法．
16、（1）∠ABD=∠ACD；（2）四边形ACEF为正方形，理由见解析；（3）5.
【解析】
（1）以AD为公共边，有∠ABD=∠ACD；
（2）证明△ADC是等腰直角三角形，得AD=CD，则AE=CF，根据对角线相等的菱形是正方形可得结论；
（3）如图2，作辅助线构建直角三角形，证明△ABC≌△CHE，得CH=AB=3，根据平行线等分线段定理可得BG=GH=4，从而得结论.
【详解】
解：（1）由图1得：△ABD和△ADC有公共边AD，在AD同侧有∠ABD和∠ACD，此时∠ABD=∠ACD；
（2）四边形ACEF为正方形，理由是：
∵∠ABC=90°，BD平分∠ABC，
∴∠ABD=∠CBD=45°
∴∠DAC=∠CBD=45°
∵四边形ACEF是菱形，
∴AELCF，
∴∠ADC=90°，
∴△ADC是等腰直角三角形，
∴AD=CD，.AE=CF，
∴菱形ACEF是正方形；
（3）如图2，过D作DG⊥BC于G，过E作EH⊥BC，交BC的延长线于H，
∵∠DBG=45°，
∴△BDG是等腰直角三角形，BD=4，
∵BG=4，四边形ACEF是正方形，
∴AC=CE，∠ACE=90°，AD=DE，
易得△ABC≌△CHE，
∴CH=AB=3，AB//DG//EH，AD=DE，
∴BG=GH=4，
∴CG=4-3=1，
∴BC=BG+CG=4+1=5.
本题是四边形的综合题，也是新定义问题，考查了损矩形和损矩形的直径的概念，平行线等分线段定理，菱形的性质，正方形的判定等知识，认真阅读理解新定义，第3问有难度，作辅助线构建全等三角形是关键.
17、x+y，．
【解析】
试题分析：根据分式的减法和除法可以化简题目中的式子，然后将x、y的值代入即可解答本题．
试题解析：原式= ==x+y，
当x=，y==2时，原式=﹣2+2=．
18、（1）详见解析；（2）以上结论仍然成立．
【解析】
（1）利用正方形的性质得OA＝OB，∠AOB＝∠BOC＝90°，则利用等角的余角相等得到∠GAE＝∠OBE，则可根据”ASA“判断△AOF≌△BOE，从而得到OF＝OE；
（2）同样方法证明△AOF≌△BOE，仍然得到OF＝OE．
【详解】
解：（1）证明：∵四边形ABCD为正方形，
∴OA＝OB，∠AOB＝∠BOC＝90°，
∵AG⊥BE于点G，
∴∠AGE＝90°，
∴∠GAE＝∠OBE，
在△AOF和△BOE中，，
∴△AOF≌△BOE（ASA），
∴OF＝OE；
（2）解：以上结论仍然成立．理由如下：
同样可证明△AOF≌△BOE（ASA），所以OF＝OE．
本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质；两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、二
【解析】
根据一次函数的图像即可求解.
【详解】
一次函数过一三四象限，故不经过第二象限.
此题主要考查一次函数的图像，解题的关键是熟知一次函数的性质.
20、105°
【解析】
由平行四边形的性质和折叠的性质，得出∠ADB=∠BDG=∠DBG，由三角形的外角性质求出∠BDG=∠DBG=∠1=25°，再由三角形内角和定理求出∠A，即可得到结果．
【详解】
∵AD∥BC，
∴∠ADB=∠DBG，
由折叠可得∠ADB=∠BDG，
∴∠DBG=∠BDG，
又∵∠1=∠BDG+∠DBG=50°，
∴∠ADB=∠BDG=25°，
又∵∠2=50°，
∴△ABD中,∠A=105°，
∴∠A′=∠A=105°，
故答案为：105°.
本题主要考查了翻折变换（折叠问题），平行四边形的性质，熟练掌握折叠性质和平行四边形额性质是解答本题的关键.
21、x＜﹣2
【解析】
根据点A和点B的坐标得到一次函数图象经过第二、三、四象限，根据函数图象得到当x＞-2时，图象在x轴上方，即y＞1．
【详解】
解：∵一次函数y=ax+b的图象经过（-2，1）和点（1，-1），
∴一次函数图象经过第二、三、四象限，
∴当x＜-2时，y＞1，即ax+b＞1，
∴关于x的不等式ax+b＜1的解集为x＜-2．故答案为：x＜-2．
本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）1的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
22、1
【解析】
试题解析：∵a是一元二次方程x2-1x+m=0的一个根，-a是一元二次方程x2+1x-m=0的一个根，
∴a2-1a+m=0①，a2-1a-m=0②，
①+②，得2（a2-1a）=0，
∵a＞0，
∴a=1．
考点：一元二次方程的解．
23、 （2，0） （0，4）
【解析】把y=0代入y=2x+4得：0=2x+4，x=−2，
令x=0，代入y=2x+4解得y=4，
∴一次函数y=2x+4的图象与y轴交点坐标这(0,4)，
即一次函数y=2x+4与x轴的交点坐标是(−2,0)，与y轴交点坐标这(0,4).
二、解答题（本大题共3个小题，共30分）
24、（1）如图所示；见解析；（2）3，9；
【解析】
（1）利用位似图形的性质得出对应点坐标进而得出答案；
（2）根据勾股定理和三角形的面积公式即可得到结论．
【详解】
(1)如图所示：△A′B′C′即为所求：
(2)如图所示：B′C′的长度= =3 ；
∵A′C′=3，
∴△A′B′C′的面积为= ×3×6=9平方单位，
故答案为：3，9.
此题考查作图-位似变换，勾股定理和三角形的面积公式，解题关键在于掌握作图法则
25、 (1)甲组平均每人投进个数为7个；(1)乙组表现更好．
【解析】
（1）加权平均数：若n个数x1，x1，x3，…，xn的权分别是w1，w1，w3，…，wn，则x1w1+x1w1+…+xnwnw1+w1+…+wn叫做这n个数的加权平均数，根据加权平均数的定义计算即可.
（1）用“先平均，再求差，然后平方，最后再平均”得到的结果表示一组数据偏离平均值的情况，这个结果叫方差，通常用s1来表示，根据方差的计算公式结合平均数进行计算即可．
【详解】
解：(1)甲组平均每人投进个数：(个；
(1)甲组方差：，
乙组的方差为3.1，3.1＜3.4
所以从成绩稳定性角度看，乙组表现更好．
本题考查了方差的计算以及方差越小数据越稳定，正确运用方差公式进行计算是解题的关键．
26、（1）四边形是菱形，见解析；（2）.
【解析】
（1）先证四边形是平行四边形，再证其一组邻边相等即可；
（2）求出OE的长，再根据菱形的面积公式求解.
【详解】
解：四边形是菱形
四边形是平行四边形
四边形是矩形
平行四边形为菱形
连接交于
四边形是矩形
由可知，四边形是菱形
在中，
本题考查了菱形的判定及其面积，熟练掌握菱形的判定方法及面积公式是解题的关键.
题号
一
二
三
四
五
总分
得分
投进个数
10个
8个
6个
4个
人数
1个
5人
1人
1人