安徽省宣城市奋飞学校2024年九上数学开学经典试题【含答案】

这是一份安徽省宣城市奋飞学校2024年九上数学开学经典试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，点O为四边形ABCD内任意一点，E，F，G，H分别为OA，OB，OC，OD的中点，则四边形EFGH的周长为（ ）
A．9B．12C．18D．不能确定
2、（4分）若一元二次方程ax2+bx+c=0(a≠0)有一个根为-1，则a-b+c的值是( )
A．-1B．1C．0D．不能确定
3、（4分）代数式2x，，x+，中分式有（ ）
A．1个B．2个C．3个D．4个
4、（4分）使代数式有意义的x的取值范围是（ ）
A．x≥0B．C．x取一切实数D．x≥0且
5、（4分）下列事件为随机事件的是（ ）
A．367人中至少有2人生日相同B．打开电视，正在播广告
C．没有水分，种子发芽D．如果、都是实数，那么
6、（4分）下列说法正确的是( )
A．的相反数是B．2是4的平方根
C．是无理数D．计算：
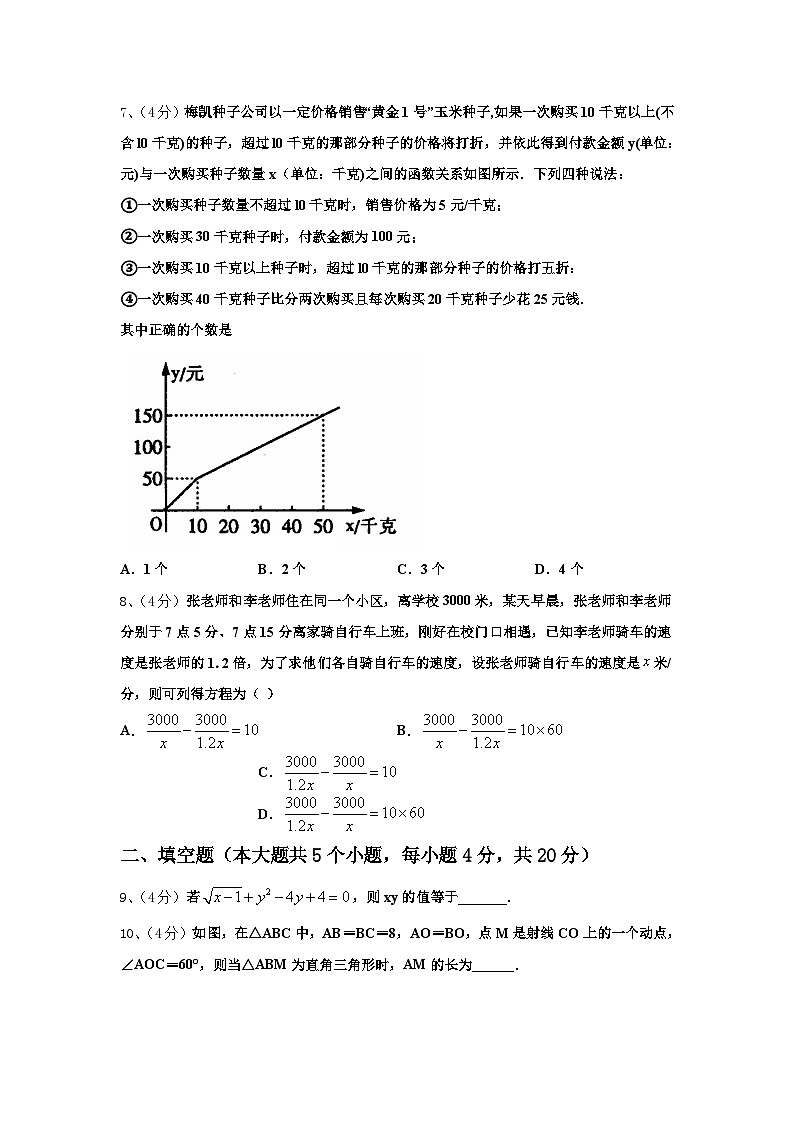
7、（4分）梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子，超过l0千克的那部分种子的价格将打折，并依此得到付款金额y(单位：元)与一次购买种子数量x（单位：千克)之间的函数关系如图所示．下列四种说法：
①一次购买种子数量不超过l0千克时，销售价格为5元/千克；
②一次购买30千克种子时，付款金额为100元；
③一次购买10千克以上种子时，超过l0千克的那部分种子的价格打五折：
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱．
其中正确的个数是
A．1个B．2个C．3个D．4个
8、（4分）张老师和李老师住在同一个小区，离学校3000米，某天早晨，张老师和李老师分别于7点5分、7点15分离家骑自行车上班，刚好在校门口相遇，已知李老师骑车的速度是张老师的1.2倍，为了求他们各自骑自行车的速度，设张老师骑自行车的速度是米/分，则可列得方程为（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若，则xy的值等于_______.
10、（4分）如图，在△ABC中，AB＝BC＝8，AO＝BO，点M是射线CO上的一个动点，∠AOC＝60°，则当△ABM为直角三角形时，AM的长为______．
11、（4分）同一坐标系下双曲线y与直线ykx一个交点为坐标为3,1，则它们另一个交点为坐标为_____．
12、（4分）一次函数与的图象如图，则的解集是__．
13、（4分）若代数式的值大于﹣1且小于等于2，则x的取值范围是_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图：在中，平分，且，于点，于点.
(1)求证：；
(2)若，，求的长.
15、（8分）（1）计算：
（2）已知：如图，在△ABC中，AB＝AC，点D、E、F分别是△ABC各边的中点，求证：四边形AEDF是菱形．
16、（8分）本学期开学后，某校为了宣传关于新冠肺炎的防控知识，需印制若干份资料，印刷厂有甲、乙两种收费方式，甲种方式每份资料收费0.1元，另需收取制版费20元；乙种方式每份资料收费0.15元，不需要收取制版费．
（1）设资料印刷的费用为y元，印刷的数量为x份，请分别写出两种收费方式下y与x之间的函数关系式；
（2）该校某年级每次需印制100～600（含100和600）份资料，选择哪种印刷方式较合算？
17、（10分）计算：（-）0+（-4）-2-|-|
18、（10分）如图1，为坐标原点，矩形的顶点，，将矩形绕点按顺时针方向旋转一定的角度得到矩形，此时边、直线分别与直线交于点、．
（1）连接，在旋转过程中，当时，求点坐标．
（2）连接，当时，若为线段中点，求的面积．
（3）如图2，连接，以为斜边向上作等腰直角，请直接写出在旋转过程中的最小值．

B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若正多边形的一个内角等于150°，则这个正多边形的边数是______．
20、（4分）如图,矩形的对角线相交于点,过点作交于点,若,的面积为6,则___．
21、（4分）已知关于x的方程x2+mx-2=0的两个根为x1、x2，若x1+x2-x1x2=6，则m=______．
22、（4分）甲、乙两人面试和笔试的成绩如下表所示：
某公司认为，招聘公关人员，面试成绩应该比笔试成绩重要，如果面试和笔试的权重分别是6和4，根据两人的平均成绩，这个公司将录取________。
23、（4分）王明在计算一道方差题时写下了如下算式：，则其中的____________.
二、解答题（本大题共3个小题，共30分）
24、（8分）某中学为了预防流行性感冒，对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量与时间成正比例．药物燃烧后，y与x成反比例（如图所示），现测得药物6min燃毕，此时室内空气中每立方米的含药量为4mg，
（1）写出药物燃烧前后，y与x之间的函数表达式；
（2）研究表明，当空气中每立方米的含药量低于1.6mg时学生方可进教室，那么从消毒开始，至少需要经过多少分钟，学生方能回到教室？
（3）研究表明，当空气中每立方米的含药量不低于2mg且持续时间不低于9min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？
25、（10分）如图所示，有一长方形的空地，长为米，宽为米，建筑商把它分成甲、乙、丙三部分，甲和乙为正方形.现计划甲建筑成住宅区，乙建成商场丙开辟成公园.
请用含的代数式表示正方形乙的边长； ；
若丙地的面积为平方米，请求出的值.
26、（12分）列方程解题：据专家预测今年受厄尔尼诺现象影响，我国大部分地区可能遇到洪涝灾害．进入防汛期前，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话：
“你们是用9天完成4800米长的大坝加固任务的”？
“我们加固600米后采用新的加固模式，这样每天加固长度是原来的2倍”，
通过这段对话请你求出该地驻军原来每天加固的米数．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
由三角形中位线定理可得EF=AB，FG=BC，HG=DC，EH=AD，再根据题目给出的已知数据即可求出四边形EFGH的周长．
【详解】
解：∵E，F分别为OA，OB的中点，
∴EF是△AOB的中位线，
∴EF=AB=3，
同理可得：FG=BC=5，HG=DC=6，EH=AD=4，
∴四边形EFGH的周长为=3+5+6+4=18，
故选C．
本题考查了中点四边形的性质和三角形中位线定理的运用，解题的关键是根据三角形中位线定理得到四边形EFGH各边是原四边形ABCD的各边的一半．
2、C
【解析】
将x=-1代入方程，就可求出a-b+c的值.
【详解】
解：将x=-1代入方程得， a-b+c=0
故答案为：C
本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
3、A
【解析】
直接利用分式的定义分析得出答案．
【详解】
解：代数式2x，，x+，中分式有：．
故选A．
本题考查了分式的定义，正确把握定义是解题关键．
4、D
【解析】
试题分析：根据题意可得：当x≥0且3x﹣1≠0时，代数式有意义，
解得：x≥0且．故选D．
考点：1.二次根式有意义的条件；2.分式有意义的条件．
5、B
【解析】
根据事件发生的可能性大小判断相应事件的类型即可．
【详解】
A. 367人中至少有2人生日相同 ，是必然事件，故A不符合题意；
B. 打开电视，正在播广告，是随机事件，故B符合题意；
C. 没有水分，种子发芽， 是不可能事件，故C不符合题意；
D. 如果、都是实数，那么，是必然事件，故D不符合题意.
故选B.
本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
6、B
【解析】
根据只有符号不同的两个数互为相反数；开方运算，可得答案．
【详解】
A. 只有符号不同的两个数互为相反数，故A正确；
B. 2是4的平方根，故B正确；
C.=3是有理数，故C错误；
D. =3≠-3，故D错误；
故选B.
本题考查了相反数，平方根，立方根的知识点，解题的关键是熟练掌握相反数，平方根，立方根的定义.
7、D
【解析】
①由图可知，购买10千克种子需要50元，由此求出一次购买种子数量不超过10千克时的销售价格；
②由图可知，超过10千克以后，超过的那部分种子的单价降低，而由购买50千克比购买10千克种子多付100元，求出超过10千克以后，超过的那部分种子的单价，再计算出一次购买30千克种子时的付款金额；
③根据一次购买10千克以上种子时，超过10千克的那部分种子的价格为2.5元/千克，而2.5÷5=0.5，所以可以求出打的折数；
④先求出一次购买40千克种子的付款金额为125元，再求出分两次购买且每次购买20千克种子的付款金额为150元，然后用150减去125，即可求出一次购买40千克种子比分两次购买且每次购买20千克种子少花的钱数．
解：①由图可知，一次购买种子数量不超过10千克时，销售价格为：50÷10=5元/千克，正确；
②由图可知，超过10千克的那部分种子的价格为：（150-50）÷（50-10）=2.5元/千克，所以，一次购买30千克种子时，付款金额为：50+2.5×（30-10）=100元，正确；
③由于一次购买10千克以上种子时，超过10千克的那部分种子的价格为2.5元/千克，而2.5÷5=0.5，所以打五折，正确；
④由于一次购买40千克种子需要：50+2.5×（40-10）=125元，
分两次购买且每次购买20千克种子需要：2×[50+2.5×（20-10）]=150元，
而150-125=25元，
所以一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱，正确．
故选D．
8、A
【解析】
设张老师骑自行车的速度是x米/分，则李老师骑自行车的速度是1．2x米/分，根据题意可得等量关系：张老师行驶的路程3000÷他的速度-李老师行驶的路程3000÷他的速度=10分钟，根据等量关系列出方程即可．
【详解】
设张老师骑自行车的速度是x米/分，由题意得：
，
故选：A．
此题主要考查了由实际问题抽象出分式方程，关键是正确理解题意，表示出李老师和张老师各行驶3000米所用的时间，根据时间关系列出方程．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
直接利用偶次方的性质以及二次根式的性质得出x，y的值进而得出答案．
【详解】
解：∵，
∴x-1=0， y-1=0，
解得：x=1，y=1，
则xy=1．
此题主要考查了完全平方公式，偶次方的性质以及二次根式的性质，正确掌握相关性质是解题关键．
10、1或1或1
【解析】
分三种情况讨论：①当M在AB下方且∠AMB=90°时，②当M在AB上方且∠AMB=90°时，③当∠ABM=90°时，分别根据含30°直角三角形的性质、直角三角形斜边的中线的性质或勾股定理，进行计算求解即可．
【详解】
如图1，当∠AMB=90°时，
∵O是AB的中点，AB=8，
∴OM=OB=1，
又∵∠AOC=∠BOM=60°，
∴△BOM是等边三角形，
∴BM=BO=1，
∴Rt△ABM中，AM==；
如图2，当∠AMB=90°时，
∵O是AB的中点，AB=8，
∴OM=OA=1，
又∵∠AOC=60°，
∴△AOM是等边三角形，
∴AM=AO=1；
如图3，当∠ABM=90°时，
∵∠BOM=∠AOC=60°，
∴∠BMO=30°，
∴MO=2BO=2×1=8，
∴Rt△BOM中，BM==，
∴Rt△ABM中，AM==．
综上所述，当△ABM为直角三角形时，AM的长为或或1．故答案为或或1．
11、
【解析】
反比例函数的图象是中心对称图形，则经过原点的直线的两个交点一定关于原点对称．
【详解】
解：∵同一坐标系下双曲线y与直线ykx一个交点为坐标为3,1，
∴另一交点的坐标是（-3，1）．
故答案是：（-3，1）．
本题主要考查了反比例函数图象的中心对称性，要求同学们要熟练掌握．
12、
【解析】
不等式kx+b-（x+a）＞0的解集是一次函数y1=kx+b在y2=x+a的图象上方的部分对应的x的取值范围，据此即可解答．
【详解】
解：不等式的解集是．
故答案为：．
本题考查了一次函数的图象与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
13、﹣1≤x＜1．
【解析】
先根据题意得出关于x的不等式组，求出x的取值范围即可．
【详解】
解：根据题意，得：
解不等式①，得：x＜1，
解不等式②，得：x≥-1，
所以-1≤x＜1，
故答案为：-1≤x＜1．
本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）证明见解析；（2）
【解析】
（1）根据角平分线的性质得到DE＝DF，证明Rt△BDE≌Rt△CDF，根据全等三角形的性质得到∠B＝∠C，根据等腰三角形的判定定理证明；
（2）根据直角三角形的性质求出AC，根据勾股定理计算即可．
【详解】
（1）证明：∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE＝DF，
在Rt△BDE和Rt△CDF中， ，
∴Rt△BDE≌Rt△CDF，
∴∠B＝∠C，
∴AB＝AC；
（2）∵AD平分∠BAC，BD＝CD，
∴AD⊥BC，
∵∠DAC＝30°，
∴AC＝2DC＝8，
∴AD＝．
本题考查的是全等三角形的判定和性质、角平分线的性质，掌握全等三角形的判定定理和性质定理是解题的关键．
15、 (1) ；（2）详见解析
【解析】
（1）首先计算绝对值、化简二次根式、立方根，然后再计算加减即可；
（2）利用中位线定理可得ED∥AC，ED=AC，DF∥AB，DF=AB，利用两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形，再证明ED=FD可得结论．
【详解】
（1）
=
=；
（2）证明：∵D，E，F分別是BC，AB，AC的中点，
∴ED∥AC，ED=AC，DF∥AB，DF=AB，
∵ED∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∵AB=AC，
∴ED=FD，
∴四边形AEDF是菱形．
此题主要考查了实数的计算和菱形的判定，关键是掌握三角形的中位线平行于第三边，并且等于第三边的一半；一组邻边相等的平行四边形是菱形．
16、（1）y1＝0.1x＋20；y2＝0.15x；（2）当100≤x＜400时，选择乙种方式较合算；当x＝400时，甲、乙两种方式一样合算；当400＜x≤600时，选择甲种方式较合算
【解析】
（1）根据题意，可以直接写出两种收费方式下y与x之间的函数关系式；
（2）根据题意，可知刚开始乙种印刷方式合算，故令（1）中的两个函数值相等，求出相应的x的值，然后即可写出x在什么范围内，选择哪种印刷方式合算．
【详解】
解：（1）甲种收费的函数关系式是y1＝0.1x＋20；
乙种收费的函数关系式是y2＝0.15x；
（2）由题意，当y1＞y2时，0.1x＋20＞0.15x，得x＜400；
当y1＝y2时，0.1x＋20＝0.15x，得x＝400；
当y1＜y2时，0.1x＋20＜0.15x，得x＞400；
答：当100≤x＜400时，选择乙种方式较合算；
当x＝400时，甲、乙两种方式一样合算；
当400＜x≤600时，选择甲种方式较合算．
本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质解答．
17、1
【解析】
先计算0指数幂、负指数幂和绝对值，再根据有理数加减混合运算法则计算即可得到结果．
【详解】
解：原式=
=1+-
=1．
此题考查了实数加减混合运算，熟练掌握运算法则是解本题的关键．
18、（1）P（﹣4，6）；（2）；（3）
【解析】
（1）利用∠PAO＝∠POA得出PA＝PO，进而得出AE＝EO＝4，即可得出P点坐标；
（2）首先得出Rt△OCQ≌Rt△OC'Q（HL），进而利用平行线的性质求出∠POQ＝∠PQO，即可得出BP＝PO，再利用勾股定理得出PQ的长，进而求出△OPQ的面积；
（3）先构造一组手拉手的相似三角形，将CM的长转化为，然后通过垂线段最短及全等三角形求解即可．
【详解】
解：如图1，过点P作PE⊥AO于点E，
∵，
∴AO＝8，
∵∠PAO＝∠POA
∴PA＝PO，
∵PE⊥AO，
∴AE＝EO＝4，
∴P（﹣4，6）；
（2）如图2，在Rt△OCQ和Rt△OC'Q中，
，
∴Rt△OCQ≌Rt△OC'Q（HL），
∴∠OQC＝∠OQC'，
又∵OP∥C'Q，
∵∠POQ＝∠OQC'，
∴∠POQ＝∠PQO，
∴PO＝PQ，
∵点P为BQ的中点，
∴BP＝QP，
∴设BP＝OP＝x，
在Rt△OPC中，OP 2＝PC 2＋ OC 2，
∴x2＝（8﹣x）2＋62，
解得：x＝．
故S△OPQ＝×CO×PQ＝×6×＝．
（3）如图3，连接CM、AC，在AC的右侧以AC为腰，∠ACG为直角作等腰直角三角形ACG，连接QG，
∵△AMQ与△ACG为等腰直角三角形，
∴ ，∠MAQ＝∠CAG＝45°，
∴，∠MAC＝∠QAG
∴△MAC∽△QAC，
∴，
∴，
∵点Q在直线BC上，
∴当GQ⊥BC时，GQ取得最小值，
如图3，作GH⊥BC，则GQ的最小值为线段GH的长，
∵∠ACG＝∠B＝90°，
∴∠ACB＋∠GCH＝∠ACB＋∠BAC＝90°，
∴∠GCH＝∠BAC，
又∵∠B＝∠GHC＝90°，AC＝CG，
∴△ABC≌△CHG（AAS）
∴GH＝BC＝8
∴GQ的最小值为8，
∴CM的最小值为．
此题主要考查了矩形的判定与性质以及全等三角形的判定与性质、勾股定理、三角形面积求法等知识，正确得出PO＝PQ是解题关键，最后一小问需要构造相似三角形进行转化，有点难度．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1．
【解析】
首先根据求出外角度数，再利用外角和定理求出边数．
【详解】
正多边形的一个内角等于，
它的外角是：，
它的边数是：．
故答案为：1．
此题主要考查了多边形的外角与内角，做此类题目，首先求出正多边形的外角度数，再利用外角和定理求出求边数．
20、
【解析】
首先连接EC，由题意可得OE为对角线AC的垂直平分线，可得CE=AE，S△AOE=S△COE=2，继而可得AE•BC=1，则可求得AE的长，即EC的长，然后由勾股定理求得答案．
【详解】
解：连接EC.
∵四边形ABCD是矩形
∴AO=CO，且OE⊥AC，
∴OE垂直平分AC
∴CE=AE，S△AOE=S△COE=2，
∴S△AEC=2S△AOE=1．
∴AE•BC=1，
又∵BC=4，
∴AE=2，
∴EC=2．
∴BE=
故答案为：
本题考查了矩形的性质、勾股定理以及三角形的面积问题．此题难度适中，正确做出图形的辅助线是解题的关键．
21、-2
【解析】
利用根与系数的关系求出两根之和与两根之积，代入所求式子中计算即可求出值．
【详解】
解：依题意得：x1+x1=-m，x1x1=-1．
所以x1+x1-x1x1=-m-（-1）=6
所以m=-2．
故答案是：-2．
此题考查了一元二次方程根与系数的关系，一元二次方程ax1+bx+c=0（a≠0）的根与系数的关系为：x1+x1=-，x1•x1=．
22、乙
【解析】
根据题意先算出甲、乙两位候选人的加权平均数，再进行比较，即可得出答案．
【详解】
甲的平均成绩为：（86×6+90×4）÷10=87.6（分），
乙的平均成绩为：（92×6+83×4）÷10=88.4（分），
因为乙的平均分数最高，
所以乙将被录取．
故答案为乙．
此题考查了加权平均数的计算公式，注意，计算平均数时按6和4的权进行计算.
23、1.865
【解析】
先计算出4个数据的平均数，再计算出方差即可.
【详解】
∵，
∴
=
=
=
=
=1.865.
故答案为：1.865.
此题主要考查了方差的计算，求出平均数是解决此题的关键.
二、解答题（本大题共3个小题，共30分）
24、（1）药物燃烧时y关于x的函数关系式为：；药物燃烧后y关于x的函数关系式为：；（2）至少需要15分钟后学生方能回到教室；（3）此次消毒有效.
【解析】
（1）药物燃烧时，设出y与x之间的解析式y＝k1x，把点（6，4）代入即可；药物燃烧后，设出y与x之间的解析式，把点（6，4）代入即可；
（2）把y＝1.6代入反比例函数解析式，求出相应的x即可判断；
（3）把y＝2代入正比例函数解析式和反比例函数解析式，求出相应的x，两数之差与9进行比较，不小于9就有效．
【详解】
解：（1）设药物燃烧时y关于x的函数关系式为y＝k1x (k1≠0)，
代入（6，4）得：4＝6k1，解得：，
∴药物燃烧时y关于x的函数关系式为：；
设药物燃烧后y关于x的函数关系式为，
代入（6，4）得，解得：k2＝24，
∴药物燃烧后y关于x的函数关系式为：；
（2）将y=1.6代入，解得：x=15，
所以从消毒开始，至少需要15分钟后学生方能回到教室；
（3）把y＝2代入，得：x＝3，
把y＝2代入，得：x＝12，
∵12−3＝9，
所以此次消毒有效．
本题考查了一次函数和反比例函数的综合应用，现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式．
25、（1）（x−12）米；（2）的值为20或1.
【解析】
（1）由甲和乙为正方形，且该地长为x米，宽为12米，可得出丙的长，也是乙的边长；
（2）由（1）求得丙的长，再求出丙的宽，即可得出丙的面积，由此列出方程，求解即可．
【详解】
解：（1）因为甲和乙为正方形，结合图形可得丙的长为：（x−12）米．
同样乙的边长也为（x−12）米，
故答案为：（x−12）米；
（2）结合（1）得，丙的长为：（x−12）米，丙的宽为12−（x−12）=（24−x）米，所以丙的面积为：（x−12）（24−x），
列方程得，（x−12）（24−x）＝32
解方程得x1＝20，x2＝1．
答：的值为20或1.
本题考查了一元二次方程的应用，解题的关键是表示出有关的线段的长，难度不大．
26、该建筑队原来每天加固300米．
【解析】
设原来每天加固x米，则采用新的加固技术后每天加固2x米，然后依据共用9天完成任务进行解答即可．
【详解】
解：设原来每天加固x米，则采用新的加固技术后每天加固2x米．
根据题意得：
解得：x＝300，
经检验x＝300是分式方程的解．
答：该建筑队原来每天加固300米．
本题主要考查的是分式方程的应用，找出题目的等量关系是解题的关键．
题号
一
二
三
四
五
总分
得分
候选人
甲
乙
测试成绩（百分制）
面试成绩
86
92
笔试成绩
90
83