北京师范大亚太实验学校2024-2025学年数学九上开学达标检测试题【含答案】

这是一份北京师范大亚太实验学校2024-2025学年数学九上开学达标检测试题【含答案】，共23页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，将边长为2的正方形OABC放在平面直角坐标系中，O是原点，点A的横坐标为1，则点C的坐标为（ ）
A．（﹣2，1）B．（﹣1，2）C．（，﹣1）D．（﹣，1）
2、（4分）下列成语描述的事件为随机事件的是（ ）
A．水涨船高 B．守株待兔 C．水中捞月 D．缘木求鱼
3、（4分）若一个多边形从一个顶点出发的对角线共有3条，则这个多边形的内角和为（ ）
A．360°B．540°C．720°D．1080°
4、（4分）已知正比例函数（）的函数值y随x的增大而减小，则一次函数的图像经过的象限为 （ ）
A．二、三、四 B．一、二、四 C．一、三、四 D．一、二、三
5、（4分）如图所示，在平行直角坐标系中，▱OMNP的顶点P坐标是（3，4），顶点M坐标是（4，0）、则顶点N的坐标是（ ）
A．N（7，4）B．N（8，4）C．N（7，3）D．N（8，3）
6、（4分）以下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（ ）
A．2，3，4B．， ， C．1， ，2D．7，8，9
7、（4分）点A、B、C、D在同一平面内，从AB∥CD，AB=CD，AD∥BC这三条件中任选两个能使四边形ABCD是平行四边形的选法有（ ）
A．1种B．2种C．3种D．以上都不对
8、（4分）下列各组长度的线段中，可以组成直角三角形的是（ ）
A．1,2,3B．1,,3C．5,6,7D．5,12,13
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若，则的值为______.
10、（4分）一列数，，，，其中，（为不小于的整数），则___．
11、（4分）如图，AB∥CD，则∠1+∠3—∠2的度数等于 __________．
12、（4分）如图，△A1B1A2，△A2B2A3，△A3B3A4，...，△AnBnAn+1都是等腰直角三角形，其中点A1、A2、…、An，在x轴上，点B1、B2、…Bn在直线y=x上，已知OA1=1，则OA2019的长是_____.
13、（4分）学校篮球集训队11名队员进行定点投篮训练，将11名队员在1分钟内投进篮筐的球数由小到大排序后为6，7，8，9，9，9，9，10，10，10，12，这组数据的众数和中位数分别是______________.
三、解答题（本大题共5个小题，共48分）
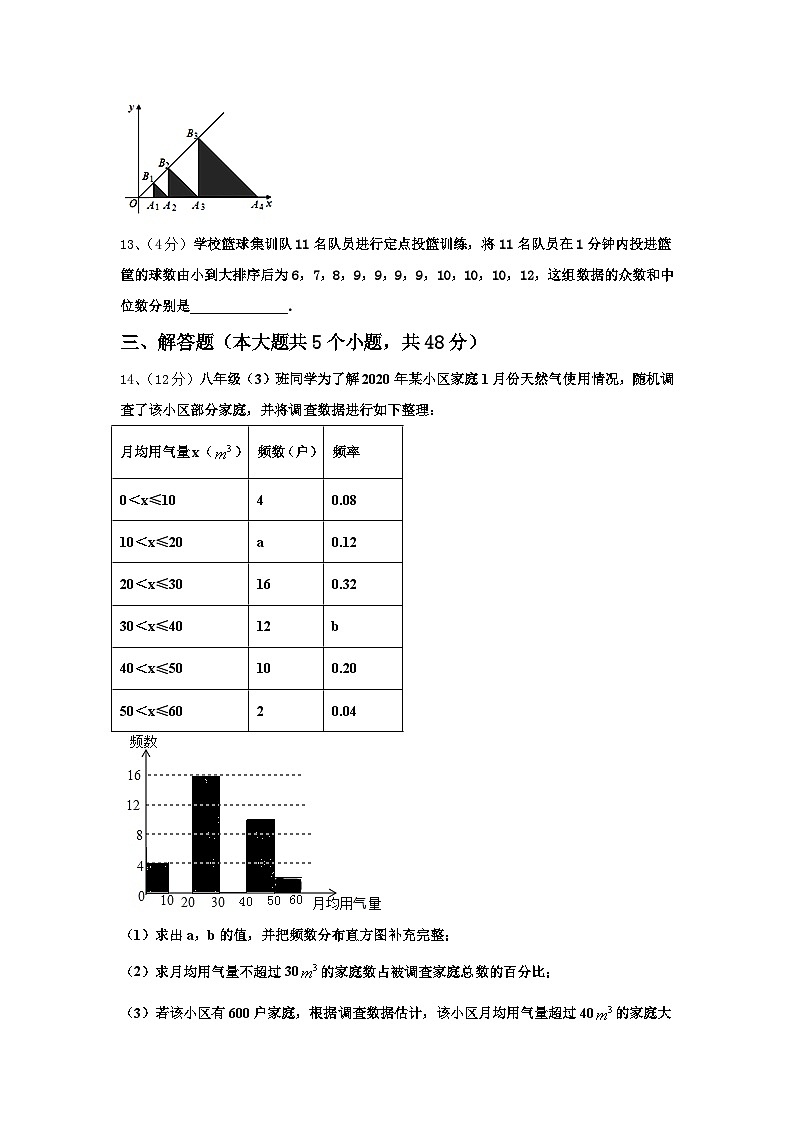
14、（12分）八年级（3）班同学为了解2020年某小区家庭1月份天然气使用情况，随机调查了该小区部分家庭，并将调查数据进行如下整理：
（1）求出a，b的值，并把频数分布直方图补充完整；
（2）求月均用气量不超过30的家庭数占被调查家庭总数的百分比；
（3）若该小区有600户家庭，根据调查数据估计，该小区月均用气量超过40的家庭大约有多少户？
15、（8分）下面是某同学对多项式（x2﹣4x+2）（x2﹣4x+6）+4进行因式分解的过程
解：设x2﹣4x＝y，
原式＝（y+2）（y+6）+4 （第一步）
＝y2+8y+16 （第二步）
＝（y+4）2（第三步）
＝（x2﹣4x+4）2（第四步）
（1）该同学第二步到第三步运用了因式分解的 （填序号）．
A．提取公因式 B．平方差公式
C．两数和的完全平方公式 D．两数差的完全平方公式
（2）该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？ ．（填“是”或“否”）如果否，直接写出最后的结果 ．
（3）请你模仿以上方法尝试对多项式（x2﹣2x）（x2﹣2x+2）+1进行因式分解．
16、（8分）问题：探究函数y＝|x|﹣2的图象与性质．
小华根据学习函数的经验，对函数y＝|x|﹣2的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）在函数y＝|x|﹣2中，自变量x可以是任意实数；
（2）如表是y与x的几组对应值
①m等于多少；
②若A（n，2018），B（2020，2018）为该函数图象上不同的两点，则n等于多少；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并根据描出的点画出该函数的图象；根据函数图象可得：该函数的最小值为多少；该函数图象与x轴围成的几何图形的面积等于多少；
（4）已知直线y1＝x﹣与函数y＝|x|﹣2的图象交于C，D两点，当y1≥y时，试确定x的取值范围．
17、（10分）（感知）如图①，四边形ABCD、CEFG均为正方形．可知BE=DG．
（拓展）如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．
（应用）如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD延长线上．若AE=2ED，∠A=∠F，△EBC的面积为8，菱形CEFG的面积是_______．（只填结果）
18、（10分）在数学拓展课上，老师让同学们探讨特殊四边形的做法：
如图，先作线段，作射线（为锐角），过作射线平行于，再作和的平分线分别交和于点和，连接，则四边形为菱形；
（1）你认为该作法正确吗？请说明理由.
（2）若，并且四边形的面积为，在上取一点，使得.请问图中存在这样的点吗？若存在，则求出的长；若不存在，请说明理由.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）小明参加岗位应聘中，专业知识、工作经验、仪表形象三项的得分分别为：分、分、分．若这三项的重要性之比为，则他最终得分是_________分．
20、（4分）一组数据2，x，4，6，7，已知这组数据的众数是6，那么这组数据的方差是________．
21、（4分）小明根据去年4﹣10月本班同学去电影院看电影的人数，绘制了如图所示的折线统计图，图中统计数据的中位数是______人．
22、（4分）已知反比例函数的图像过点、，则__________．
23、（4分）如图，菱形ABCD中，点O为对角线AC的三等分点且AO＝2OC，连接OB，OD，OB＝OC＝OD，已知AC＝3，那么菱形的边长为_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）(江苏省泰州市海陵区2018年中考适应性训练数学试题) 如图，直线AB：y=−x−b分别与x、y轴交于A（6，0）、B两点，过点B的直线交x轴的负半轴于点C，且OB∶OC=3∶1．
（1）求点B的坐标；
（2）求直线BC的函数关系式；
（3）若点P（m，2）在△ABC的内部，求m的取值范围．
25、（10分）如图，中，是边上一点，，，，点，分别是，边上的动点，且始终保持．

（1）求的长；
（2）若四边形为平行四边形时，求的周长；
（3）将沿它的一条边翻折，当翻折前后两个三角形组成的四边形为菱形时，求线段的长．
26、（12分）如图，四边形ABCD是平行四边形，AE平分∠BAD，交DC的延长线于点E．求证：DA=DE．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
首先过点C作CD⊥x轴于点D，过点A作AE⊥x轴于点E，易证得△AOE≌△OCD（AAS），则可得CD=OE=1，OD=AE=，继而求得答案．
【详解】
解：过点C作CD⊥x轴于点D，过点A作AE⊥x轴于点E，
则∠ODC=∠AEO=90°，
∴∠OCD+∠COD=90°，
∵四边形OABC是正方形，
∴OC=OA，∠AOC=90°，
∴∠COD+∠AOE=90°，
∴∠OCD=∠AOE，
在△AOE和△OCD中，
，
∴△AOE≌△OCD（AAS），
∴CD=OE=1，OD=AE=，
∴点C的坐标为：（-，1）．
故选：D．
本题考查了正方形的性质、全等三角形的判定与性质以及勾股定理．注意准确作出辅助线、证得△AOE≌△OCD是解题的关键．
2、B
【解析】试题解析：水涨船高是必然事件，A不正确；
守株待兔是随机事件，B正确；
水中捞月是不可能事件，C不正确
缘木求鱼是不可能事件，D不正确；
故选B．
考点：随机事件.
3、C
【解析】
先得出这个多边形的边数，再根据多边形的内角和公式即可得．
【详解】
从一个顶点出发的对角线共有3条
这个多边形是一个六边形
则这个多边形的内角和为
故选：C．
本题考查了多边形的内角和公式，正确求出多边形的边数是解题关键．
4、A
【解析】
试题分析：∵正比例函数（）的函数值y随x的增大而减小，∴k＜0，∴一次函数的图像经过二、三、四象限．故选A．
考点：一次函数的性质．
5、A
【解析】
此题可过P作PE⊥OM，过点N作NF⊥OM，根据勾股定理求出OP的长度，则N点坐标便不难求出．
【详解】
过P作PE⊥OM，过点N作NF⊥OM，
∵顶点P的坐标是（3，4），
∴OE=3，PE=4，
∵四边形ABCD是平行四边形，
∴OE=MF=3，
∵4+3=7，
∴点N的坐标为（7，4）．
故选A．
此题考查了平行四边形的性质，根据平行四边形的性质和点P的坐标，作出辅助线是解决本题的突破口．
6、C
【解析】
A、22+32≠42 ，故不是直角三角形，A不符合题意；B、（）2+（）2≠（）2 ，故不是直角三角形，B不符合题意；C、12+（ ）2=22 ，故是直角三角形，C符合题意；D、72+82≠92 ，故不是直角三角形，D不符合题意；
故选C．
7、B
【解析】
分别从3个条件中选取2个，共3种情况：若选AB∥CD，AB=CD，若选AB∥CD，AD∥BC，若选AB=CD，AD∥BC，逐一利用平行四边形的判定方法验证即可．
【详解】
若选AB∥CD，AB=CD，
∵AB∥CD，AB=CD，
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）；
若选AB∥CD，AD∥BC，
∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）；
若选AB=CD，AD∥BC，不能说明四边形ABCD是平行四边形；
故选：B．
本题主要考查平行四边形的判定，掌握平行四边形的判定方法是解题的关键．
8、D
【解析】
根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个三角形就不是直角三角形．
【详解】
A、12+22≠32，根据勾股定理的逆定理不是直角三角形，故此选项错误；
B、12+（）2≠32，根据勾股定理的逆定理不是直角三角形，故此选项错误；
C、52+62≠72，根据勾股定理的逆定理不是直角三角形，故此选项错误；
D、52+122=132，根据勾股定理的逆定理是直角三角形，故此选项正确．
故选：D．
此题考查勾股定理的逆定理，解题关键在于在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、.
【解析】
由可得，化简即可得到，再计算，即可求得=.
【详解】
∵，
∴，
∴，
∴，
∴=.
故答案为：.
本题考查了完全平方公式的变形应用，正确求得是解决问题的关键.
10、
【解析】
把a1，a2，a3代入代数式计算，找出规律，根据规律计算．
【详解】
a1=，
，
，
……，
2019÷3=673，
∴a2019=-1，
故答案为：-1．
本题考查的是规律型：数字的变化类问题，正确找出数字的变化规律是解题的关键．
11、180°
【解析】
解：∵AB∥CD
∴∠1=∠EFD
∵∠2+∠EFC=∠3
∠EFD=180°-∠EFC
∴∠1+∠3—∠2=180°
故答案为：180°
12、1
【解析】
根据一次函数的性质可得∠B1OA1=45°，然后求出△OA2B2是等腰直角三角形，△OA3B2是等腰直角三角形，然后根据等腰直角三角形斜边上的高等于斜边的一半求出OA3，同理求出OA4，然后根据变化规律写出即可．
【详解】
解：∵直线为y=x，
∴∠B1OA1=45°，
∵△A2B2A3，
∴B2A2⊥x轴，∠B2A3A2=45°，
∴△OA2B2是等腰直角三角形，△OA3B2是等腰直角三角形，
∴OA3=2A2B2=2OA2=2×2=4，
同理可求OA4=2OA3=2×4=23，
…，
所以，OA2019=1．
故答案为：1.
本题考查了一次函数图象上点的坐标特征，等腰直角三角形的性质，熟记性质并确定出等腰直角三角形是解题的关键．
13、9；9
【解析】
【分析】根据中位数和众数定义可以分析出结果.
【详解】这组数据中9出现次数最多，故众数是9；按顺序最中间是9，所以中位数是9.
故答案为9；9
【点睛】本题考核知识点：众数，中位数.解题关键点：理解众数，中位数的定义.
三、解答题（本大题共5个小题，共48分）
14、（1）6，，图见解析；（2）；（3）1．
【解析】
（1）先求出随机调查的家庭总户数，再根据“频数频率总数”可求出a的值，根据“频率频数总数”可求出b的值，然后补全频数分布直方图即可；
（2）根据总户数和频数分布表中“月均用气量不超过的家庭数”即可得；
（3）先求出“小区月均用气量超过的家庭”的占比，再乘以600即可得．
【详解】
（1）随机调查的家庭总户数为（户）
则
补全频率分布直方图如下所示：
（2）月均用气量不超过的家庭数为（户）
则
答：月均用气量不超过30的家庭数占被调查家庭总数的百分比为；
（3）小区月均用气量超过的家庭占比为
则（户）
答：该小区月均用气量超过40的家庭大约有1户．
本题考查了频数分布表和频数分布直方图，掌握理解频数分布表和频数分布直方图是解题关键．
15、（1）C；（2）否，（x﹣2）1；（3）（x2﹣2x）（x2﹣2x+2）+1＝（x﹣1）1．
【解析】
（1）根据分解因式的过程直接得出答案；
（2）该同学因式分解的结果不彻底，进而再次分解因式得出即可；
（3）将看作整体进而分解因式即可．
【详解】
（1）该同学第二步到第三步运用了因式分解的两数和的完全平方公式；
故选：C；
（2）这个结果没有分解到最后，
原式＝（x2﹣1x+1）2＝（x﹣2）1；
故答案为：否，（x﹣2）1；
（3）设为x2﹣2x＝t,
则原式=t（t+2）+1
=t2+2t+1
=（t+1）2
=（x2﹣2x+1）2
=（x﹣1）1.
此题主要考查了公式法分解因式，熟练利用完全平方公式分解因式是解题关键，注意分解因式要彻底．
16、（2）①m＝1；②﹣2020；（1）该函数的最小值为﹣2；该函数图象与x轴围成的几何图形的面积是4；（4）当y1≥y时x的取值范围是﹣1≤x≤1．
【解析】
（2）①把x＝1代入y＝|x|﹣2，即可求出m；
②把y＝2018代入y＝|x|﹣2，即可求出n；
（1）画出该函数的图象即可求解；
（4）在同一平面直角坐标系中画出函数y1＝x﹣与函数y＝|x|﹣2的图象，根据图象即可求出y1≥y时x的取值范围．
【详解】
（2）①把x＝1代入y＝|x|﹣2，得m＝1；
②把y＝2018代入y＝|x|﹣2，得2018＝|x|﹣2，
解得x＝﹣2020或2020，
∵A（n，2018），B（2020，2018）为该函数图象上不同的两点，
∴n＝﹣2020；
（1）该函数的图象如图，
由图可得，该函数的最小值为﹣2；该函数图象与x轴围成的几何图形的面积是×4×2＝4；
（4）在同一平面直角坐标系中画出函数y1＝x﹣与函数y＝|x|﹣2的图象，
由图形可知，当y1≥y时x的取值范围是﹣1≤x≤1．
故答案为：（2）①m＝1；②﹣2020；（1）该函数的最小值为﹣2；该函数图象与x轴围成的几何图形的面积是4；（4）当y1≥y时x的取值范围是﹣1≤x≤1．
本题考查了一次函数的图象与性质，一次函数图象上点的坐标特征．正确画出函数的图象，利用数形结合思想是解题的关键．
17、见解析
【解析】
试题分析：探究：由四边形ABCD、四边形CEFG均为菱形，利用SAS易证得△BCE≌△DCG，则可得BE=DG；
应用：由AD∥BC，BE=DG，可得S△ABE+S△CDE=S△BEC=S△CDG=8，又由AE=3ED，可求得△CDE的面积，继而求得答案．
试题解析：
探究：∵四边形ABCD、四边形CEFG均为菱形，
∴BC=CD，CE=CG，∠BCD=∠A，∠ECG=∠F．
∵∠A=∠F，
∴∠BCD=∠ECG．
∴∠BCD-∠ECD=∠ECG-∠ECD，
即∠BCE=∠DCG．
在△BCE和△DCG中，

∴△BCE≌△DCG（SAS），
∴BE=DG．
应用：∵四边形ABCD为菱形，
∴AD∥BC，
∵BE=DG，
∴S△ABE+S△CDE=S△BEC=S△CDG=8，
∵AE=3ED，
∴S△CDE= ,
∴S△ECG=S△CDE+S△CDG=10
∴S菱形CEFG=2S△ECG=20.
18、（1）作法正确（2）或
【解析】
（1）根据作法可以推出，又因为，所以四边形是平行四边形，又，所以四边形是菱形，因此作法正确；
（2）作，由面积公式可求出,由菱形的性质可得AD=AB=4，用勾股定理可得，由锐角三角函数得，所以是正三角形.再根据菱形对角线互相垂直的性质，利用勾股定理解得或.
【详解】
（1）作法正确.理由如下：
∵
∴
∵平分，平分
∴
∴
∴
又∵
∴四边形是平行四边形
∵
∴四边形是菱形.
故作法正确.
（2）存在.
如图，作
∵，
∴ 且
∴由勾股定理得
∴由锐角三角函数得
∴是正三角形
∴
∵ ∴
∴或
本题考查了菱形的性质和判定，勾股定理和锐角三角函数，是一个四边形的综合题.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、15.1
【解析】
根据加权平均数的计算公式列出算式，再进行计算即可得出答案．
【详解】
根据题意得：（分），
答：他最终得分是15.1分．
故答案为：15.1．
本题考查了加权平均数的概念．在本题中专业知识、工作经验、仪表形象的权重不同，因而不能简单地平均，而应将各人的各项成绩乘以权之后才能求出最后的得分．
20、3.1
【解析】
根据众数的定义先求出x的值，然后再根据方差的公式进行计算即可得．
【详解】
解：已知一组数据1，x，4，6，7的众数是6，说明x=6，
则平均数=（1+6+4+6+7）÷5=15÷5=5，
则这组数据的方差==3.1，
故答案为3.1．
本题考查了众数、方差等，熟练掌握众数的定义、方差的计算公式是解题的关键．
21、1
【解析】
将这7个数按大小顺序排列，找到最中间的数即为中位数．
【详解】
解：这组数据从大到小为：27，1，1，1，42，42，46，
故这组数据的中位数1．
故答案为1．
此题考查了折线统计图及中位数的知识，关键是掌握寻找中位数的方法，一定不要忘记将所有数据从小到大依此排列再计算，难度一般．
22、
【解析】
根据反比例函数的增减性，结合点A和点B的横坐标的大小，即可得到答案．
【详解】
∵m2≥0，
∴m2+2＞m2+1，
∵反比例函数y=，k＞0，
∴当x＞0时，y随着x的增大而减小，
∴y1＞y2，
故答案为：＞．
本题考查了反比例函数图象上点的坐标特征，正确掌握反比例函数的增减性是解题的关键．
23、.
【解析】
如图，连接BD交AC于E，由四边形ABCD是菱形，推出AC⊥BD，AE=EC，在Rt△EOD中，利用勾股定理求出DE，在Rt△ADE中利用勾股定理求出AD即可．
【详解】
如图，连接BD交AC于E．
∵四边形ABCD是菱形，
∴AC⊥BD，AE＝EC，
∵OA＝2OC，AC＝3，
∴CO＝DO＝2EO＝1，AE＝，
∴EO＝，DE＝EB＝，
∴AD＝．
故答案为．
本题考查菱形的性质、勾股定理等知识，解题的关键是灵活应用勾股定理解决问题.
二、解答题（本大题共3个小题，共30分）
24、（1）（0，6）；（2）y=3x+6；（3）−