北京市怀柔区九级2024-2025学年九上数学开学经典模拟试题【含答案】

这是一份北京市怀柔区九级2024-2025学年九上数学开学经典模拟试题【含答案】，共22页。试卷主要包含了选择题，四象限B．第一，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）若一元二次方程有实数根，则实数的取值范围是( )
A．B．C．D．
2、（4分）一个多边形的内角和是7200，则这个多边形的边数是( )
A．2B．4C．6D．8
3、（4分）一条直线y=kx+b，其中k+b=﹣5、kb=6，那么该直线经过
A．第二、四象限B．第一、二、三象限C．第一、三象限D．第二、三、四象限
4、（4分）若，则的值为（ ）
A．B．C．D．
5、（4分）已知a＞b，若c是任意实数，则下列不等式中总是成立的是（）
A．a-c＞b-cB．a+c＜b+cC．ac＞bcD．ac＜bc
6、（4分）如图，是我国古代数学家在为《周髀算经》作注解时给出的“弦图”，给出“弦图”的这位数学家是（ ）
A．毕达哥拉斯B．祖冲之C．华罗庚D．赵爽
7、（4分）若函数有意义，则
A． B． C． D．
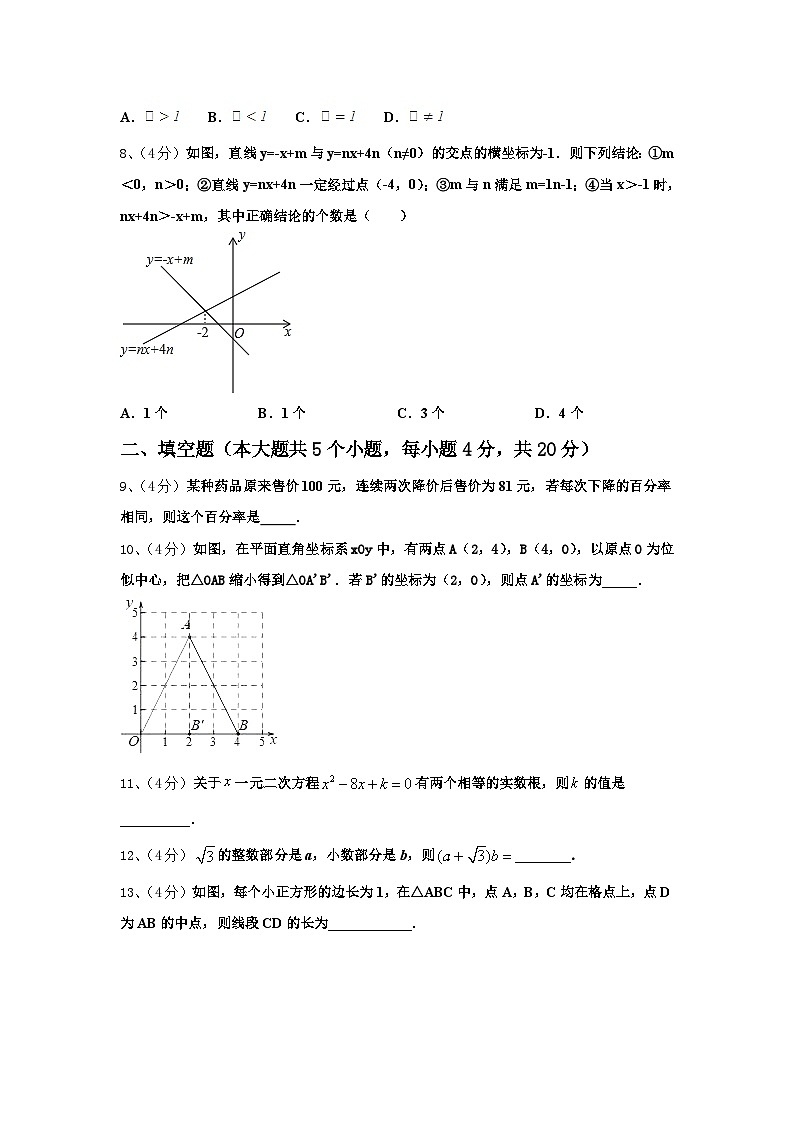
8、（4分）如图，直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-1．则下列结论：①m＜0，n＞0；②直线y=nx+4n一定经过点（-4，0）；③m与n满足m=1n-1；④当x＞-1时，nx+4n＞-x+m，其中正确结论的个数是（ ）
A．1个B．1个C．3个D．4个
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）某种药品原来售价100元，连续两次降价后售价为81元，若每次下降的百分率相同，则这个百分率是 ．
10、（4分）如图，在平面直角坐标系xOy中，有两点A（2，4），B（4，0），以原点O为位似中心，把△OAB缩小得到△OA'B'．若B'的坐标为（2，0），则点A'的坐标为_____．
11、（4分）关于一元二次方程有两个相等的实数根，则的值是__________．
12、（4分）的整数部分是a，小数部分是b，则________.
13、（4分）如图，每个小正方形的边长为1，在△ABC中，点A，B，C均在格点上，点D为AB的中点，则线段CD的长为____________.
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，矩形中，，，为上一点，将沿翻折至，与相交于点，与相交于点，且．
（1）求证：；
（2）求的长度．
15、（8分）在矩形ABCD中，AB＝4，AD＝3，矩形内部有一动点P满足S矩形ABCD＝3S△PAB，则PA+PB的最小值为_____．
16、（8分）如图，矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1．
（1）断⊿BEC的形状，并说明理由；
（2）判断四边形EFPH是什么特殊四边形？并证明你的判断．
17、（10分）计算: （1）； (2).
18、（10分）如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且∠BEF＝90°，延长EF交BC的延长线于点G；
(1)求证：△ABE∽△EGB；
(2)若AB＝4，求CG的长.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，如果一次函数与反比例函数的图象交于，两点，那么不等式的解为________.
20、（4分）如图，将平行四边形ABCD沿对角线BD折叠，使点A落在点处若，则为______ ．
21、（4分）如图，点C为线段AB上一点，且CB＝1，分别以AC、BC为边，在AB的同一侧作等边△ACD和等边△CBE，连接DE，AE，∠CDE＝30°，则△ADE的面积为_____．
22、（4分）函数，当时，_____；当1＜＜2时，随的增大而_____（填写“增大”或“减小”）.
23、（4分）在平面直角坐标系xOy中，直线与x，y轴分别交于点A，B，若将该直线向右平移5个单位，线段AB扫过区域的边界恰好为菱形，则k的值为_____.
二、解答题（本大题共3个小题，共30分）
24、（8分）四川苍溪小王家今年红心猕猴桃喜获丰收，采摘上市20天全部销售完，小王对销售情况进行跟踪记录，并将记录情况绘制成图象，日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图（1）所示，红星猕猴桃的价格z（单位：元/千克）与上市时间x（天）的函数关系式如图（2）所示．
（1）观察图象，直接写出日销售量的最大值；
（2）求小王家红心猕猴桃的日销量y与上市时间x的函数解析式；并写出自变量的取值范围．
（3）试比较第6天和第13天的销售金额哪天多？
25、（10分）在▱ABCD中，点E为AB边的中点，连接CE，将△BCE沿着CE翻折，点B落在点G处，连接AG并延长，交CD于F．
（1）求证：四边形AECF是平行四边形；
（2）若CF＝5，△GCE的周长为20，求四边形ABCF的周长．
26、（12分）如图，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，过点A作AE⊥CD于点F，交CB于点E，且∠EAB＝∠DCB．
（1）求∠B的度数：
（2）求证：BC＝3CE．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
由一元二次方程根的判别式△≥0，结合一元二次方程的定义，即可求出k的取值范围．
【详解】
解：由题意得：，
，，
∴解得：．
故选：D.
本题考查了一元二次方程根的判别式，以及一元二次方程的定义，解题的关键是熟练掌握根的判别式求参数的取值范围.
2、C
【解析】
n边形的内角和为（n-2）180°，由此列方程求n的值
【详解】
解：设这个多边形的边数是n，
则：（n-2）180°=720°，
解得n=6，
故选：C．
本题考查根据多边形的内角和计算公式求多边形的边数，解答时要会根据公式进行正确运算、变形和数据处理．
3、D
【解析】
∵k＋b=－5，kb=6，∴kb是一元二次方程的两个根．
解得，或．∴k＜1，b＜1．
一次函数的图象有四种情况：
①当，时，函数的图象经过第一、二、三象限；
②当，时，函数的图象经过第一、三、四象限；
③当，时，函数的图象经过第一、二、四象限；
④当，时，函数的图象经过第二、三、四象限．
∴直线y=kx+b经过二、三、四象限．故选D．
4、C
【解析】
首先设，将代数式化为含有同类项的代数式，即可得解.
【详解】
设
∴
∴
故答案为C.
此题主要考查分式计算，关键是设参数求值.
5、A
【解析】
根据不等式的性质，应用排除法分别将各选项分析求解即可求得答案.
【详解】
A、∵a＞b，c是任意实数，∴a-c＞b-c，故本选项正确；
B、∵a＞b，c是任意实数，∴a+c＞b+c，故本选项错误；
C、当a＞b，c＜0时，ac＞bc，而此题c是任意实数，故本选项错误；
D、当a＞b，c＞0时，ac＜bc，而此题c是任意实数，故本选项错误．
故选A.
6、D
【解析】
我国三国时期数学家赵爽为了证明勾股定理，创造了一幅“弦图”，后人称其为“赵爽弦图”，“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲.
【详解】
解：我国三国时期数学家赵爽在为《周髀算经》作注解时创造了一幅“弦图”，后人称其为“赵爽弦图”， “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲.
故答案是：D.
本题考查了学生对我国数学史的了解，籍此培养学生的爱国情怀和民族自豪感，增强学习数学的兴趣.
7、D
【解析】
解：由题意得：x﹣1≠0，解得x≠1．故选D．
8、D
【解析】
①由直线y=-x+m与y轴交于负半轴，可得m＜0；y=nx+4n（n≠0）的图象从左往右逐渐上升，可得n＞0，即可判断结论①正确；
②将x=-4代入y=nx+4n，求出y=0，即可判断结论②正确；
③由整理即可判断结论③正确；
④观察函数图象，可知当x＞-1时，直线y=nx+4n在直线y=-x+m的上方，即nx+4n＞-x+m，即可判断结论④正确．
【详解】
解：①∵直线y=-x+m与y轴交于负半轴，∴m＜0；
∵y=nx+4n（n≠0）的图象从左往右逐渐上升，∴n＞0，
故结论①正确；
②将x=-4代入y=nx+4n，得y=-4n+4n=0，
∴直线y=nx+4n一定经过点（-4，0）．
故结论②正确；
③∵直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-1，
∴当x=-1时，y=1+m=-1n+4n，
∴m=1n-1．
故结论③正确；
④∵当x＞-1时，直线y=nx+4n在直线y=-x+m的上方，
∴当x＞-1时，nx+4n＞-x+m，
故结论④正确．
故选：D．
本题考查了一次函数图象上点的坐标特征、一次函数与一元一次不等式以及一次函数的图象，逐一分析四条结论的正误是解题的关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、10%．
【解析】
设平均每次降价的百分率为，那么第一次降价后的售价是原来的，那么第二次降价后的售价是原来的，根据题意列方程解答即可.
【详解】
设平均每次降价的百分率为，根据题意列方程得，
，
解得，（不符合题意，舍去），
答：这个百分率是.
故答案为.
本题考查一元二次方程的应用，要掌握求平均变化率的方法.若设变化前的量为，变化后的量为，平均变化率为，则经过两次变化后的数量关系为.
10、（1，2）
【解析】
根据位似变换的性质，坐标与图形性质计算．
【详解】
点B的坐标为（4，0），以原点O为位似中心，把△OAB缩小得到△OA'B'，B'的坐标为（2，0），
∴以原点O为位似中心，把△OAB缩小，得到△OA'B'，
∵点A的坐标为（2，4），
∴点A'的坐标为（2×，4×），即（1，2），
故答案是：（1，2）．
考查的是位似变换，坐标与图形性质，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．
11、16
【解析】
根据根判别式得出答案.
【详解】
因为关于一元二次方程有两个相等的实数根，
所以
解得k=16
故答案为：16
考核知识点：根判别式.理解根判别式的意义是关键.
12、2
【解析】
因为1＜＜2，由此得到的整数部分a，再进一步表示出其小数部分b．
【详解】
因为1