福建省福州第一中学2024-2025学年上学期九年级10月月考数学试题(无答案)

这是一份福建省福州第一中学2024-2025学年上学期九年级10月月考数学试题(无答案)，共5页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

班级：____________ 姓名：____________ 座号：____________
一、单选题
1．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
2．下列方程中，属于一元二次方程的是（ ）
A．B．C．D．
3．如图，在中，，则等于（ ）
A．30°B．60°C．120°D．150°
4．已知点和点关于原点对称，则（ ）
A．1B．C．3D．
5．抛物线的对称轴是（ ）
A．直线B．直线C．直线D．轴
6．将抛物线先向左平移4个单位长度，再向上平移5个单位长度，得到的函数表达式为（ ）
A．B．
C．D．
7．某工厂2022年全年某产品的产量为234万吨，预计2024年全年该产品的产量为345万吨，设2022年至2024年该产品的年平均增长率为，根据题意列出方程为（ ）
A．B．
C．D．
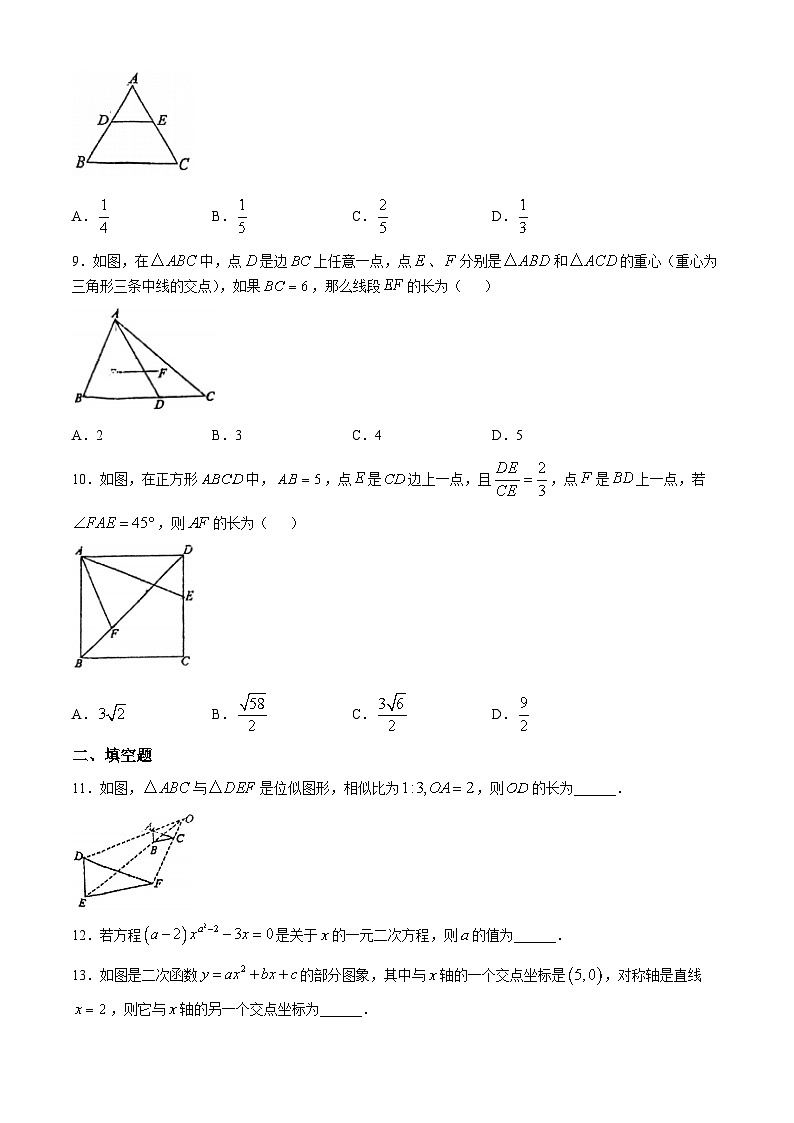
8．如图，在中，，则的值是（ ）
A．B．C．D．
9．如图，在中，点是边上任意一点，点、分别是和的重心（重心为三角形三条中线的交点），如果，那么线段的长为（ ）
A．2B．3C．4D．5
10．如图，在正方形中，，点是边上一点，且，点是上一点，若，则的长为（ ）
A．B．C．D．
二、填空题
11．如图，与是位似图形，相似比为，则的长为______．
12．若方程是关于的一元二次方程，则的值为______．
13．如图是二次函数的部分图象，其中与轴的一个交点坐标是，对称轴是直线，则它与轴的另一个交点坐标为______．
14．如图，四边形内接于，过点作，交于点．若，则等于______度．
15．方程的解是，现在给出另一个方程，它的解是______．
16．如图，已知抛物线，抛物线与轴从左到右分别交于、．点在抛物线的对称轴上，点为抛物线上位于第四象限一点，满足．点在抛物线上，且满足，则点的坐标为______．
三、解答题
17．解下列方程：
（1）；
（2）．
18．如图，在等边中，为边上一点，为边上一点，且．求证：．
19．关于的一元二次方程．
（1）试判断该方程根的情况；
（2）若是该方程的两个实数根，且，求的值．
20．如图，是的弦，点是的中点，连接并反向延长交于点．若，求的半径．
21．如图，已知的直径为，点在圆周上（异于），．
（1）若，求的长；
（2）若是的平分线，求证：直线是的切线．
22．某地今年种植12万千克的莲藕，计划在甲、乙两店销售，其中在乙店的销售量为（万千克），销售情况如下表：
（1）若在甲店销售莲藕2万千克，求销售完这批莲藕的获利总数；
（2）若该地销售完所有莲藕后，共获利28.8万元，求的值．
23．阅读与思考
请阅读以下材料并完成相应的任务．
（1）任务一：用尺规完成材料中的作图，保留作图痕迹，并标明字母．
（2）任务二：请你完成引理结论的证明过程．
24．如图1，为的直径，是上异于的任一点，连接，过点作射线为射线上一点，连接．
（1）若点在直线同侧，且，求证：四边形是平行四边形；
（2）若在点运动过程中，始终有，连接．
①如图2，时，求的长度；
②求长度的取值范围．
25．如图，抛物线与轴交于两点，与轴交于点，对称轴直线．
（1）求抛物线解析式；
（2）如图1，直线与抛物线，轴分别交于点于点，点在坐标平面内，若，求点的纵坐标；
（3）如图2，若过（2）中点的直线与抛物线交于两点（点在点左侧），过点的直线与抛物线交于点，探究直线是否经过某个定点？若经过某定点，求该定点的坐标；若不经过定点，请说明理由．甲店
乙店
利润（万元/万千克）
2
伟大的古希腊数学家、哲学家、物理学家阿基米德提出了有关圆的一个引理．这个引理的作图步骤如下：
①如图，已知是弦上一点，作线段的垂直平分线，分别交于点于点，连接．
②以点为圆心，的长为半径作弧，交于点（两点不重合），连接．
引理的结论：．