

河南省信阳市息县2024届九年级下学期中考适应性测试(四)数学试卷(含解析)
展开一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个数中,绝对值最大的是( )
A. 2B. -13C. 0D. -3
2.2024年4月25号,我国神舟十八号载人飞船发射取得圆满成功,在发射过程中,飞船的速度约为每小时29000千米,数据29000用科学记数法表示为( )
A. 2.9×106B. 2.9×105C. 2.9×104D. 29×103
3.中国古代数学名著《九章算术注》中记载:“邪解立方,得两堑堵.”意即把一长方体沿对角面一分为二,这相同的两块叫做“堑堵”.如图是“堑堵”的立体图形,它的左视图为( )
A. B. C. D.
4.下列计算正确的是( )
A. a4⋅a2=a8B. a6÷a3=a2C. a2=aD. (-3a3)2=9a6
5.如图,直线a//b,直角三角形如图放置,∠DCB=90°,若∠1=118°,则∠2的度数为( )
A. 28°
B. 38°
C. 26°
D. 30°
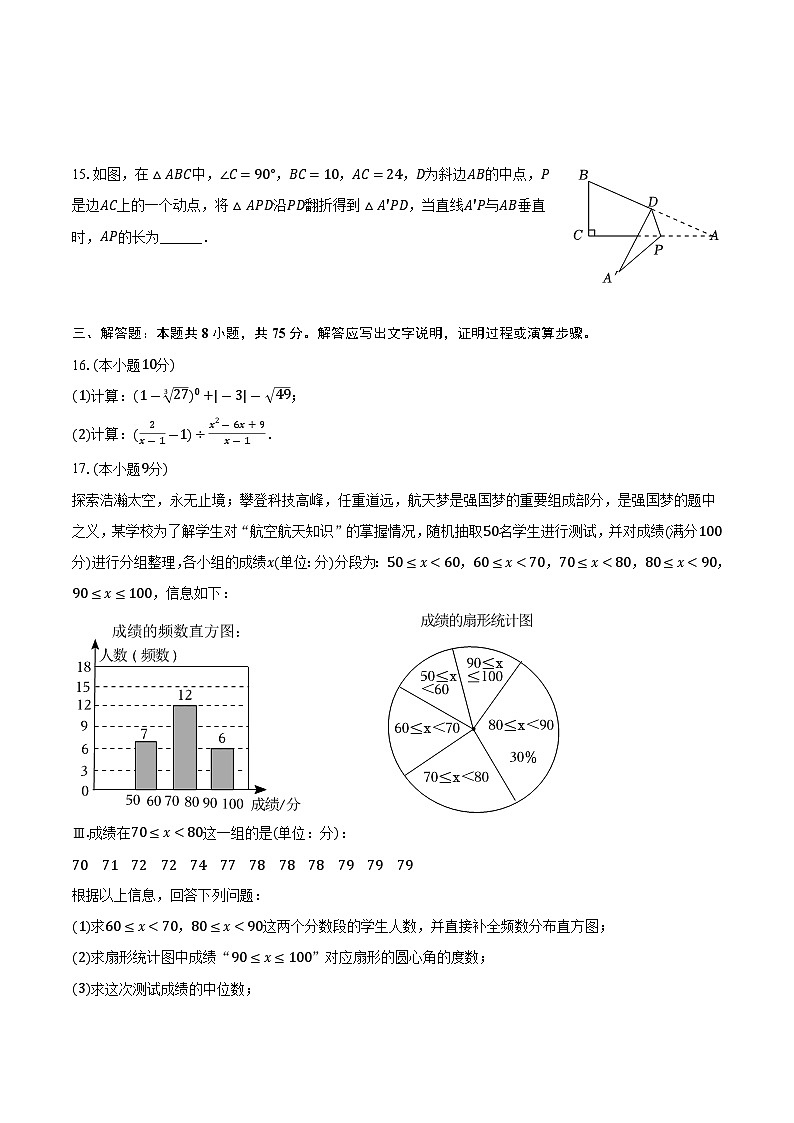
6.若关于x的方程x2-x+m=0没有实数根,则m的值可以为( )
A. -1B. 14C. 0D. 1
7.如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=25°,则∠BDC=( )
A. 85°
B. 75°
C. 70°
D. 65°
8.杠杆原理也称为“杠杆平衡条件”,要使杠杆平衡,作用在杠杆上的两个力矩(力与力臂的乘积)大小必须相等,即F1×L1=F2×L2.如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,右侧力F与力臂L满足的函数关系是( )
A. 正比例函数关系B. 一次函数关系C. 反比例函数关系D. 二次函数关系
9.图为一把椅子的侧面示意图,已知DE//地面AB,DE=20cm,CB=2CE,CA=45CB,则地面上AB两点之间的距离为( )
A. 30cm
B. 32cm
C. 34cm
D. 36cm
10.如图1,点D在△ABC边AC上,点E是BD上的一动点,点F是CE的中点,连接AF,设BE=x,AF=y,图2是点E运动时y随x变化的关系图象,其中点H是函数图象的最低点,则n的值为( )
A. 24B. 26C. 28D. 30
二、填空题:本题共5小题,每小题3分,共15分。
11.4的平方根是______.
12.在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有______个.
13.不等式组3-x2≤13x+2≥1的解集是______.
14.如图,正方形ABCD的边长为1,对角线AC,BD相交于点O,以点B为圆心,对角线BD的长为半径画弧,交BC的延长线于点E,则图中阴影部分的面积为______.
15.如图,在△ABC中,∠C=90°,BC=10,AC=24,D为斜边AB的中点,P是边AC上的一个动点,将△APD沿PD翻折得到△A'PD,当直线A'P与AB垂直时,AP的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
(1)计算:(1-327)0+|-3|- 49;
(2)计算:(2x-1-1)÷x2-6x+9x-1.
17.(本小题9分)
探索浩瀚太空,永无止境;攀登科技高峰,任重道远,航天梦是强国梦的重要组成部分,是强国梦的题中之义,某学校为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(满分100分)进行分组整理,各小组的成绩x(单位:分)分段为:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100,信息如下:
Ⅲ.成绩在70≤x<80这一组的是(单位:分):
70ㅤ71ㅤ72ㅤ72ㅤ74ㅤ77ㅤ78ㅤ78ㅤ78ㅤ79ㅤ79ㅤ79
根据以上信息,回答下列问题:
(1)求60≤x<70,80≤x<90这两个分数段的学生人数,并直接补全频数分布直方图;
(2)求扇形统计图中成绩“90≤x≤100”对应扇形的圆心角的度数;
(3)求这次测试成绩的中位数;
(4)这次测试成绩的平均数是76.4分,甲的测试成绩是77分,乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩”你认为乙的说法正确吗?请说明理由.
18.(本小题9分)
如图,△ABC中,∠B=2∠C.
(1)请完成尺规作图:过点A作AD⊥BC,垂足为D.
(要求:不写作法,保留作图痕迹.)
(2)在(1)的基础上,求证:DC=AB+BD.
19.(本小题9分)
如图,将直线y=-x向上平移5个单位长度后得到直线y1,直线y1与反比例函数y2=mx(m≠0)在第一象限的图象交于点A(2,3)和点B.直线y1与x轴交于点M.
(1)求点B的坐标;
(2)在x轴上取一点N,当△AMN的面积为6时,求点N的坐标;
20.(本小题9分)
某“综合与实践”小组开展测量某建筑物AB高度的活动.他们制订了测量方案,
参考数据结果精确到0.1米,参考数据: 5=2.236.请根据以上测量结果,求AB的长.
21.(本小题9分)
某班计划从商店购买图书和文具盒,已知购买一本图书比购买一个文具盒多用5元,若用400元购买图书,用160元购买文具盒,且购买文具盒的个数是购买图书本数的一半.
(1)购买一本图书和一个文具盒各需要多少元?
(2)如果该班需要图书数量是文具盒数量的2倍还少2,且该班购买图书和文具盒的总费用不超过720元,那么该班最多可购买多少本图书?
22.(本小题10分)
如图1,一灌溉车正为绿化带浇水,喷水口H离地竖直高度为h=1.2米.建立如图2所示的平面直角坐标系,可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象,把绿化带横截面抽象为矩形DEFG,其水平宽度DE=2米,竖直高度EF=0.7米,下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2米,高出喷水口0.4米,灌溉车到绿化带的距离OD为d米.
(1)求上边缘抛物线喷出水的最大射程OC;
(2)求下边缘抛物线与x轴交点B的坐标;
(3)若d=3.2米,通过计算说明灌溉车行驶时喷出的水能否浇灌到整个绿化带.
23.(本小题10分)
综合与实践
【问题背景】
如图1,在矩形ABCD中,AB=5,BC=4,点E为边BC上一点,沿直线DE将矩形折叠,使点C落在AB边上的点C'处.
【问题解决】
(1)填空:AC'的长为______;
(2)如图2,展开后,将△DC'E沿线段AB向右平移,使点C'的对应点与点B重合,得到△D'BE',D'E'与BC交于点F,求线段EF的长.
【拓展探究】
(3)如图1,将△DC'E绕点C'旋转至A,C',E三点共线时,请直接写出CD的长.
答案和解析
1.【答案】D
解析:解:A、|2|=2;B、|-13|=13;C、|0|=0;D、|-3|=3;
∵0<13<2<3,
∴四个数中绝对值最大的是-3.
故选:D.
分别计算出四个选项的绝对值,然后再进行比较,找出绝对值最大的选项.
绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
2.【答案】C
解析:解:29000=2.9×104.
故选:C.
用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可
此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
3.【答案】C
解析:解:这个“堑堵”的左视图如下:
.
故选:C.
找到从几何体的左面看所得到的图形即可.
本题考查了简单几何体的三视图,注意主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
4.【答案】D
解析:解:由题意可得,a4⋅a2=a6,计算错误,故A不符合题意;
a6÷a3=a3,计算错误,故B不符合题意;
a2=|a|,计算错误,故C不符合题意;
(-3a3)2=9a6,计算正确,故D符合题意;
故选:D.
根据根式的性质及同底数幂乘除法法则直接逐个判断即可得到答案.
本题考查了根式的性质及同底数幂乘除法法则,掌握(am)n=amn,am⋅an=am+n,am÷an=am-n是关键.
5.【答案】A
解析:解:如图,
∵a//b,∠1=118°,
∴∠BCE=∠1=118°,
∵∠DCB=90°,
∴∠2=∠BCE-∠DCB=28°.
故选:A.
由平行线的性质可求得∠ACE=118°,从而可求∠2的度数.
本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,同位角相等.
6.【答案】D
解析:解:∵关于x的方程x2-x+m=0没有实数根,
∴Δ=(-1)2-4×1×m=1-4m<0,
解得:m>14.
故选:D.
根据关于x的方程x2-x+m=0没有实数根,得到Δ<0,求出m的取值范围,再找出符合条件的m的值即可.
本题主要考查了一元二次方程根的判别式,掌握一元二次方程没有实数根它的判别式小于零是解决问题的关键.
7.【答案】D
解析:解:连接OC,如图,
∵∠ABC=25°,
∴∠AOC=2∠ABC=2×25°=50°,
∴∠BOC=180°-∠AOC=180°-50°=130°,
∴∠BDC=12∠BOC=12×130°=65°.
故选:D.
连接OC,根据圆周角定理可得∠AOC的度数,再根据平角的性质可得∠BOC的度数,再根据圆周角定理即可求出∠BDC的度数.
本题主要考查了圆周角定理,熟练应用圆周角定理进行求解是解决本题的关键.
8.【答案】C
解析:解:∵保证杠杆水平平衡的条件,
∴F1×L1=F2×L2,
∵铁架台左侧钩码的个数与位置都不变,
∴F1×L1为常数,
∴右侧力F与力臂L满足的函数关系是反比例函数关系,
故选:C.
根据F1×L1=F2×L2以及铁架台左侧钩码的个数与位置都不变即可得到结论.
本题考查了反比例函数的应用,正确理解题意是解题的关键.
9.【答案】B
解析:解:∵CB=2CE,CA=45CB,
∴CECA=12CB45CB=58.
∵DE//地面AB,
∴△DEC∽△BAC,
∴DEAB=CECA=58,
又∵DE=20cm,
∴AB=32cm,
故选:B.
由题意得出CE与CA的比值,再根据相似三角形的判定与性质得到DEAB=CECA=58,即可得出结果.
本题考查了相似三角形应用,熟记相似三角形的判定与性质是解题的关键.
10.【答案】C
解析:解:如图,
设M为BC的中点,N为CD的中点,连接AM,MN,可知F的运动轨迹为MN,
根据图象的第一个点(0,13)可知E在B点时F与BC的中点M重合,即AM=13;
由图象最后一个点可知E与D重合时,F与CD的中点N重合,AN=15;
当AF⊥MN的时候,AF最小为12,
在Rt△AMF和Rt△ANF中,根据勾股定理得,
MF= AM2-AF2= 132-122=5,NF= AN2-AF2= 152-122=9,
∴BD=2MN=2×(5+9)=28,
∴n=28.
故选:C.
根据图象的第一个点(0,13)可知E在B点时F为BC的中点,所以BC边的中线长AM为13;由图象最后一个点可知E与D重合时,F为CD的中点,AN=15;因为F为EC的中点,可知F的运动轨迹是△BCD的中位线MN,所以当AF垂直于中位线的时候AF最小为12,根据勾股定理求出中位线即可得BD即n的值.
本题考查的是动点图象问题,涉及到动点的轨迹问题、中位线定理和勾股定理的运用等知识,此类问题关键是:弄清楚所给点的坐标的意义,图象和图形的对应关系,进而求解.
11.【答案】±2
解析:解:∵(±2)2=4,
∴4的平方根为±2,
故答案为±2.
12.【答案】14
解析:解:由题意可得,
总的可能有:6÷30%=20,20-6=14,
故答案为:14.
根据概率公式P(n)=nm求出总数,利用总数减去白球的即可得到答案.
本题考查求简单概率,解题的关键是熟练掌握概率公式P(n)=nm.
13.【答案】x≥1
解析:解:解不等式3-x2≤1,得:x≥1,
解不等式3x+2≥1,得:x≥-13,
∴不等式组的解集为x≥1.
故答案为:x≥1.
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
14.【答案】π4
解析:解:∵四边形ABCD是正方形,
∴∠BCD=90°,∠DBC=45°,
∵AB=1,
∴BC=1,BD= 2,
∴阴影部分的面积:S=S扇形BDE=45π×( 2)2360=π4,
故答案为:π4.
先根据锐角三角函数求出BD,再根据扇形面积公式和三角形面积公式即可求出阴影部分的面积.
本题考查有关扇形面积的相关计算、正方形的性质,掌握扇形面积公式和矩形的性质的应用,其中根据锐角三角函数求出BC、BD是解题关键.
15.【答案】263或392
解析:解:①A在AC下方时,如图1:
延长AP交AB于点H,则AH⊥AB,AD=AD,∠A=∠A,
∵∠C=90°,BC=10,AC=24,D为斜边AB的中点,
∴AB= AC2+BC2=26,
∴AD=AD=2AB=13,csA=ACAB=1213,sinA=sinA'=BCAB=513,
∴sinA'=DHA'D=513,
解得:DH=5,
∴AH=AD-DH=8,
∴csA=AHAP=1213,
解得:AP=263;
②A在AB上方时,如图2:
同理可得:DH=5,
∴AH=AD+DH=18,
∴csA=AHAP=1213,
解得:AP=392,
综上所述:AP=263或AP=392,
故答案为:263或392.
根据题意分类讨论①A在AC下方、②A在AB上方两种情况,即可求解.
本题考查翻折变换(折叠问题),解直角三角形等知识点,熟练掌握轴对称的性质,直角三角形的性质,勾股定理是解题的关键.
16.【答案】解:(1)(1-327)0+|-3|- 49
=1+3-7
=-3;
(2)(2x-1-1)÷x2-6x+9x-1
=2-(x-1)x-1⋅x-1(x-3)2
=3-xx-1⋅x-1(x-3)2
=13-x.
解析:(1)先化简各式,然后再进行计算即可解答;
(2)先利用异分母分式加减法法则计算括号里,再算括号外,即可解答.
本题考查了分式的混合运算,实数的运算,零指数幂,准确熟练地进行计算是解题的关键.
17.【答案】解:(1)80≤x<90分数段的学生人数为50×30%=15(人),
60≤x<70分数段的学生人数为50-7-12-15-6=10(人).
补全频数分布直方图如图所示.
(2)扇形统计图中成绩“90≤x≤100”对应扇形的圆心角的度数为360°×650=43.2°.
(3)将50名学生的测试成绩按照从小到大的顺序排列,排在第25和26的成绩为78,78,
∴这次测试成绩的中位数为78+782=78(分).
(4)不正确.
理由:∵甲的成绩77分低于中位数78分,
∴甲的成绩不可能高于一半学生的成绩.
解析:(1)用50乘以扇形统计图中80≤x<90分数段的百分比可得80≤x<90分数段的学生人数.用50分别减去50≤x<60,70≤x<80,80≤x<90,90≤x≤100分数段的学生人数,可得60≤x<70分数段的学生人数.直接补全频数分布直方图即可.
(2)用360°乘以90≤x≤100分数段的学生人数所占的百分比,即可得出答案.
(3)根据中位数的定义可得答案.
(4)根据中位数的意义可得结论.
本题考查频数(率)分布直方图、扇形统计图、中位数,能够读懂统计图,掌握中位数的定义以及意义是解答本题的关键.
18.【答案】(1)解:如图,AD为所作;
(2)证明:在DC上截取DE=BD,连接AE,
∵AD⊥BE,DB=DE,
即AD垂直平分BE,
∴AE=AB,
∴∠AEB=∠B,
∵∠AEB=∠C+∠EAC,∠B=2∠C,
∴∠C=∠EAC,
∴AE=CE,
∴CD=CE+DE=AE+BD=AB+BD.
解析:(1)利用基本作图,过A点作BC的垂线即可;
(2)在DC上截取DE=BD,连接AE,则AD垂直平分BE,所以AE=AB,则∠AEB=∠B,接着证明∠C=∠EAC得到AE=CE,然后利用等线段代换得到CD=AB+BD.
本题考查了作图-复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等腰三角形的判定与性质.
19.【答案】解:(1)∵将直线y=-x向上平移5个单位长度后得到直线y1,
∴直线y1解析式为y1=-x+5,
把A(2,3)代入y2=mx(m≠0)中,m=2×3=6,
∴反比例函数解析式为y2=6x,
联立y2=6xy1=-x+5,
解得x=2y=3或x=3y=2,
∴点B的坐标为(3,2);
(2)在y1=-x+5中,当y1=-x+5=0时,x=5,
∴M(5,0),
设N(a,0),则MN=|a-5|,
∵△AMN的面积为6
∴S△AMN=12|5-a|⋅3=6,
∴|5-a|=4,
∴a=9或1
∴N(9,0)或(1,0).
解析:(1)先根据平移方式得到直线y1解析式为y1=-x+5,再把点A坐标代入反比例函数解析式中求出反比例函数解析式,再利用直线y1解析式和反比例函数解析式求出点B的坐标即可;
(2)先求出点M的坐标,设N(a,0),则MN=|a-5|,再根据三角形面积计算公式列出方程求解即可.
本题主要考查了一次函数与反比例函数,解题的关键是掌握相关知识的灵活运用.
20.【答案】解:如图,过点E作EG⊥AB,垂足为G,延长AB交DC于点H,
由题意可知:AH⊥DH,
∴四边形GHDE是矩形,
∴EG=DH,ED=GH=17米,∠FAE=45°,AF//EG,
∴∠FAE=∠AEG=45°,
∵梯形坡度i=2: 5,
∴BHCH=2 5,
∴设BH=2x米,则CH= 5x米,
在Rt△RCH中BC= BH2+CH2= (2y)2+( 5x)2=3x(米),
∴3x=9,
解得x=3,
∴BH=6米,CH=3 5米,
∵DC=20米,
∴EG=DH=CH+DC=(20+3 5)米,
在Rt△AEG中,AG=EG⋅tan45°=(20+3 5)米,
∵GH=ED=17米,
∴AB=AG+GH-BH=20+3 5+17-6=37.7米).
答:AB的长约为37.7米.
解析:过点E作EG⊥AB,垂足为G,延长AB交DC于点H,根据特殊角三角函数和勾股定理即可解决问题.
本题考查了解直角三角形的应用-仰角俯角问题,坡度坡角问题,解决本题的关键是掌握仰角俯角定义.
21.【答案】解:(1)设购买一本图书需要x元,则购买一个文具盒需要(x-5)元,则:
160x-5=12×400x.
解得x=25.
经检验:x=25是所列方程的解.
则x-5=20.
答:购买一本图书需要25元,则购买一个文具盒需要20元;
(2)设该班可购买a个文具盒,则购买图书数量为(2a-2)本,则:
20a+25(2a-2)≤720.
解得a≤11.
则2a-2≤20.
答:该班最多可购买20本图书.
解析:(1)设购买一本图书需要x元,则购买一个文具盒需要(x-5)元;根据“购买文具盒的个数=12×购买图书本数”列出方程并解答;
(2)设该班可购买a个文具盒,则购买图书数量为(2a-2)本,根据“该班购买图书和文具盒的总费用不超过720元”列出不等式并解答即可.
此题考查分式方程的实际运用,一元一次不等式的实际运用,找出题目蕴含的等量关系和不等关系是解决问题的关键.
22.【答案】解:(1)如图2,由题意得A(2,1.6)是上边缘抛物线的顶点,
设y=a(x-2)2+1.6,
又∵抛物线过点(0,1.2),
∴1.2=4a+1.6,
∴a=-110,
∴上边缘抛物线的函数解析式为y=-110(x-2)2+1.6,
当y=0时,0=-110(x-2)2+1.6,
解得x1=6,x2=-2(舍去),
∴喷出水的最大射程OC为6m;
(2)∵对称轴为直线x=2,
∴点(0,1.2)的对称点为(4,1.2),
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的,
∴点B的坐标为(2,0);
(3)∵OD=d=3.2米,DE=2米,EF=0.7米,
∴点F的坐标为(5.2,0.7),
当x=5.2时,y=-110(5.2-2)2+1.6=72125=0.576<0.7,
当x>2时,y随x的增大而减小,
∴灌溉车行驶时喷出的水不能浇灌到整个绿化带.
解析:(1)由顶点A(2,1.6)得,设y=a(x-2)2+1.6,再根据抛物线过点(0,1.2),可得a的值,从而解决问题;
(2)由对称轴知点(0,1.2)的对称点为(4,1.2),则下边缘抛物线是由上边缘抛物线向左平移4cm得到的,可得点B的坐标;
(3)根据OD=d=3.2米,DE=2米,EF=0.7米,可求得点F的坐标为(5.2,0.7),当x=5.2时,y=-110(5.2-2)2+1.6=72125=0.576<0.7,从而得出答案.
本题考查二次函数的实际应用,掌握待定系数法求二次函数解析式,二次函数的性质,二次函数与方程的关系等知识,读懂题意,建立二次函数模型是解题的关键.
23.【答案】3
解析:解:(1)∵四边形ABCD是矩形,
∴∠A=∠B=90°,AB=CD=5,BC=AD=4,
由折叠的性质得:C'D=CD=5,
∴AC'= C'D2-AD2= 52-42=3,
故答案为:3;
(2)由(1)得:AC'=3,
∴BC'=BC-AC'=2,
由折叠的性质得:C'E=CE,
设BE=x,则C'E=CE=4-x,
在Rt△BEC'中,BE2+BC'2=C'E2,
x2+22=(4-x)2,
解得x=32,
即BE=32,CE=4-32=52,
连接EE',如图所示:
由平移的性质得:E'E=BC'=2,EE'//AB//CD,D'E'//DE,
∴△FEE'∽△FCD'∽△ECD,
∴EFEE'=CECD=525=12,
∴EF=12EE'=1;
(3)如图3.1,当AEC'共线时,过点D作DM⊥BC交CB的延长线于点M,
由(2)得:BC=2,C'E=52BE=92
由旋转的性质得:∠DEB=90°,
∴DE//CM,BE//DM,
∴四边形BEDM是平行四边形,
∴DM=BC=2,BM=C'D=5,
∴CM=9,
∴CD= DM2+CM2= 85;
如图3.2,当AC'E共线时,过点D作DN⊥BC交BC的延长线于点N,则DN=BC'=2,BN=CD=5,
∴CN=1,
∴CD= DN2+CN2= 5;
综上所述,CD的长为 85或 5.
(1)由矩形的性质得∠A=90°,AB=CD=5,BC=AD=4,再由折叠的性质得C'D=CD=5,然后由勾股定理求解即可;
(2)由折叠的性质得C'E=CE,设BE=x,则C'E=CE=4-x,在Rt△BEC'中,由BE2+BC'2=C'E2求出BE=32,CE=52,连接EE',根据相似三角形的判定可得△FEE'∽△FCD'∽△ECD,即可求解;
(3)分两种情况讨论:当AEC'共线时,当AC'E共线时,结合勾股定理即可求解.
本题属于四边形综合题,主要考查了矩形与折叠问题,勾股定理,相似三角形的判定和性质,图形的平移问题等,熟练掌握矩形的性质,勾股定理,相似三角形的判定和性质是解题的关键.课题
测量某建筑物AB的高度.
测量工具
皮尺,旗杆等.
设计方案
如图,建筑物AB正前方有一根高度是17米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角为45°旗杆底端D到大楼前梯形底边的距离DC是20米,梯形坡长BC是9米,梯形坡度i=2:、5.注:坡度是9米,梯形坡度i=2:、5,注:坡度=摄高胺底长结果精确到0.1米,参考数据:结果精确到0.1米,参考数据; 5=2.236.
是9米,梯形坡度i=2:、5.注:坡度是9米,梯形坡度i=2:、5,注:坡度=摄高胺底长
河南省信阳市息县2024届九年级下学期中考适应性测试(四)数学试卷(含答案): 这是一份河南省信阳市息县2024届九年级下学期中考适应性测试(四)数学试卷(含答案),共12页。
2023-2024学年河南省信阳市息县培优联盟校九年级(上)适应性数学试卷(一)(含解析): 这是一份2023-2024学年河南省信阳市息县培优联盟校九年级(上)适应性数学试卷(一)(含解析),文件包含人教版一年级数学期末综合复习卷pdf、人教版一年级数学期末综合复习卷答案pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
河南省信阳市息县2022-2023学年八年级下学期适应性测试(一)数学试卷(含解析): 这是一份河南省信阳市息县2022-2023学年八年级下学期适应性测试(一)数学试卷(含解析),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












